
- •Математика и информатика
- •1. Тема: Предел функции. 3
- •1. Тема: Предел функции.
- •Второй замечательный предел. Число e
- •1. Тема: Производная функции.
- •4. Краткие сведения из теоретического курса
- •1. Тема: Дифференциал функции.
- •4. Основные сведения из теоретического курса
- •1. Тема: Производные и дифференциалы высших порядков
- •6. Задание на дом.
- •6.1. Практика:
- •1. Тема: Применение производных к исследованию функций
- •4. Основные сведения из теоретического курса
- •1. Тема: Производные и дифференциалы функции нескольких аргументов. Приложение полного дифференциала функции
- •Частные производные второго порядка
- •5. Самостоятельная работа студентов на занятии.
- •1. Тема: Неопределенный интеграл и его основные свойства. Основные методы интегрирования.
- •Основные понятия
- •Свойства неопределенного интеграла
- •Метод непосредственного интегрирования
- •Свойство инвариантности неопределенного интеграл
- •Метод замены переменной (подстановки)
- •6. Задание на дом.
- •1. Тема: Определенный интеграл и его основные свойства.
- •Свойства определенного интеграла
- •Геометрический смысл определенного интеграла
- •Формула Ньютона-Лейбница
- •Метод замены переменных в определенном интеграле
- •1. Тема: Приложения определенного интеграла.
- •Задача о площади криволинейной трапеции
- •Работа переменной силы
- •Приближенное вычисление определенного интеграла. Формула прямоугольников
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Обыкновенные дифференциальные уравнения. Дифференциальные уравнения первого порядка с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка
- •Дифференциальные уравнения с разделяющимися переменными
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами и их решение
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Применение дифференциальных уравнений для решения прикладных задач
- •5. Самостоятельная работа студентов на занятии
- •6. Задание на дом.
- •1. Тема: Знакомство с персональным компьютером. Основные приемы работы с операционной системой Windows
- •1. Оперативное запоминающее устройство (оперативная память)
- •2. Быстродействие эвм
- •3. Характеристики внешней памяти (внешнее запоминающее устройство - взу)
- •4. Характеристики монитора
- •5. Тип интерфейса и возможности расширения конфигурации технических средств
- •Периферийные устройства
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Контрольная работа
- •1. Тема: Работа с программой графической обработки данных.
- •4. Краткие сведения из теоретического курса
- •Базовое (системное) и прикладное программное обеспечение
- •6. Задание на дом
- •1. Тема: Работа с текстовым редактором ms Word.
- •4. Краткие сведения из теоретического курса
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Работа с электронными таблицами. Ms Excel.
- •4. Краткие сведения из теоретического курса
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Базы данных. Компьютерные сети.
- •4. Краткие сведения из теоретического курса
- •Компьютерные сети
- •Интернет
- •Электронная почта
- •Протокол ftp
- •Www (World Wide Web) – всемирная путина
- •5. Самостоятельная работа студентов на занятии
- •Библиографический список
- •Математика и информатика
- •Часть I
1. Тема: Применение производных к исследованию функций
2. Актуальность темы: Данный раздел математики имеет широкое применение в естественных дисциплинах при построении и анализе различных зависимостей, а также при решении оптимизационных задач.
3. Цель занятия: Выработать навыки исследования функциональных зависимостей и построения графиков функций на основании проведенных исследований.
3.1 Целевые задачи:
знать: необходимое и достаточное условия возрастания (убывания) функции на интервале; необходимое и достаточное условия существования экстремума дифференцируемой функции, схему исследования функции; правило нахождения наибольшего и наименьшего значений функции на отрезке.
уметь: исследовать функцию с помощью производной первого порядка, строить график функции на основании проведенного исследовании, применять производные при решении задач оптимизации.
4. Основные сведения из теоретического курса
Функция называется
возрастающей
(убывающей)
на интервале (a;
b),
если для любых двух точек x1
и x2
из указанного интервала, удовлетворяющих
неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство![]() (
(
![]() ).
).
Необходимое условие возрастания (убывания): Если дифференцируемая функция на интервале (a, b) возрастает (убывает), то производная этой функции неотрицательна (неположительна) в этом интервале f’(x)0 (f’(x)≤0).
Достаточное условие возрастания (убывания): Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого интервала, то функция возрастает (убывает) на этом интервале.
Функция f(x) в точке х1 имеет максимум, если для любого х из некоторой окрестности точки выполняется неравенство: f(x1)>f(x), при xx1.
Функция f(x) в точке х1 имеет минимум, если для любого х из некоторой окрестности точки выполняется неравенство: f(x1)<f(x), при xx1.
Экстремум функции называют локальным экстремумом, так как понятие экстремума связано лишь с достаточно малой окрестностью точки х1. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой. Наличие максимума или минимума в отдельной точке интервала не означает, что в этой точке функция f(x) принимает наибольшее или наименьшее значение на этом интервале.
Необходимое условие экстремума: В точке экстремума дифференцируемой функции ее производная равна нулю.
Достаточное условие экстремума: Если производная дифференцируемой функция в некоторой точке х0 равна нулю и меняет свой знак при переходе через это значение, то число f(х0) является экстремумом функции, причем если изменение знака происходит с плюса на минус, то максимум, если с минуса на плюс, то минимум.
Точки, в которых производная непрерывной функции равна нулю или не существует называются критическими.
Углы наклона касательных к кривой у=f(x) меняются с острых на тупые при переходе через точку максимума и с тупых на острые при переходе через точку минимума.
Исследовать функцию на экстремум означает найти все ее экстремумы. Правило исследования функции на экстремум:
Найти критические точки функции у = f(x) и выбрать из них лишь те, которые являются внутренними точками области определения функции;
Исследовать знак производной f'(x) слева и справа от каждой из выбранных критических точек;
В соответствии с достаточным условие экстремума выписать точки экстремума (если они есть) и вычислить значения функции в них.
Для того чтобы найти наибольшее и наименьшее значение функции на отрезке необходимо выполнить несколько этапов:
Найти критические токи функции, решив уравнение f’(x)=0.
Если критические точки попали на отрезок, то необходимо найти значения в критических точках и на границах интервала. Если критические точки не попали на отрезок (или их не существует), то находят значения функции только на границах отрезка.
Из полученных значений функции выбирают наибольшее и наименьшее и записывают ответ, например, в виде:
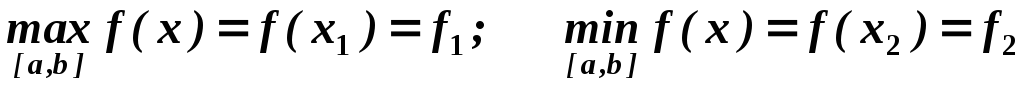 .
.
Решение задач.
Исследовать функцию на экстремум
1.
![]() .
.
2.
![]() .
.
3. Исследовать
функцию
![]() и построить ее график.
и построить ее график.
4. Найти наименьшее
и наибольшее значения функции
![]() на отрезке
на отрезке![]() .
.
5. Самостоятельная работа студентов на занятии.
5.1.Исследовать
функцию
![]() и построить ее график.
и построить ее график.
5.2. Исследовать
функцию
![]() на экстремум.
на экстремум.
5.3. Найти наибольшее
и наименьшее значения функции
![]() на отрезке
на отрезке![]() .
.
5.4. Найти интервалы возрастания и убывания функции, точки максимума и минимума и точки пересечения с осями:
1.
![]() .
.
2.
![]() .
.
6. Задание на дом.
6.1. Практика:
6.1.1. Найти наибольшее
и наименьшее значения функции
![]() на отрезке а)
на отрезке а)![]() ;
б)
;
б)![]() .
.
6.1.2. Найти интервалы возрастания и убывания функций:
1)
![]() .
.
2)![]() .
.
6.1.3. Исследовать
и построить график функции
![]() .
.
6.2. Теория.
6.2.1. Лекция по теме «Производные и дифференциалы функции нескольких аргументов. Приложение дифференциала функции нескольких аргументов».
6.2.2. Лобоцкая Н. Л. и др. С. 71-77.
6.2.3. Казуб В.Т. , Воронина С.В. и др. Основы математического анализа. С 71-83.
6.2.4. Казуб В.Т., Воронина С.В. Математический анализ. Дифференциальные уравнения. С. 37-50.
