
- •Математика и информатика
- •1. Тема: Предел функции. 3
- •1. Тема: Предел функции.
- •Второй замечательный предел. Число e
- •1. Тема: Производная функции.
- •4. Краткие сведения из теоретического курса
- •1. Тема: Дифференциал функции.
- •4. Основные сведения из теоретического курса
- •1. Тема: Производные и дифференциалы высших порядков
- •6. Задание на дом.
- •6.1. Практика:
- •1. Тема: Применение производных к исследованию функций
- •4. Основные сведения из теоретического курса
- •1. Тема: Производные и дифференциалы функции нескольких аргументов. Приложение полного дифференциала функции
- •Частные производные второго порядка
- •5. Самостоятельная работа студентов на занятии.
- •1. Тема: Неопределенный интеграл и его основные свойства. Основные методы интегрирования.
- •Основные понятия
- •Свойства неопределенного интеграла
- •Метод непосредственного интегрирования
- •Свойство инвариантности неопределенного интеграл
- •Метод замены переменной (подстановки)
- •6. Задание на дом.
- •1. Тема: Определенный интеграл и его основные свойства.
- •Свойства определенного интеграла
- •Геометрический смысл определенного интеграла
- •Формула Ньютона-Лейбница
- •Метод замены переменных в определенном интеграле
- •1. Тема: Приложения определенного интеграла.
- •Задача о площади криволинейной трапеции
- •Работа переменной силы
- •Приближенное вычисление определенного интеграла. Формула прямоугольников
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Обыкновенные дифференциальные уравнения. Дифференциальные уравнения первого порядка с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка
- •Дифференциальные уравнения с разделяющимися переменными
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами и их решение
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Применение дифференциальных уравнений для решения прикладных задач
- •5. Самостоятельная работа студентов на занятии
- •6. Задание на дом.
- •1. Тема: Знакомство с персональным компьютером. Основные приемы работы с операционной системой Windows
- •1. Оперативное запоминающее устройство (оперативная память)
- •2. Быстродействие эвм
- •3. Характеристики внешней памяти (внешнее запоминающее устройство - взу)
- •4. Характеристики монитора
- •5. Тип интерфейса и возможности расширения конфигурации технических средств
- •Периферийные устройства
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Контрольная работа
- •1. Тема: Работа с программой графической обработки данных.
- •4. Краткие сведения из теоретического курса
- •Базовое (системное) и прикладное программное обеспечение
- •6. Задание на дом
- •1. Тема: Работа с текстовым редактором ms Word.
- •4. Краткие сведения из теоретического курса
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Работа с электронными таблицами. Ms Excel.
- •4. Краткие сведения из теоретического курса
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Базы данных. Компьютерные сети.
- •4. Краткие сведения из теоретического курса
- •Компьютерные сети
- •Интернет
- •Электронная почта
- •Протокол ftp
- •Www (World Wide Web) – всемирная путина
- •5. Самостоятельная работа студентов на занятии
- •Библиографический список
- •Математика и информатика
- •Часть I
Свойства определенного интеграла
Определенный интеграл не зависит от обозначения переменной интегрирования:
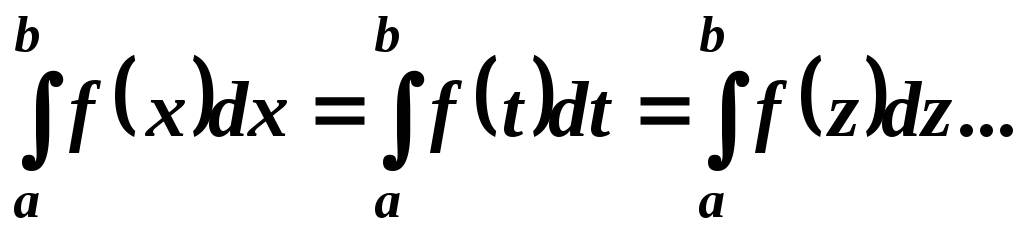
Определенный интеграл с одинаковыми пределами равен нулю:
 .
.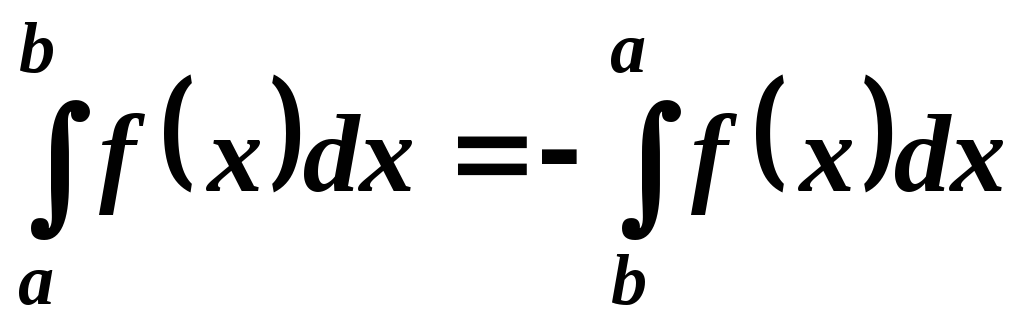 .
. при
при
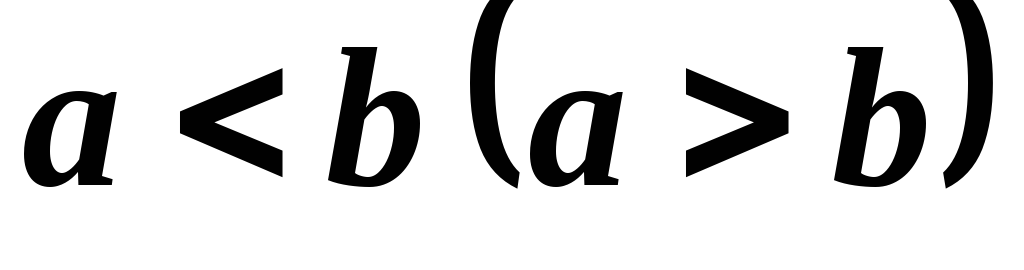 .
.Если с – постоянное число и функция f(x) интегрируема на отрезке [a, b], то
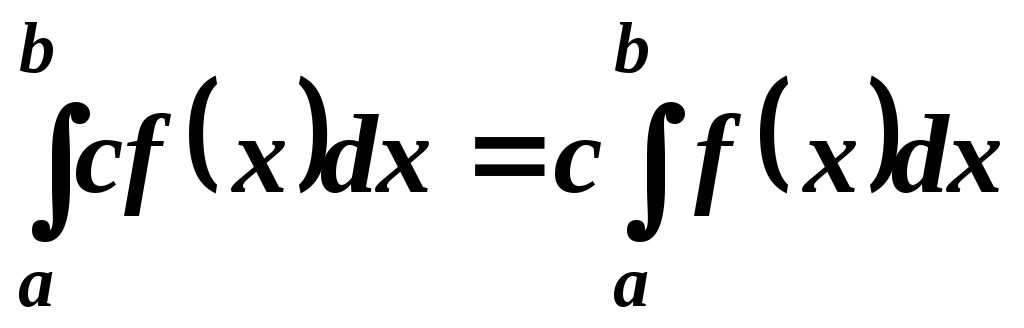 ,
т. е. постоянный
множитель с
можно вынести за знак определенного
интеграла.
,
т. е. постоянный
множитель с
можно вынести за знак определенного
интеграла.Если функции f1(x) и f2(x) интегрируемы на [a, b], тогда
![]() ,
т. е. интеграл от суммы равен сумме
интегралов.
,
т. е. интеграл от суммы равен сумме
интегралов.
Свойство аддитивности. Если f(x) интегрируема на отрезке [a, b] и a<c<b, то
 ,т.
е.
интеграл по всему отрезку равен сумме
интегралов по частям этого отрезка.
,т.
е.
интеграл по всему отрезку равен сумме
интегралов по частям этого отрезка.
8.
Если
на отрезке [а,
b],
где а<b,
f(x) ≤ g(x),
mo
u
![]() ,
т.е.
обе части неравенства можно почленно
интегрировать.
,
т.е.
обе части неравенства можно почленно
интегрировать.
9.
Пусть
на отрезке [а,
b],
где a<b,
т≤
f(x)≤M,
где
т
и М – некоторые
числа. Тогда
![]() .
.
10. (Теорема о среднем). Если функция y=f(x) непрерывна на отрезке [а, b], (где а < b), то найдется такое значение c[a, b], что
![]() или
или
 .
.
Геометрический смысл определенного интеграла
Пусть на отрезке [a, b] задана непрерывная функция y=f(x)0. Фигура ограниченная сверху графиком функции, снизу – осью Ох, сбоку – прямыми х=а, х=b, называется криволинейной трапецией.
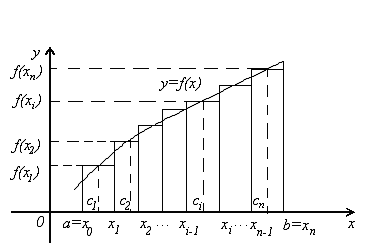
Рассмотрим функцию
y=f(x),
которая определена на отрезке [a,
b].
Разобьем
отрезок [a,
b] точками
а=х0,х1…,хn=b
(х0<х1<…<хn)
на
n
частичных отрезков, в каждом из которых
возьмем произвольную точку
сi.
Умножим f(ci)
на длину соответствующего частичного
отрезка xi.
Сумма всех таких произведений
![]() равна площади ступенчатой фигуры и
приближенно равна площади криволинейной
трапеции
равна площади ступенчатой фигуры и
приближенно равна площади криволинейной
трапеции![]() .
За точное значение площади криволинейной
трапеции принимают предел
S, к которому
стремится площадь ступенчатой фигуры
Sn,
когда n
стремится
к :
.
За точное значение площади криволинейной
трапеции принимают предел
S, к которому
стремится площадь ступенчатой фигуры
Sn,
когда n
стремится
к :
![]() .
.
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
Формула Ньютона-Лейбница
Теорема.
Если функция
y=f(x)
непрерывна на отрезке [a,b]
и F(x) –
какая-либо ее первообразная на [a,b]
(F’(x)=f(x)),
то имеет место формула:
![]() .Данное
равенство называется формулой
Ньютона-Лейбница.
.Данное
равенство называется формулой
Ньютона-Лейбница.
Понятие определенного интеграла с переменным верхним пределом
Если
функция y=f(x)
интегрируема
на отрезке [а,
b],
то, очевидно,
она интегрируема также на произвольном
отрезке [а,
х], вложенном
в [а, b].
По определению
![]() ,
где х[а,
b],
а функция Ф(х) называется интегралом с
переменным верхним пределом.
,
где х[а,
b],
а функция Ф(х) называется интегралом с
переменным верхним пределом.
Метод замены переменных в определенном интеграле
Пусть для вычисления
интеграла
![]() от непрерывной функции сделана
подстановка
от непрерывной функции сделана
подстановка![]() .
Если функция
.
Если функция
![]() и
ее производная
и
ее производная![]() непрерывны;()=а,
()=b,
то
непрерывны;()=а,
()=b,
то
![]() .
При вычислении определенного интеграла
методом замены переменных возвращаться
к исходной переменной не требуется,
так как определенный интеграл есть
некоторое постоянное число. Достаточно
лишь найти пределы интегрированияα
и β
по новой переменной t
как решение
относительно переменной t
уравнений
.
При вычислении определенного интеграла
методом замены переменных возвращаться
к исходной переменной не требуется,
так как определенный интеграл есть
некоторое постоянное число. Достаточно
лишь найти пределы интегрированияα
и β
по новой переменной t
как решение
относительно переменной t
уравнений
![]() и
и![]() .
.
Метод интегрирования по частям в определенном интеграле
Если u=u(x)
и
v=v(x)
имеют непрерывные производные на
отрезке [a,b],
то имеет место формула:
![]() .
Эта формула называется формулой
интегрирования по частям для определенного
интеграла.
.
Эта формула называется формулой
интегрирования по частям для определенного
интеграла.
Решение задач
Вычислить определенные интегралы:
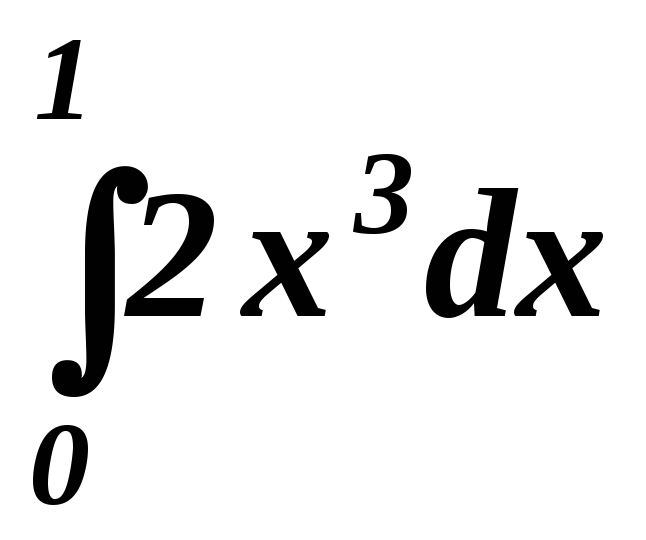 .
.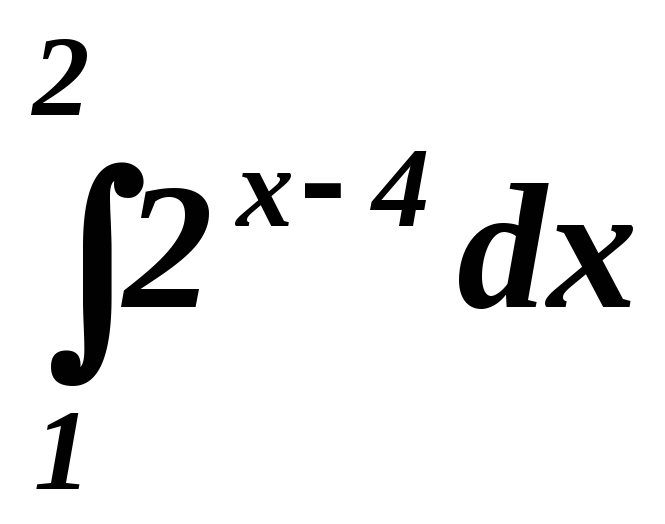 .
.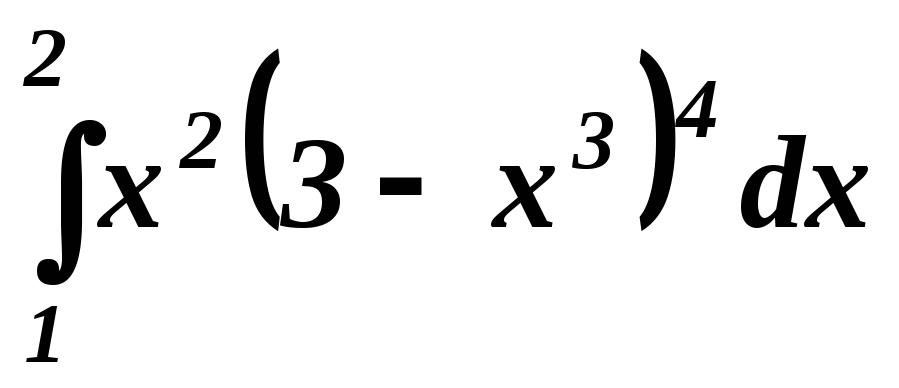 .
. .
.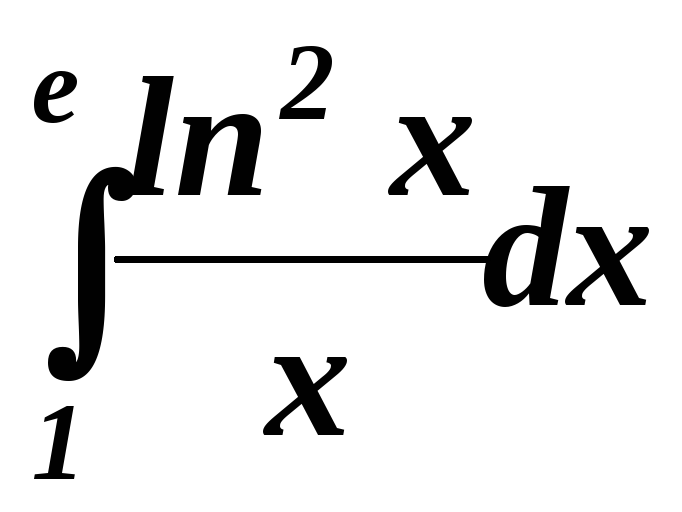 .
.
5. Самостоятельная работа студентов на занятии.
5.1. Найти интегралы:
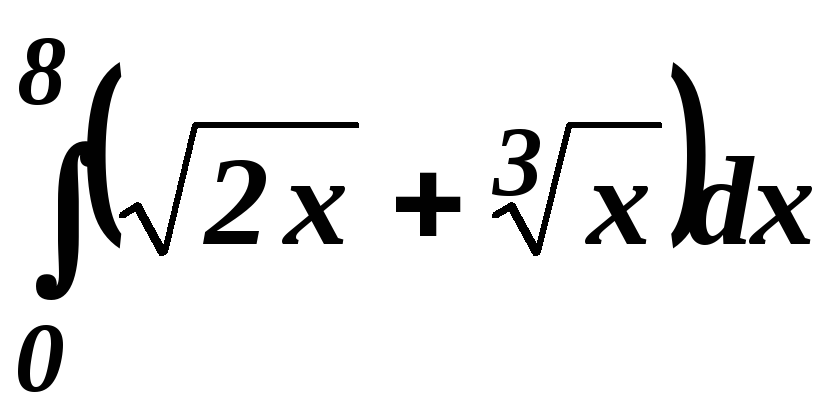 .
. .
.
 ex
cosxdx.
ex
cosxdx.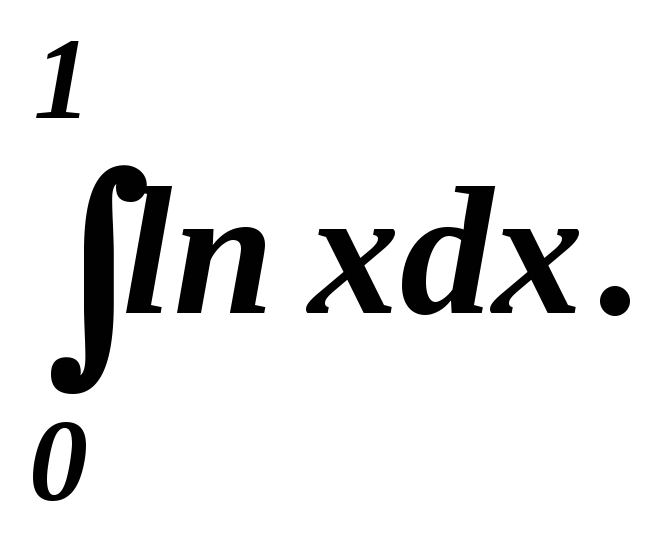
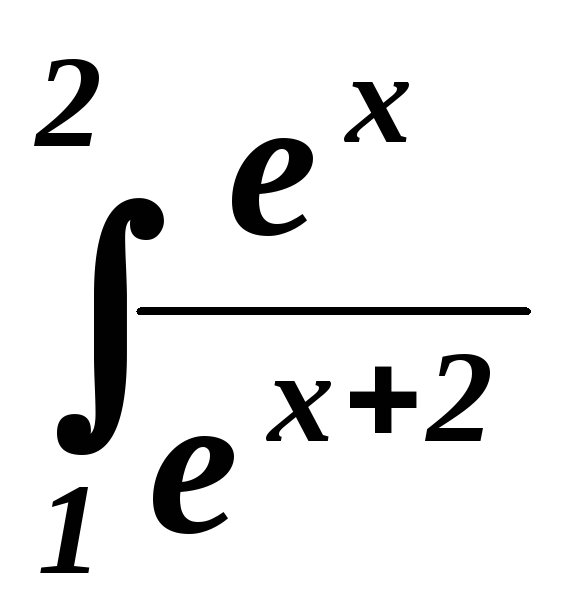 dx.
dx.
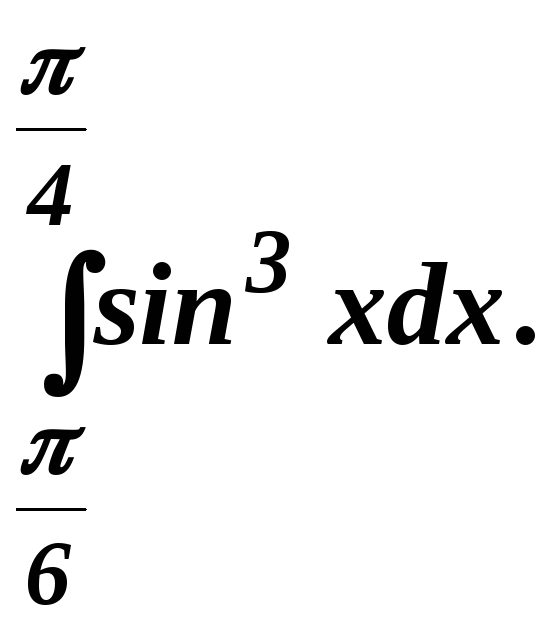
6. Задание на дом.
6.1. Практика:
6.1.1. Вычислить определенные интегралы:
1. ![]() x3
ln
xdx. 3.
x3
ln
xdx. 3. ![]()
2. ![]() dx. 4.
dx. 4. ![]() .
.
6.1.2. Лобоцкая Н.Л. и др. С. 104 № 2, .6, 19, 20
2.
![]() .
.
6.
![]() .
.
19.
![]() .
.
20.
![]() .
.
6.2. Теория.
6.2.1. Лекция по теме «Приложение определенного интеграла».
6.2.2. Лобоцкая Н. Л. и др. С. 99-104.
6.2.3. Казуб В.Т. , Воронина С.В. и др. Основы математического анализа. С 122-130.
6.2.4. Казуб В.Т., Воронина С.В. Математический анализ. Дифференциальные уравнения. С. 70-73.
