5. Самостоятельная работа студентов на занятии.

5.1. Найти все частные производные функций:

1..

2. .

3. .

4. .

5.2. Найти частные и полный дифференциал для следующих функций:

1..

2..

3..

5.3. Найти все частные производные второго порядка функции:

1. .

2..

3. .

4..

5.4. Вычислить приближенно , исходя из значения функцииприх=0 и у=1.

6. Задание на дом.

6.1. Практика:

6.1.1. Найти все частные производные функций:

1. .

2) .

6.1.2. Найти частные и полный дифференциал для следующих функций:

1) .

2) .

3) .

4) .

6.1.3. Лобоцкая Н.Л. и др. С. 78 № 21, 23,24, 26, 30.

21. .

23. .

24. .

26. .

30. .

6.2. Теория.

6.2.1. Лекция по теме «Неопределенный интеграл».

6.2.2. Лобоцкая Н. Л. и др. С. 80-85.

6.2.3. Казуб В.Т. , Воронина С.В. и др. Основы математического анализа. С 84-95.

6.2.4. Казуб В.Т., Воронина С.В. Математический анализ. Дифференциальные уравнения. С. 51-58.

1. Тема: Неопределенный интеграл и его основные свойства. Основные методы интегрирования.

2. Актуальность темы: понятие неопределенного интеграла является одним из ключевых понятий математического анализа. Методы интегрирования позволяют решать задачу восстановления функции по ее производной, которая находит широкое применение в естественнонаучных дисциплинах.

3. Цель занятия: закрепление понятия неопределенного интеграла; овладение способами и методами интегрирования.

3.1 Целевые задачи:

знать: понятие первообразной функции, определение неопределенного интеграла, основные свойства неопределенного интеграла; свойства интеграла; сущность методов интегрирования;

уметь: применять основные формулы интегрирования при нахождении интегралов методом непосредственного интегрирования; использовать свойство инвариантности неопределенного интеграла, применять методы интегрирования.

4. Краткие сведения из теоретического курса

Основные понятия

Восстановление функции по известной производной этой функции основная задача интегрального исчисления (т.е. найти функцию F(x), зная ее производную или дифференциал).

Первообразной функцией для данной функции f(x) на интервале называется такая функция F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx на рассматриваемом интервале.

Теорема. Если функция F(x) является первообразной для функции f(x) на некотором интервале, то множество всех первообразных для f(x) задается формулой F(x)+C, где С – постоянное число:

.

Множество всех первообразных функций F(x)+C для f(x) или f(x)dx называется неопределенным интегралом от функции f(x) и обозначается .Таким образом можно записать , еслиF’(x)=f(x).

Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции, т. е. .

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. .

3. Интеграл от дифференциала первообразной равен самой первообразной и дополнительному слагаемому С, т. е.

4. Постоянный множитель не равный нулю можно вынести за знак неопределенного интеграла, т. е.

5. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых, т. е.

.

Таблица простейших интегралов

1. ;

2. ;

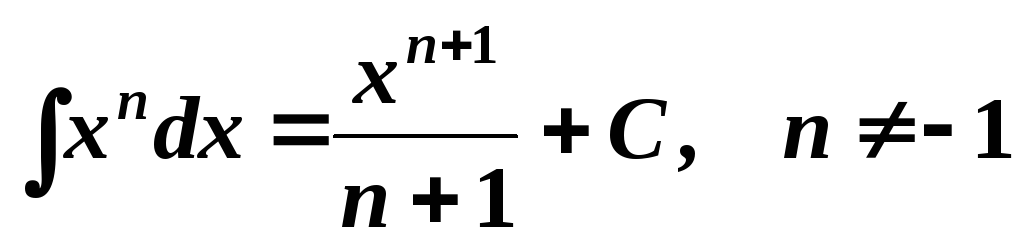3. , при ;

4. , ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

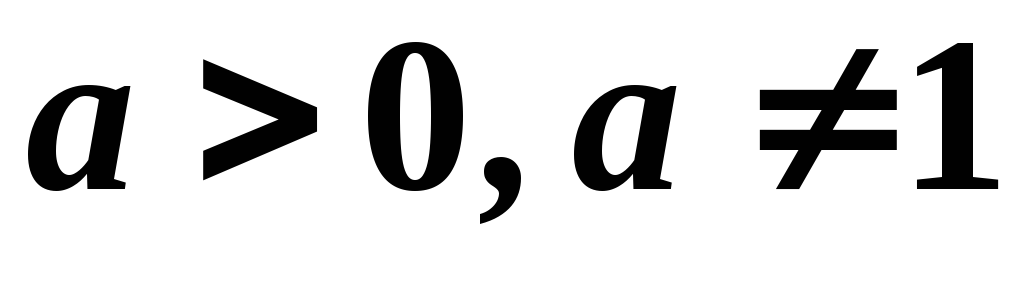Вывести данные формулы можно, пользуясь тем, что интегрирование – это операция обратная дифференцированию. Если dF(x)=f(x)dx, то .

Например, .