1. Тема: Дифференциал функции.

2. Актуальность темы: Дифференциал функции используется при приближенных вычислениях приращений функции и значений функции.

3. Цель занятия: Выработать навыки нахождения дифференциала функции одной переменной и решения прикладных задач.

3.1 Целевые задачи:

знать: понятие дифференциала функции, геометрический и аналитический смысл дифференциала, свойства дифференциала, формулы приближенных вычислений.

уметь: находить дифференциалы функций одной переменной, использовать свойства дифференциалов, вычислять приближенно значения функций и приращений функций.

4. Основные сведения из теоретического курса

Дифференциал функции равен произведению производной этой функции на дифференциал аргумента: .

Аналитический смысл дифференциала функции: заключается в том, что дифференциал функции, есть главная часть приращения функции f. Дифференциал функции отличается от приращения функции на бесконечно малую более высокого порядка малости, чем x. Действительно, или.

Свойства дифференциала функции:

1) дифференциал постоянной: ;

2) дифференциал суммы. ;

3) дифференциал произведения. ;

4) дифференциал частного. ;

5) дифференциал сложной функции. Дифференциал сложной функции (функции от функции) равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента(при условии, что обе функции дифференцируемы): , гдеи функции– дифференцируемые функции своего аргумента.

Геометрический смысл дифференциала функции:

Дифференциал функции y=f(x) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение Δх (рис. 3.1).

Рис. 3.1

Равенство позволяет с большой точностью вычислять приближенно приращение любой дифференцируемой функции; формулаиспользуется для вычисления приближенных значений функций.

Решение задач

1. Найти дифференциал функции:

а); б)..

2. Вычислить приближенно .

3. Пусть . Найтиy и dy при значении х=1 и сравнить их между собой, если а) =1; б) =0,1; в) =0,01.

5. Самостоятельная работа студентов на занятии.

5.1.Найти дифференциалы следующих функции:

1. ;

2. ;

3. ;

4. ;

5. 

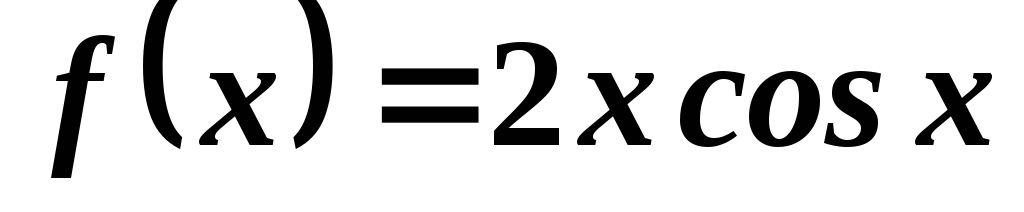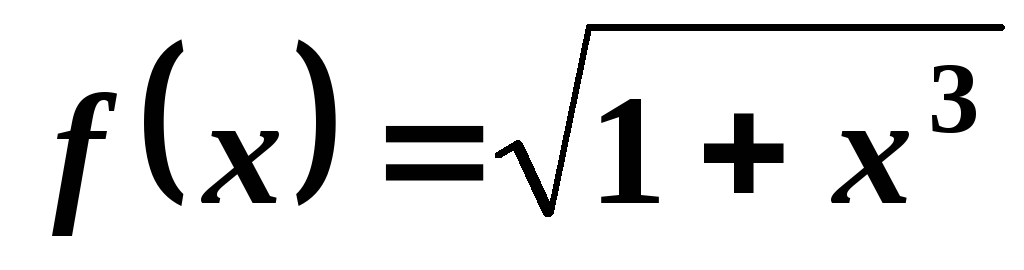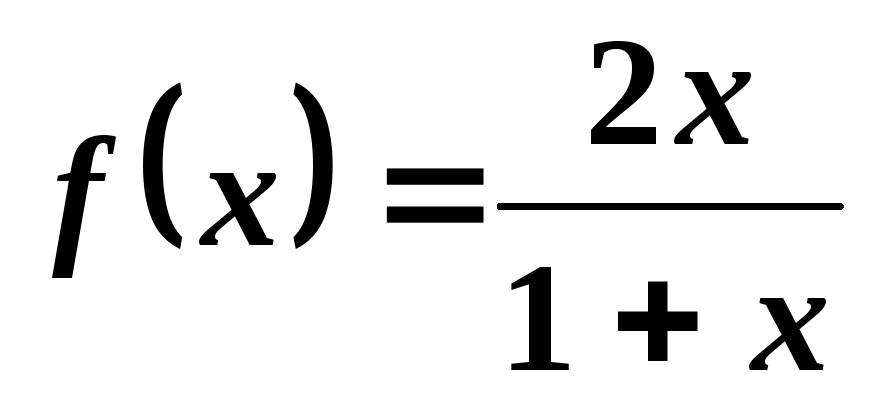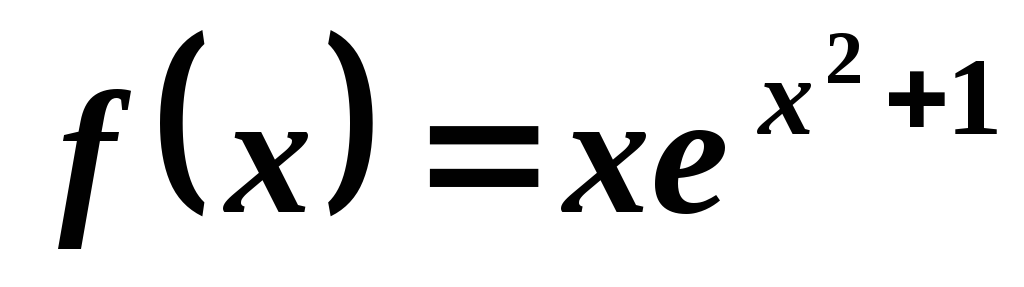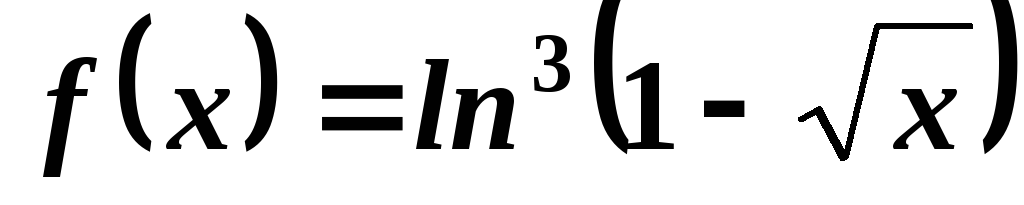
5.2. Используя понятие дифференциала, вычислить:

1. ;

2. ;

3. ;

4. .

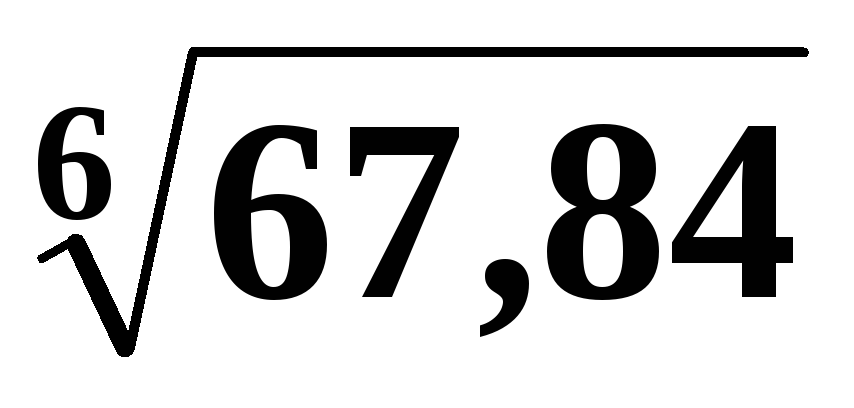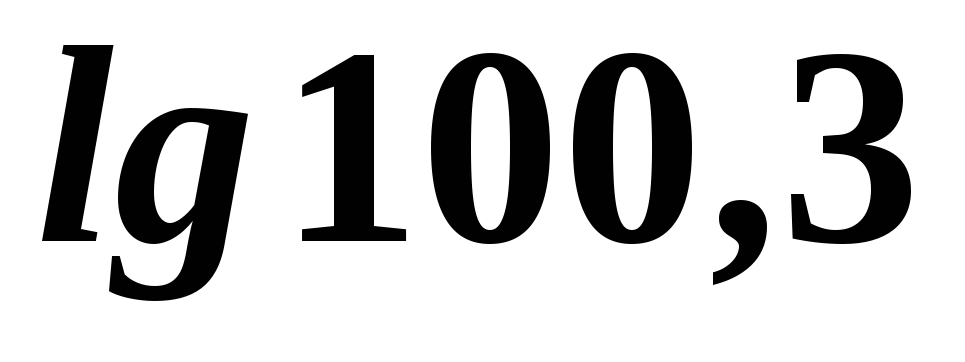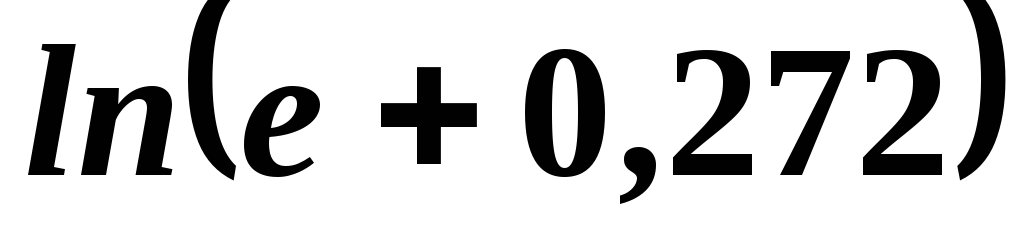6. Задание на дом.

6.1. Практика:

6.1.1. Найти дифференциал функции:

1. ;

2. ;

3. .

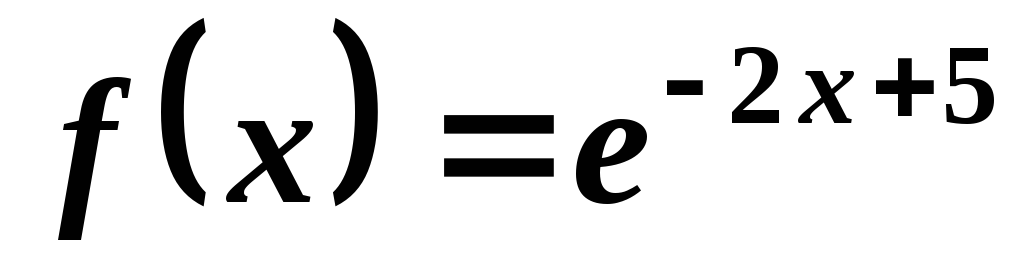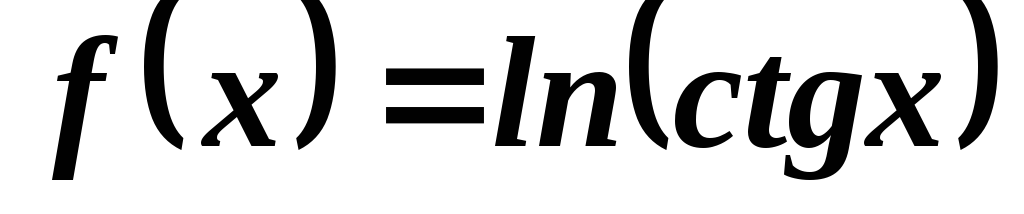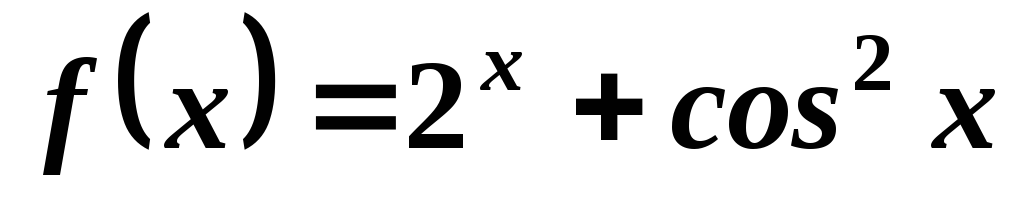6.1.2. Вычислить приближенно:

4. ;

5. .

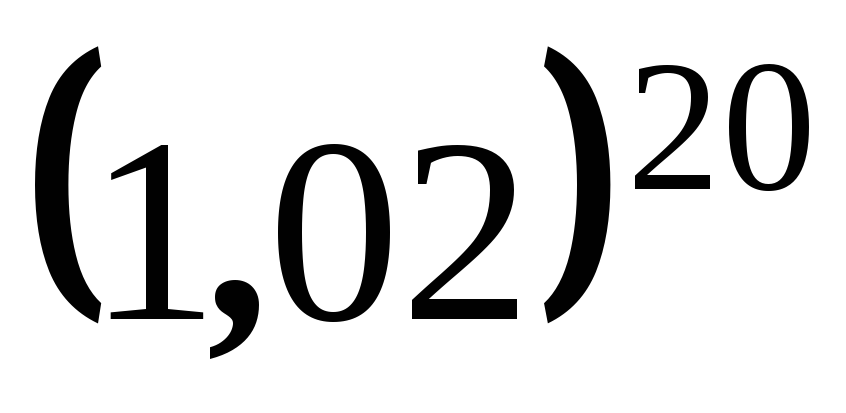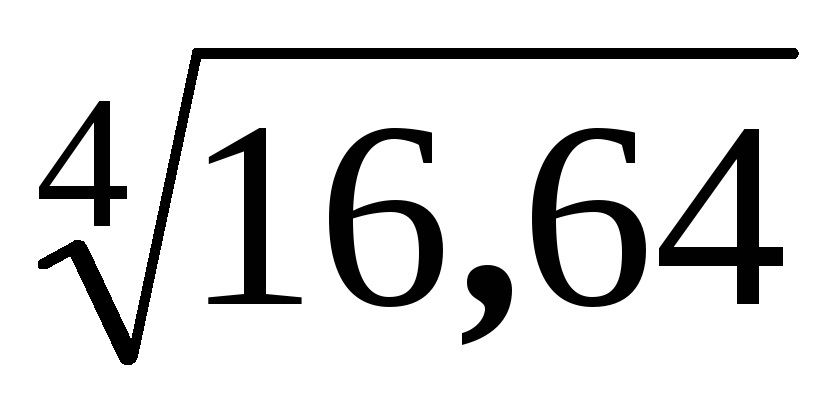6.1.3. Лобоцкая Н. Л. и др. С.56 №№ 85-88.

85.;

86.;

87.;

88. .

6.2. Теория.

6.2.1. Лекция по теме «Производные и дифференциалы высших порядков».

6.2.2. Лобоцкая Н. Л. и др. С. 46, 49.

6.2.3. Казуб В.Т. , Воронина С.В. и др. Основы математического анализа. Учебно-методическое пособие для студентов I курса специальности «Фармация»// Пятигорск: Пятиг. гос.-фармац. акад., 2006. С 63-69.

6.2.4. Казуб В.Т., Воронина С.В. Математический анализ. Дифференциальные уравнения: учебно-методическое пособие для студентов I курса специальности «Фармация» »// Пятигорск: Пятиг. гос.-фармац. акад., 2006. С. 27-31