
Объёмно-пространственная композиция
.pdf
Глава 5. Ритм |
71 |

72 Часть II. Средства архитектурной кожпозици
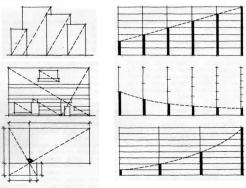
Рис. 88. Учебная |
терьерного про- |
композиция. Ритм |
странства |
в построении ин- |
|
бенно в процессе создания проек тов и осмысления итогов реализо ванных художественных замыслов в натуре.
Контрольные вопросы
1.Почему метроритмические закономер ности получают широкое распространение в построении художественных форм в искусст ве н, в частности, в архитектуре?
2.Приведите примеры удачного исполь зовании ритма в современной архитектуре. Проиллюстрируйте особенности атих ритми ческих форм на схемах или объемных моде-
3.Какие новые формы ритма получают распространение в построении архитектур ных ансамблей?
4.В решении сложной фронтальной композиции проанализируйте связь метро ритмических построений в силуэте и харак тере поверхности.
5.Предложите конкретные способы пре одоления возможного однообразия от повтор ности элементов архитектурной формы. Най дите удачные, на Ваш взгляд, примеры разрешения подобной задачи в практике современной архитектуры.
в.Ритмы изогнутых линий и поверхно стей. Покажите яркие образцы архитектур ных композиций, ритмы которых не облада ют отчетливыми признаками ряда.
7. Почему в ансамблевых построениях особенно возрастает роль ритмических свя зей? Как конкретно проявляются простран ственные формы ритма?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глаза 6. Пропорции |
|
|
73 |
||||||
|
|
|
ГЛАВА 6*. ПРОПОРЦИИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
6.1. Понятие о пропорции в бо перпендикулярны (обратная про |
|||||||||||||||||||||||
архитектуре. Одним |
из |
важнейших |
порция) (рис.89 — 91). Пропорцию, |
|||||||||||||||||||||||
методов построения |
выразительной |
средние члены которой равны меж |
||||||||||||||||||||||||
и целостной |
архитектурной |
формы |
ду |
собой, |
|
называют |
|
непрерывной. |
||||||||||||||||||
является пропорционирование. |
|
Примером |
непрерывной |
|
пропорции |
|||||||||||||||||||||
|
Пропорция (лат. ргорогНо) — со |
может служить ряд подобных пря |
||||||||||||||||||||||||
размерность, |
определенное |
соотно |
моугольников, |
в |
котором |
|
длина |
|||||||||||||||||||
шение частей между собой. В совре |
предыдущего |
прямоугольника |
рав |
|||||||||||||||||||||||
менной литературе понятие пропор |
на ширине последующего. |
|
|
|
||||||||||||||||||||||
ции употребляется в трех основ |
ке, |
Здесь, так же как и в математи |
||||||||||||||||||||||||
ных, |
|
частично |
перекрывающих |
различают |
два |
вида |
отноше |
|||||||||||||||||||
друг друга значениях. |
|
|
|
|
ний |
— |
рациональные, |
|
|
|
|
|
|
|||||||||||||
|
Первое — |
наиболее |
|
близкое к |
|
которые |
могут быть |
|
выражены |
|||||||||||||||||
понятию соразмерности — означает |
каким-либо конечным целым или |
|||||||||||||||||||||||||
соотношение |
основных |
параметров |
дробным |
числом, |
и |
|
иррациональ |
|||||||||||||||||||
формы (длина, ширина, высота). |
ные, которые не могут быть выра |
|||||||||||||||||||||||||
Именно это значение имеют в виду, |
жены |
конечным |
числом |
(например, |
||||||||||||||||||||||
когда говорят о пропорциях какой- |
2, |
3, |
5 и т.д.). |
|
|
|
|
|
|
|
|
|||||||||||||||
либо |
отдельно. взятой |
вещи |
(зда |
|
Однако, если в математике под |
|||||||||||||||||||||
ния, картины, книги и др.). Про |
отношением |
понимают |
частное |
от |
||||||||||||||||||||||
порция |
здесь |
характеризует |
объект |
деления одной величины на дру |
||||||||||||||||||||||
как целое, составляет основу его об |
гую, то понятие отношения в архи |
|||||||||||||||||||||||||
раза. Так, одно только соотношение |
тектуре гораздо шире и включает в |
|||||||||||||||||||||||||
параметров формы по трем коорди |
себя все виды взаимосвязи вели |
|||||||||||||||||||||||||
натам |
уже |
способно |
создать |
об |
чин, |
характеризующих |
|
объектив |
||||||||||||||||||
раз |
|
спокойствия |
и |
статичности |
ные свойства формы. Поэтому в |
|||||||||||||||||||||
(куб), |
|
динамики |
|
(вытянутая |
третьем и наиболее правильном на |
|||||||||||||||||||||
призма) и др. |
|
|
|
|
|
|
наш взгляд случае под пропорцией |
|||||||||||||||||||
|
Во втором значении под пропор |
в архитектуре понимают любую за |
||||||||||||||||||||||||
цией в архитектуре (так же как и в |
кономерность в соотношениях вели |
|||||||||||||||||||||||||
математике) |
понимают |
равенство |
чин, |
которая связывает |
отдельные |
|||||||||||||||||||||
отношений |
|
количественной |
меры |
части и параметры формы в единое |
||||||||||||||||||||||
одних и тех же объективных |
целое. Таким образом, пропорция в |
|||||||||||||||||||||||||
свойств |
в |
сопоставляемых |
формах |
архитектуре |
есть понятие, |
отража |
||||||||||||||||||||
или их частях и в математической |
ющее |
|
однородность |
|
(закономер |
|||||||||||||||||||||
форме |
записывают |
как |
а/в |
= |
с/б.. |
ность) |
изменений |
количественной |
||||||||||||||||||
Это |
значение |
понятия |
"пропорция" |
меры при переходах от одной части |
||||||||||||||||||||||
используется |
в |
подавляющем боль |
формы к другой и к форме в целом. |
|||||||||||||||||||||||
шинстве работ, посвященных про- |
Легко заметить, что первое и вто |
|||||||||||||||||||||||||
порционированию |
в архитектуре. |
рое определения пропорции явля |
||||||||||||||||||||||||
Из |
математической |
записи |
такого |
ются |
частными |
случаями |
последне |
|||||||||||||||||||
понимания |
пропорции |
следует, |
что |
го определения. |
|
|
|
|
|
|
|
|
||||||||||||||
здесь |
в |
основе |
образования |
целост |
|
6.2. Виды пропорциональных |
от |
|||||||||||||||||||
ной формы лежит принцип |
геомет |
ношений. В |
теории |
и |
практике |
ар |
||||||||||||||||||||
рического |
подобия. |
Наиболее |
рас |
|||||||||||||||||||||||
хитектуры |
хорошо |
известны |
такие |
|||||||||||||||||||||||
пространенным |
в архитектуре |
при |
||||||||||||||||||||||||
виды |
закономерных |
(однородных) |
||||||||||||||||||||||||
мером |
применения |
пропорции |
как |
|||||||||||||||||||||||
изменений |
величин, |
как арифмети |
||||||||||||||||||||||||
равенства |
математических отноше |
|||||||||||||||||||||||||
ческая |
гармоническая |
и |
геометри |
|||||||||||||||||||||||
ний |
является |
образование |
формы |
|||||||||||||||||||||||
ческая |
прогрессии. |
|
|
|
|
|
|
|
||||||||||||||||||
на |
основе |
подобных |
прямоугольни |
|
|
|
|
|
|
|
||||||||||||||||
|
Арифметическая |
прогрессия |
|
вы |
||||||||||||||||||||||
ков, |
диагонали |
которых |
либо |
па |
|
|
||||||||||||||||||||
ражается |
рядом |
чисел, |
|
в |
котором |
|||||||||||||||||||||
раллельны |
(прямая пропорция), ли |
|
||||||||||||||||||||||||
каждое |
последующее |
число |
больше |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
74 Часть II. Средства архитектурной композиции
предыдущего на одну и ту же вели чину. Простейшим примером ариф
метической |
прогрессии является |
ряд целых |
натуральных чисел |
О, 1, 2, 3, 4, 5 и т.д., образом кото рого может служить обычная мер ная линейка. По мере возрастания ряда отношения (математические) между соседними членами развива ются от контрастных к нюансным, приближаясь в пределе к равенству (сравните, например, 1/2 и 999/1000).
Гармоническая прогрессия — это ряд чисел обратных ряду чисел арифметической прогрессии, напри мер: 1/2, 1/3, 1/4, 1/5, 1/6, 1/7. Она лежит в основе музыкального строя, так как всю музыкальную гамму можно получить, прижимая струну в точках, отстоящих от кон ца на рациональное кратное перво начальной ее длине. Отношения (математические) между соседними членами гармонического ряда по
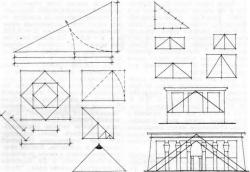
Рис. |
89. |
Компози |
Рис. |
91. |
Виды про |
|
ция, |
построенная |
порций на основе по |
||||
из подобных прямо |
добных |
прямоуголъ- |
||||
угольников |
|
|
|
|||
Рис. |
90. |
Принцип |
|
|
|
|
геометрического по |
Рис. |
92. |
Основные |
|||
добия |
в |
композиции |
||||
виды |
рядов |
|||||
фасада |
|
|||||
|
|
|
|
|||
мере его возрастания так же, как и в арифметической прогрессии, из меняются от контрастных к нюанс ным (рис.92).
Геометрическая прогрессия
представляет собой ряд чисел, в ко тором каждое последующее число больше (или меньше) предыдущего в одно и то же число раз. Напри мер: 1, 2, 4, 8, 16, ...: 1, 1/2, 1/4, 1/8, 1/16. Отношение между сосед ними членами геометрического ря да на всем его протяжении остается постоянным, равным знаменателю прогрессии.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 6, Пропорции |
|
75 |
|||||
|
Ряды чисел могут быть получе |
нальной между всем отрезком и |
|||||||||||||||||||||
ны и на основе других, более или |
меньшей частью (рис.93). Если дли |
||||||||||||||||||||||
менее |
сложных |
|
закономерностей. |
ну отрезка принять за единицу, то |
|||||||||||||||||||
Например, существуют ряды, каж |
его части будут выражаться ирра |
||||||||||||||||||||||
дый член которых равен предыду |
циональными |
числами X = |
0,618, |
||||||||||||||||||||
щему, возведенному в какую-либо |
а — х — 0,382. На основе этих чи |
||||||||||||||||||||||
степень (квадрат, куб и т.д.). Одна |
сел может быть получен геометри |
||||||||||||||||||||||
ко |
излишне |
|
контрастные |
отноше |
ческий ряд ... — 0,146 — 0,236 — |
||||||||||||||||||
ния смежных членов таких рядов |
0,382 — |
0,618 — |
1 |
— |
1,618 — |
||||||||||||||||||
препятствуют |
их |
|
применению |
для |
2,618 |
— 4,236 — 6,854 — .... обна |
|||||||||||||||||
гармонизации |
формы. |
|
|
|
|
руживаемый при |
рассмотрении |
са |
|||||||||||||||
|
Широко |
используются |
в |
архи |
мого широкого круга явлений при |
||||||||||||||||||
тектуре |
аддитивные |
ряды, постро |
роды, искусства и архитектуры. Не |
||||||||||||||||||||
енные на суммировании чисел. На |
случайно |
знаменитый |
итальянский |
||||||||||||||||||||
пример, в ряде чисел 1, 2, 3, |
|
5, 8, |
философ и математик Фра Лука |
||||||||||||||||||||
13, 21, 34, ... (ряд Фибоначчи) каж |
Паччоли |
называл |
золотое |
сечение |
|||||||||||||||||||
дый последующий член, начиная с |
"божественной |
пропорцией", |
а |
не |
|||||||||||||||||||
3-го равен сумме двух |
предыду |
мецкий ученый А.Цейзинг провозг |
|||||||||||||||||||||
щих. Отношение между смежными |
ласил |
золотое |
сечение |
универсаль |
|||||||||||||||||||
членами — такого ряда, начинал с |
ной |
пропорцией, |
|
равно |
характер |
||||||||||||||||||
5-го |
члена, |
практически постоянно |
ной |
для |
современных |
творений |
|||||||||||||||||
и |
равно |
1,62. |
|
|
|
|
|
|
|
|
природы и искусства. Золотое сече |
||||||||||||
|
Замечательным свойством |
ариф |
ние использовал в своем творчестве |
||||||||||||||||||||
метического, |
гармонического и |
гео |
И.В.Жолтовский, а Ле Корбюзье |
||||||||||||||||||||
метрического |
рядов |
является |
то, |
положил его в основу своего "Моду- |
|||||||||||||||||||
что каждое из чисел представляет |
лора". |
|
|
|
|
|
|
|
|
||||||||||||||
собой |
соответственно |
среднее |
ариф |
Золотое |
сечение |
|
выражают |
||||||||||||||||
метическое, |
среднее |
гармоническое |
обычно числом 1,618 или обратным |
||||||||||||||||||||
и |
среднее |
геометрическое |
предыду |
ему числом 0,618, для которых по |
|||||||||||||||||||
щего и последующего членов. Так, |
предложению |
Т.Куба |
и |
|
М.Бара |
||||||||||||||||||
в арифметической |
прогрессии |
1, 2, |
приняты символы Ф и 1/Ф. Эти |
||||||||||||||||||||
3 число 2 =(3+1)/2; в гармониче |
числа |
являются |
знаменателями. |
||||||||||||||||||||
ской |
прогрессии |
1/2, |
1/3, |
1/4 |
число |
возрастающего |
(Ф) |
и |
убывающего, |
||||||||||||||
1/3 = 2/(2+4); в геометрической |
(1/Ф) рядов золотого сечения. Ин |
||||||||||||||||||||||
прогрессии 1, 2, 4 число 2 = 1x4/2. |
тересной |
особенностью |
этих |
чисел |
|||||||||||||||||||
го, |
Поэтому |
числа |
арифметическо |
является их способность при сложе |
|||||||||||||||||||
гармонического |
и |
геометриче |
нии с единицей (для Ф) и при вы |
||||||||||||||||||||
ского |
рядов |
|
называют |
|
средними |
читании из единицы.(для 1/Ф) да |
|||||||||||||||||
числами. |
Средние |
|
числа |
издавна |
вать квадраты самих себя, т.е. |
1 + |
|||||||||||||||||
служили |
|
архитекторам, |
скульпто |
Ф + Ф 2 ; |
1 — |
1/Ф = (1/Ф)2 . Золотое |
|||||||||||||||||
рам и художникам в качестве сред |
сечение — это единственная геомет |
||||||||||||||||||||||
ства |
достижения |
гармоничных |
со |
рическая |
прогрессия, |
обладающая |
|||||||||||||||||
отношений. |
|
|
|
|
|
|
|
|
|
признаком аддитивного ряда (Ф 3 = |
|||||||||||||
|
Наиболее известным и в то же |
Ф1 + Ф2 ). |
|
|
|
|
|
|
|
||||||||||||||
время |
загадочным |
рядом |
средних |
Пропорционирование |
как |
метод |
|||||||||||||||||
чисел является так называемое от |
количественного |
согласования |
час |
||||||||||||||||||||
ношение |
золотого |
|
сечения. |
Термин |
тей и целого имеет в своей основе |
||||||||||||||||||
"золотое сечение" был введен Лео |
геометрическую |
или числовую |
за |
||||||||||||||||||||
нардо да Винчи для известного еще |
кономерность, |
которая |
способствует |
||||||||||||||||||||
пифагорейцам |
описанного |
Эвкли- |
достижению эстетической |
целостно |
|||||||||||||||||||
дом деления отрезка в так называе |
сти, гармоничности объемно-про |
||||||||||||||||||||||
мом "крайнем и среднем отноше |
странственной формы за счет объе |
||||||||||||||||||||||
нии", при котором большая его |
динения ее размеров в какую-либо |
||||||||||||||||||||||
часть |
является |
средней |
пропорцио |
систему. |
|
|
|
|
|
|
|
|
|||||||||||
76 Часть II. Средства архитектурной композиции
Особенности |
|
пропорциональных |
рце. 93. Деление от |
|
|
|
|
|
|||||||||||
|
: тесно связаны со способами |
резка АВ |
в крайнем |
равносторонних |
|
||||||||||||||
строительства |
и |
измерения, |
кото |
|
|
|
|
|
|
||||||||||
рые |
применялись |
архитекторами |
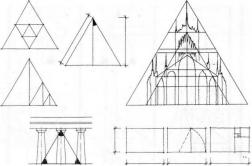
Рис. 94. |
"Священ- |
|
треугольников |
|
||||||||||||
той или иной эпохи. В древности |
|
Рис. |
97. |
Система |
|
||||||||||||||
пропорциональные системы |
получа |
треугольник и |
про- |
триангулирования |
|
||||||||||||||
ли с |
помощью |
мерного |
шнура |
и |
Миланского собора |
|
|||||||||||||
порционирование |
на |
|
|||||||||||||||||
кольев путем относительно простых |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
Рис. |
98. |
Система |
|
|||||||||||
геометрических |
построений |
на |
ос |
|
|
|
|
|
|
||||||||||
нове |
треугольника, |
квадрата, |
пря |
Рис. 95. |
Система |
|
триангулирования |
в |
|||||||||||
моугольника или круга. |
|
|
|
|
пропорционирования |
греческой |
архитек |
|
|||||||||||
В Древнем Египте широко ис |
|
|
|
|
|
туре |
|
|
|
|
|||||||||
пользовалась |
система пропорциони |
|
|
|
|
|
Рис. |
99. |
Построение |
||||||||||
рования на основе "священного еги |
Рис. |
96. |
Система |
|
ряда |
Золотого сече- |
|
||||||||||||
петского треугольника" с соотноше |
|
|
|
|
|
|
|||||||||||||
нием |
сторон |
3:4:5, |
позволявшего |
пропорционирования |
|
|
|
|
|
||||||||||
получать прямой угол и ряд прямо |
|
|
|
|
|
|
|
|
|
|
|||||||||
угольников со сторонами, |
выражен |
лее |
поздние |
времена, |
например, |
в |
|||||||||||||
ными |
в |
простых |
целых |
числах |
средневековье |
для |
построения готи |
||||||||||||
(рис. |
94). |
|
|
|
|
|
|
|
|
||||||||||
|
пропорционирования |
ческих |
башен; отношение |
стороны |
|||||||||||||||
Система |
и |
диагонали |
квадрата |
связывают |
|||||||||||||||
на основе вписанных квадратов да |
древнерусскую сажень и |
|
косую |
||||||||||||||||
вала геометрический ряд с отноше |
|
|
|
|
|
|
|
|
|
|
|||||||||
нием 1 :У2, в котором чередовались |
|
Система |
вписанных |
равносто |
|||||||||||||||
иррациональные |
и |
целые |
|
простые |
ронних треугольников дает ряд на |
||||||||||||||
числа (рис.95). Эта система исполь |
основе |
двух |
чередующихся |
отноше |
|||||||||||||||
зовалась |
как в |
Египте, так |
и в бо |
ний: стороны |
треугольника |
к высо- |
|||||||||||||
Глава 6. Пропорции |
77 |
те (2/ V 3) и высоты |
к половине сто |
рассекают |
его |
на треугольники |
|||||||||||||||
роны (г/3) (рис.96). Пропорциониро- |
именно с такими углами (рис. 100), |
||||||||||||||||||
вание |
на |
основе |
равностороннего |
ряд золотого сечения может быть |
|||||||||||||||
треугольника особенно широко при |
получен также на основе пентаг |
||||||||||||||||||
менялось в средневековье, где сис |
раммы — пятиугольной звезды, об |
||||||||||||||||||
тема триангулирования пронизыва |
разованной продлением сторон |
пра |
|||||||||||||||||
ла всю структуру готических собо |
вильного |
пятиугольника |
(рис. |
101) |
|||||||||||||||
ров |
|
(рис.97), |
однако |
отношения, |
или |
звездчатого |
десятиугольника |
||||||||||||
свойственные |
этой |
системе, |
могут |
(рис. 102). Ряд золотых отношений |
|||||||||||||||
быть обнаружены и в архитектуре |
неоднократно |
обнаруживались |
мно |
||||||||||||||||
других эпох, например, в архитек |
гочисленными |
|
исследователями в |
||||||||||||||||
туре Древней Греции (рис.98). |
|
памятниках |
архитектуры |
Египта, |
|||||||||||||||
|
Золотой |
прямоугольник |
может |
Греции, Рима, Русского и Западно- |
|||||||||||||||
быть |
получен |
построением |
квадрата |
Европейского |
средневековья, Ренес |
||||||||||||||
АВСД, как показано на рис.96,а,б. |
санса. |
|
|
|
|
|
|
|
|||||||||||
Если |
|
рассматривать |
квадрат |
как |
|
Перечисленные системы пропор- |
|||||||||||||
часть полученного |
прямоугольника, |
ционирования |
являются |
геометри |
|||||||||||||||
то |
|
стороны |
оставшегося |
|
прямо |
ческими, |
в |
числовом |
выражении |
||||||||||
угольника будут соотноситься в зо |
они менее удобны в использовании, |
||||||||||||||||||
лотом сечении. Этот процесс можно |
так |
как включают |
иррациональные |
||||||||||||||||
повторить, чтобы получить ряд зо |
числа. Однако |
существуют |
пропор |
||||||||||||||||
лотых |
прямоугольников |
(рис. 99). |
циональные |
системы, |
основанные |
||||||||||||||
В |
золотом |
отношении |
находят |
на |
числовых |
|
(арифметических) |
||||||||||||
ся |
стороны |
равнобедренных |
тре |
приемах согласования частей и це |
|||||||||||||||
угольников, с |
углами |
36°72° и |
72° |
лого; это так называемые модуль |
|||||||||||||||
или 108? 36"и 36е. Поскольку диаго |
ные |
системы. |
Простейшим |
приме |
|||||||||||||||
нали |
|
правильного |
пятиугольника |
ром |
модульной |
системы |
является |
||||||||||||
78 Часть II. Средства архитектурной композиции
масштабная сетка, в которую впи |
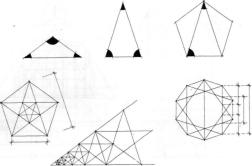
Рис. |
100. Золотое |
Рис. |
102. |
Система |
|||||||||
сываются как общий абрис, так и |
сечение и пятиу- |
|
пропорционирования |
|||||||||||
детали сооружения. Модульная сис |
|
|
|
на основе звездча |
||||||||||
тема |
пропорционирования |
предпо |
Рис. |
101. Система |
того |
десятиуголъ- |
||||||||
лагает |
существование модуля |
— ус |
|
|
|
|||||||||
пропорционирования |
|
|
|
|||||||||||
ловной |
единицы |
измерения. |
Мо |
Рис. |
103. |
Система |
||||||||
|
|
|
||||||||||||
дульные пропорции |
широко приме |
раммы |
|
модульных |
пропор |
|||||||||
нялись на протяжении всего разви |
|
|
|
ций в греческом ор- |
||||||||||
тия архитектуры. |
|
Наиболее |
ярким |
|
|
|
|
|
|
|||||
примером модульной системы |
про |
|
|
|
|
|
|
|||||||
порционирования |
является |
построе |
|
|
|
|
|
|
||||||
ние античных ордеров, в которых в |
|
|
|
|
|
|
||||||||
качестве |
модуля |
используется |
либо |
ния |
уже созданных архитектурных |
|||||||||
диаметр, |
либо |
радиус |
колонны |
форм. При этом следует понимать, |
||||||||||
(рис. 103). Применяемая в нашей |
что |
закономерности, выявленные в |
||||||||||||
стране |
модульная |
система |
(ЕМС) |
уже |
созданных |
архитектурных |
||||||||
так же использует единый модуль |
формах, далеко не всегда осознанно |
|||||||||||||
(М — 100 см), на основе которого |
применялись |
их |
создателями. Сле |
|||||||||||
путем его членения или умножения |
дует также помнить, что пропорци |
|||||||||||||
получают все принятые в строи |
онирование — |
достаточно |
сильное, |
|||||||||||
тельстве |
размеры. |
|
|
|
|
|
но далеко не единственное средство |
|||||||
Пропорционирование |
|
может |
гармонизации |
архитектурной фор |
||||||||||
быть использовано в двух основных |
мы и поэтому одно только совер |
|||||||||||||
направлениях: как |
метод |
создания |
шенство пропорции еще не являет |
|||||||||||
целостной формы и как метод вы |
ся гарантом получения совершенно |
|||||||||||||
явления |
закономерностей |
построе- |
го архитектурного произведения. |
|||||||||||
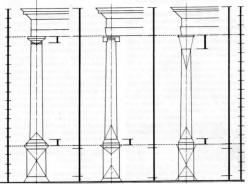
Глава 6. Пропорции |
79 |
Ко1ттрольные вопросы |
6. Какие системы пропорционирования |
|
вы знаете? |
||
1. Что такое пропорция? В каких значе |
7. |
В чем состоит отличие геометриче |
ниях может употребляться его понятие? |
ских и числовых систем пропорционирова |
|
2. Что такое непрерывная пропорция? |
ния ? |
|
3. Что такое "средние числа"? В чем |
8. |
Что такое модуль? |
причина преимущественного использования |
9. |
Назовите основные направления ис |
средних чисел для гармонизации форм? |
пользования пропорционирования в архитек- |
|
4. Что такое "золотое сечение"? В чем |
|
|
особенности этого отношения? |
10. Достаточно ли совершенных пропор |
|
5. В чем состоит разница между пропор |
ций для получения совершенного архитек |
|
цией и пропорционированием? |
турного произведения? |
|
80Часть П. Средства архитектурной композиции
ГЛАВА 7. МАСШТАБНОСТЬ
7.1.Понятие масштабности
вархитектуре. Человек как мера организуемого пространства. Близ кие По звучанию слова "масштаб" и "масштабность" в архитектуре име ют, однако, различные значения. Понятие "архитектурный масштаб" (в почти полном соответствии с об щим определением масштаба в сло варях1 ) включают прежде всего представления человека о величин
ном соотношении всего здания и его частей, частей или фрагментов здания и его деталей, здания или комплекса зданий и окружающего пространства — контекста, в кото ром существует здание или другой архитектурный объект. В соответст вии с этим можно считать, что не которая композиция (отдельный объем или комплекс объемов) имеет крупный масштаб в том случае, ес ли она состоит из достаточно круп ных в сравнении с ее общей вели чиной частей (или элементов). В то же время, композиция (любая ар хитектурная форма2 , расчлененная на более мелкие элементы, обладает мелким масштабом или менее крупным масштабом. Мы убедимся в этом, если построим из бумаги несколько композиций с различны ми масштабными характеристика ми, которые могут быть сопоставле ны в том случае, если рядом с каж дым примером поместить условное изображение фигуры человека од ной высоты.
1 Масштаб (нем. Ма51аЬ): 1. Отношение уменьшенных расстояний и размеров на кар те или чертеже к действительным. 2. Охват.значение, размах (по Толковому словарю русского языка под ред. Д.Н.Ушакова. М., ГИИ и Н2С, 1938).
2 Еше раз напоминаем, что понятие "ар хитектурная форма" относится не только к
ре и отражает представление о пространстве, организованном средствами архитектуры.
Однако представление об архи тектурном масштабе как результат количественного соотношения меж ду целым и его частями затрагива ет лишь один из аспектов важной проблемы масштабности архитек турной среды — количественно-гео метрический, связанный лишь с измерением, математическими дей ствиями, фиксирующими положе ние вещей. Значительно более важ ным моментом в постижении смыс ла и сути архитектурного масштаба является необходимость разобраться в том, почему те или иные -здания или пространства различаются по масштабным характеристикам. Для этого необходимо привлечь понятие масштабности как важной качест венной характеристики архитек турной среды, одной из централь ных категорий1 архитектурной композиции.
Мы называем архитектурное пространство масштабным в том случае, если человек, находящийся в нем (идущий по улице, пересека ющий площадь, двигающийся или просто находящийся в пространстве интерьера), ощущает это простран ство, воспринимает его и соответст венно оценивает как соразмерное, удобное, соответствующее назначе нию, постижимое и осваиваемое, т.е. "свое". Сложность, однако, за ключается в том, что когда мы го ворим "человек", следует всегда принимать во внимание, что "чело века вообще" не существует, что че ловек живет в определенном месте на Земле, в определенный истори ческий период и принадлежит к определенному социальному сооб ществу, к определенной культуре и, наконец, к определенной возра стной группе. Все эти обстоятельст-
1 Категория (греч. ка1еког,а) — предель но широкое понятие, в котором отражены наиболее общие существенные признаки,
