Вопрос 1: Различаются ли распределения предпочтений, выявлен­ные по каждому из четырех типов мужественности, между собой?

Для выявления различий между четырьмя распределениями лучше всего применить критерий χ². Критерий λ не применим по трем причи­нам: 1) n<50; 2) разряды представляют собой номинативную шкалу, так как при переходе от типа к типу изменяется "качество", а не "количество" мужественности; 3) критерий λ позволяет сопоставлять только 2 распределения одновременно, а в нашу задачу входит одно­временное сопоставление четырех распределений.

Сформулируем гипотезы.

H₀: Распределения предпочтений, выявленные по четырем типам муже­ственности, не различаются между собой.

H₁: Распределения предпочтений, выявленные по четырем типам муже­ственности, различаются между собой.

Рассчитаем теоретические частоты для каждой ячейки таблицы эмпирических частот (Табл. 9.18) по формуле:

f_{А теор} =31-31/124=7.75

f_{Б теор} =31-31/124=7,75 и т. д.

Поскольку суммы по всем строкам и столбцам таблицы равны, теоретические частоты для всех 16-ти ячеек таблицы будут одинаковы­ми. Равенство же по строкам и столбцам объясняется тем, что каждая испытуемая совершала принужденный выбор, так что каждый из типов мужественности был выбран 31 раз (даже если он был "выбран на последнее место).

Эта задача напоминает шутливый литературный пример, в кото­ром одна невеста совершала выбор из четырех женихов. В данном же случае у нас 31 испытуемая, и каждая совершает выбор из четырех ти­пов мужественности, распределяя их по четырем позициям.

Определим количество степеней свободы V для четырех типов мужественности (k) и четырех позиций выбора (с):

v=(k-l)-(c-l)=(4-l) (4-l)=3·3=9

Все дальнейшие расчеты произведем в таблице по Алгоритму 13 без поправки на непрерывность, так как при v>1 она не требуется.

Таблица 9.18

Расчет критерия χ² при сопоставлении распределений четырех типов мужественности по четырем позициям (n=31)

Разряды- типы мужественности	Позиции выбора	Эмпирическая частота fэ	Теоретическая частота fт	fэ- fт	(fэ- fт)2	(fэ- fт)2/ fт
1. Мифологически тип	1	2	7,75	-5,75	33,063	4,266
	2	6	7,75	-1,75	3,063	0,395
	3	4	7,75	-3,75	14,063	1,815
	4	19	7,75	+11,25	126,563	16,331
2. Национальный ТИП	1	19	7,75	+11,25	126,563	16,331
	2	4	7,75	-3,75	14,063	1,815
	3	7	7,75	-0,75	0,563	0,073
	4	1	7,75	-6,75	45,563	5,879
3, Современный ТИП	1	7	7,75	-0,75	0,563	0,073
	2	10	7,75	+2,25	5,063	0,653
	3	12	7,75	+4.25	18,063	2,331
	4	2	7,75	-5,75	33,063	4,266
4, Религиозный ТИП	1	3	7,75	-4,75	22,563	2,911
	2	11	7,75	+3,25	10,563	1,362
	3	8	7,75	+0,25	0,063	0,008
	4	9	7,75	+1,25	1,563	0,202
Суммы		124	124,0	0		58,711

По Табл. IX Приложения 1 определяем критические значения χ² при V=9:

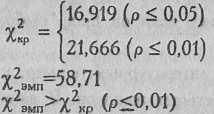
Ответ: H₀ отвергается. Принимается H₁. Распределения пред­почтений по четырем типам мужественности различаются между собой.