8.3. Двухфакторный дисперсионный анализ для связанных выборок

Назначение метода

Данный вариант двухфакторного дисперсионного анализа приме­няется в тех случаях, когда исследуется действие двух факторов на од-ну и ту же выборку испытуемых.

Описание метода

Допустим, мы измерили одни и те же показатели у одних и тех же испытуемых несколько раз - в разное время, в разных условиях, с помощью параллельных форм методики и т. п., и нам необходимо про­вести множественное сравнение показателей, изменяющихся при пере­ходе от условия к условию. Критерий L Пейджа для анализа тенденций изменения признака и критерий χ²_r Фридмана неприменимы, так как необходимо определить тенденцию изменения признака под влиянием двух факторов одновременно. Это позволяет сделать только дисперси­онный анализ.

Фактически в данной модели дисперсионного двухфакторного анализа проверяются 4 гипотезы: о влиянии фактора А, о влиянии фак­тора В, о влиянии взаимодействия факторов А и В и о влиянии факто­ра индивидуальных различий.

В данном варианте дисперсионного анализа нам потребуются две рабочие таблицы, которые позволят рассчитывать сумму по разным комбинациям ячеек комплекса. Рассмотрим это на примере, являющемся продолжением примера из п. 3.3.

Пример

В выборке курсантов военного училища (юноши в возрасте от 18 до 20 лет) измерялась способность к удержанию физического волевого усилия на динамометре. В первый день эксперимента у них, наряду с другими показателями, измерялась мышечная сила каждой из рук. На второй день эксперимента им предлагалось выдерживать на динамометре мышечное усилие, равное '/₂ максимальной мышечной силы данной руки. На третий день эксперимента испытуемым предлагалось проделать то же самое в парном соревновании на глазах у всей группы. Пары соревную­щихся были подобраны таким образом, чтобы сила обеих рук у них примерно совпадала. Результаты экспериментов представлены в Табл. 8.5. Можно ли считать, что фактор соревнования в группе каким-то обра­зом влияет на продолжительность удержания усилия? Подтверждается ли предположение о том, что правая рука более "социальна"?

Таблица 8.5

Длительность удержания усилия (сек/10) на динамометре правой и левой руками в разных условиях измерения (n=4)

Код имени испытуемого	Наедине с экспериментатором (A1)		В группе сокурсников (A2)
	Правая рука	Левая рука	Правая рука	Левая рука
1 Л-в 2 С-с 3 С-в 4 К-в	11	10	15	10
	13	11	14	10
	12	8	8	5
	9	10	7	8

Заметим, что единицы измерения в Табл. 8.5 - это секунды, но в каждом случае количество секунд уменьшено в 10 раз. Это законный способ преобразования индивидуальных значений, направленный на об­легчение расчетов. Для того, чтобы не оперировать трехзначными чис­лами, мы можем разделить их на какую-либо константную величину или уменьшить их на какую-либо константную величину (подробнее см п. 7.2).

Преобразуем таблицу индивидуальных значений в две рабочие таблицы двухфакторного дисперсионного комплекса для связанных вы­борок (Табл. 8.6 и 8.7). Мы видим, что здесь приведены суммы ин­дивидуальных значений отдельно по градациям фактора А (вне группы - в группе) и по градациям фактора В (правая рука - левая рука), по сочетаниям градаций А₁В_1, А₁В₂, А₂В_1, А₂В₂, а также суммы всех ин­дивидуальных значений каждого испытуемого и общие суммы.

Таблица 8.6 Двухфакторный дисперсионный комплекс по оценке влияния фактора А (вне группы - в группе) и фактора В (правая - левая рука) на дли­тельность удержания физического волевого усилия (сек/10) - вариант I

Код имени испытуемого	A1 - вне группы				А2 - в группе					Индивидуальные суммы всех 4-х значений
	B1	B2	Индивидуальные суммы по A1 (В1+В2)		B1		B2	Индивидуальные суммы по А2 (В1+В2)
1. Л-в 2. С-с 3. С-в 4. К-в	11 13 12 9	10 11 8 10	21 24 20 19		15 14 8 7		10 10 5 8	25 24 13 15		46 48 33 34
Суммы по ячейкам	45	39			44		33
Суммы по града­- циям At и А?				84					77
Общая сумма										161

Таблица 8.7

Двухфакторный дисперсионный комплекс по оценке влияния факторов А и В на длительность физического волевого усилия (сек/10) - вариант II

Код имени испытуемого	B1 – правая рука				B2 – левая рука					Индивидуальные суммы всех 4-х значений
	A1	A2	Индивидуальные суммы по B1 (A1+A2)		A1		A2	Индивидуальные суммы по B2 (A1+A2)
1. Л-в 2. С-с 3. С-в 4. К-в	11 13 12 9	15 14 8 7	26 27 20 16		10 11 8 10		10 10 5 8	20 21 13 18		46 48 33 34
Суммы по ячейкам	45	44			39		33
Суммы по града­- циям At и А?				89					72
Общая сумма										161

Мы видим, что в Табл. 8.7 фактически только две ячейки ком­плекса поменялись местами: A₁B₂ и A₂B₁. Это позволяет нам с боль­шей легкостью подсчитать суммы по градациям B₁ и В₂. Если бы 'мы пользовались только Табл. 8.6, то нам пришлось бы подсчитывать их "через столбец" и, кроме того, трудно было бы их куда-то подходящим образом записать. В дальнейшем при расчетах мы всякий раз будем указывать, к какой таблице лучше обратиться для извлечения нужных сумм, первой (I) или второй (II).

Установим некоторые величины, которые будут необходимы для расчёта критериев F.

Таблица 8.8

Величины, необходимые для расчета критериев F в двухфакторном дисперсионном анализе для связанных выборок

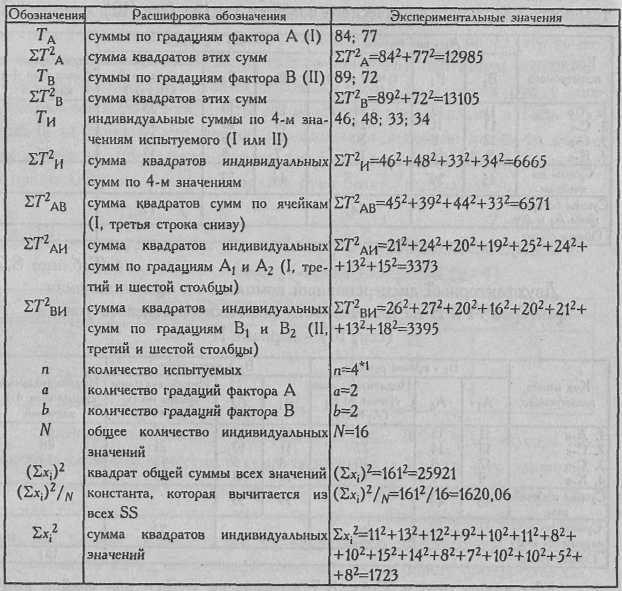
Теперь при расчетах будем лишь подставлять уже подсчитанные значения тех или иных величин. В случае, если какой-то из шагов в алгоритме расчетов будет не вполне ясен, можно вернуться к Табл. 8.8 и восстановить процедуры расчетов, или к Табл. 8.6 и Табл. 8.7, для того, чтобы вспомнить, почему мы подставляем в формулу ту или иную конкретную величину.

_____________

На самом деле в эксперименте участвовало 20 человек. В дисперсионный ком­плекс случайным образом отобраны 4 из них в целях упрощения расчетов. Резуль­таты дисперсионного анализа по такой "усеченной" выборке совпадают с данными обработки всей выборки с помощью критерия χ²_r.

Таблица 8.9

Последовательность операций в двухфакторном дисперсионном анализе для связанных выборок

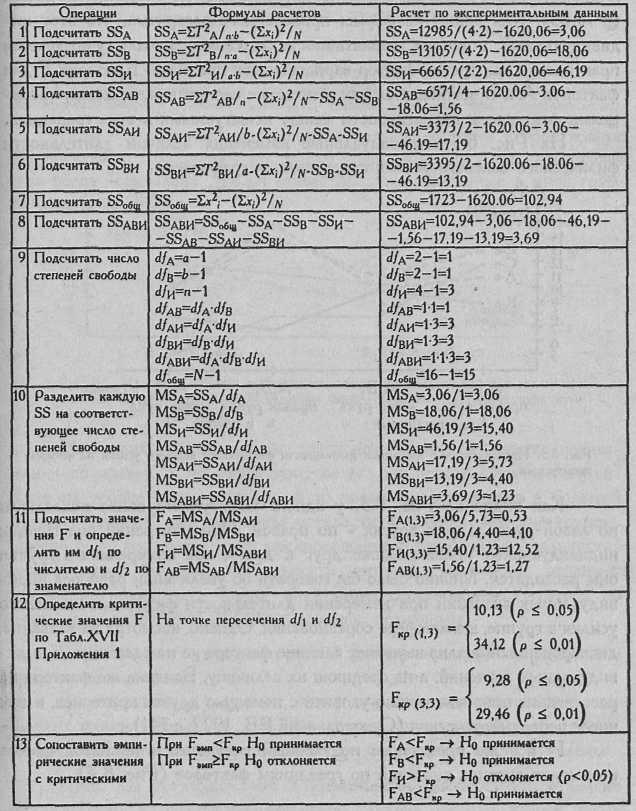
Мы видим, что влияние факторов А и В, как каждого в отдель­ности, так и в их взаимодействии, незначимо. В то же время фактор индивидуальных различий между испытуемыми (F_и) оказался значимым (р<0,05). Мы видим из формы приведенного алгоритма, что этот ин­дивидуальный источник вариативности с самого начала учитывается практически как третий фактор вариативности признака. Критерий F для факторов А и В вычисляется как отношение вариативности между града­циями факторов к вариативности между испытуемыми в этих градациях.

На Рис. 8.3 индивидуальные изменения величин длительности физического волевого усилия представлены графически.

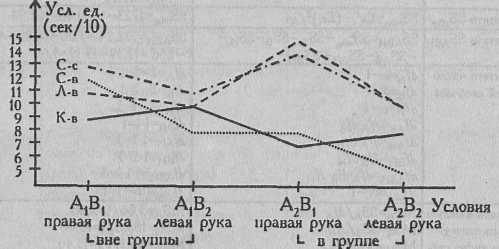
Рис. 8.3. Индивидуальные изменения длительности физического волевого усилия по четырем испытуемым

Как видно из Рис. 8.3, у одного испытуемого выше показатели по левой руке, у трех других - по правой. При измерении вне группы индивидуальные кривые ближе друг к другу, при измерениях в группе они расходятся. Можно было бы говорить об увеличении разброса инди­видуальных значений при измерении длительности физического волевого усилия в группе, в атмосфере соревнования. Однако, несмотря на название, дисперсионный анализ выявляет влияние фактора не на рассеивание инди­видуальных значений, а на среднюю их величину. Влияние же фактора на рассеивание признака можно уловить с помощью других критериев, в том числе непараметрических (Суходольский Г.В., 1972, с.341).

И все же представим полученный результат в принятой форме изменения средних значений по градациям факторов (Рис. 8.4).

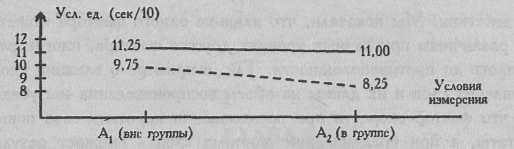
Рис. 8.4. Изменения средних величин длительности физического волевого усилия при переходе от индивидуальных замеров к групповым (правая рука - сплошная линия, левая рука - пунктирная линия)

Если исследователя интересует в большей степени второй вопрос данной задачи, связанный с проверкой предположения о том, что правая рука более "социальна", то он может представить данные в иной груп­пировке (Рис. 8.5).

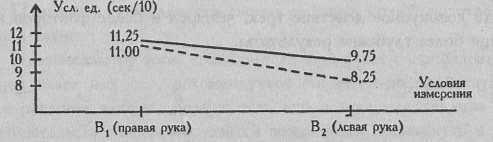
Рис. 8.5. Изменения средних величин длительности физического волевого усилия при переходе от правой руки к левой (сплошная линия - измерения вне группы, пунктирная линия - измерения в группе)

Мы видим, что во втором, групповом, замере снижаются показа­тели и по правой, и по левой руке, но все же правая рука "держится" почти на уровне первого замера, в то время как левая рука в большей степени "сдается" под влиянием усталости в группе, чем вне группы. Можно было бы подтвердить предположение о большей "социальности правой руки, большая стабильность которой, возможно, отражает стремление поддержать "лицо" в ситуации соревнования в группе, но выявленные тенденции, как мы убедились, незначимы.

Ограничения двухфакторного дисперсионного анализа для связанных выборок

Все ограничения такие же, как и в модели для несвязанных вы­борок, с одним уточнением. Все испытуемые должны пройти все сочета­ния градаций двух факторов. Этим достигается равномерность комплекса.

Итак, мы убедились, что двухфакторный дисперсионный анализ действительно позволяет нам оценить влияние двух факторов в их взаимодействии. Мы показали, что влияние одного фактора может ока­заться различным при разных уровнях другого фактора, иногда различ­ным вплоть до противоположности. Так, в примере о влиянии скорости предъявления слов и их длины на объем воспроизведения мы убедились в том, что фактор скорости при предъявлении коротких слов повышает результаты, а при предъявлении длинных слов - снижает результаты испытуемых.

Дисперсионный анализ позволяет также доказать, что влияние индивидуальных различий может оказаться сильнее экспериментальных или иных факторов, как это было продемонстрировано в последнем из примеров.

Более сложные схемы дисперсионного анализа позволяют ана­лизировать совокупное действие трех, четырех и более факторов и по­лучить еще более глубокие результаты.