9.3. Решения задач Главы 3
Решение задачи 4
Оценки отношения к наказаниям определены для 3-х условий, и вопрос задачи требует проверки достоверности тенденции в оценках. Целесообразнее всего было бы использовать критерий тенденций L Пейджа, но количество испытуемых п=16, а критические значения критерия L определены только для n≤12. Используем вначале критерий Фридмана, а затем все же попробуем использовать критерий L, разделив выборку на 2 части.
Решение задачи с использованием критерия χ2r Фридмана
Сформулируем гипотезы:
H0: Испытуемые примерно в одинаковой степени оправдывают (признают возможными) телесные наказания, которые их ребенок может получить от них самих, от бабушки и от воспитательницы (или учительницы).
H1: Испытуемые в разной степени оправдывают телесные наказания; которые их ребенок может получить от них самих, от бабушки и от воспитательницы (или учительницы).
Проранжируем оценки каждого испытуемого по трем условиям. Ранжирование производится по строкам, при этом меньшая оценка получает меньший ранг, большая оценка - наибольший ранг (Табл. 9.5).
Таблица 9.5
Оценки допустимости телесных наказаний со стороны разных людей и их ранги (n=16)
|
Испытуемые |
Условие 1: "Я сам" |
Условие 2: "Бабушка" |
Условие 3: "Учительница" | |||
|
Оценка |
Ранг |
Оценка |
Ранг |
Оценка |
Ранг | |
|
1 |
4 |
3 |
2 |
2 |
1 |
1 |
|
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
3 |
5 |
3 |
4 |
1.5 |
4 |
1.5 |
|
4 |
4 |
3 |
3 |
2 |
2 |
1 |
|
5 |
3 |
2.5 |
3 |
2.5 |
2 |
1 |
|
6 |
4 |
2 |
5 |
3 |
1 |
1 |
|
7 |
3 |
2.5 |
3 |
2.5 |
1 |
1 |
|
8 |
5 |
2,5 |
5 |
2.5 |
3 |
1 |
|
9 |
6 |
3 |
5 |
2 |
3 |
1 |
|
10 |
2 |
2 |
2 |
2 |
2 |
2 |
|
11 |
6 |
3 |
3 |
2 |
2 |
1 |
|
12 |
5 |
3 |
3 |
1 |
4 |
2 |
|
13 |
7 |
3 |
5 |
2 |
4 |
1 |
|
14 |
5 |
2,5 |
5 |
2,5 |
2 |
1 |
|
15 |
5 |
2,5 |
5 |
2,5 |
4 |
1 |
|
16 |
6 |
2.5 |
6 |
2.5 |
4 |
1 |
|
Суммы |
71 |
42 |
60 |
34,5 |
40 |
19,5 |
|
Средние |
4.44 |
3,75 |
2,50 | |||
Как видно из Табл. 9.5, суммы рангов по каждому условию составляют: 42; 34,5; 19,5, что в сумме равняется 96.
Расчетная сумма рангов:
Реально полученная и расчетная суммы совпадают, мы можем переходить к дальнейшим расчетам.
Определим эмпирическое значение χ2r :
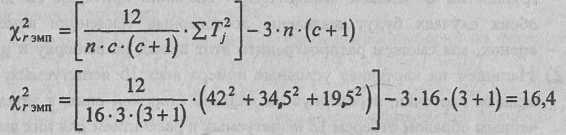
В нашем случае количество условий с=3, однако п>9, поэтому мы не можем воспользоваться таблицами, специально рассчитанными для критерия χ2r. Нам придется сопоставлять полученное эмпирическое значение с критическими значениями критерия χ2r. Число степеней свободы определяем по формуле:
v=c–1=3–1=2.
По Табл. IX Приложения 1 определяем критические значения для v=2:
Ответ: H0 отклоняется. Принимается H1. Испытуемые в разной степени оправдывают телесные наказания, которые их ребенок может получить от них самих, от бабушки и от воспитательницы (учительницы).
Решение с использованием критерия тенденций L Пейджа
Из Табл. 9.5 видно, что испытуемые, похоже, склонны более снисходительно относиться к тем наказаниям, которые они сами дают детям (T1=42), несколько менее снисходительно они относятся к бабушкиным наказаниям (T2=34,5), и еще менее снисходительно - к наказаниям со стороны воспитательницы или учительницы, хотя бы и "за дело (T3=19,5). Метод Пейджа требует, чтобы мы расположили условия в порядке возрастания ранговых сумм: условия 1, 2 и 3 становятся, соответственно, условиями 3, 2 и 1, как показано в Табл. 9.6.
Имеющиеся таблицы критических значений критерия L рассчитаны только для небольших выборок (n≤12). В исследованной выборке n=16. Попробуем обойти это ограничение следующими двумя способами:
1) Разделим выборку пополам и рассчитаем отдельно для каждой подгруппы из 8 человек эмпирическое значение критерия L. Если в обоих случаях будут выявлены достоверные тенденции изменения оценок, мы сможем распространить этот вывод на выборку в целом.
2) Напишем на карточках условные номера всех 16 испытуемых, перемешаем карточки, перевернув их лицевой стороной вниз, а затем случайным образом отберем 12 испытуемых и рассчитаем для них эмпирическое значение критерия L. Этот метод применяется в дисперсионном анализе для уравновешивания комплексов (см. Главы 7 и 8).
Мы можем применить в данном случае и сам дисперсионный анализ, но ограничимся пока этими двумя способами.
Таблица 9.6
Оценки допустимости телесных наказаний и их ранги в упорядоченной для критерия L последовательности (n1=8; n2=8)
|
Испытуемые |
Условие 1 (бывшее 3): "Учительница" |
Условие 2 (бывшее 2): "Бабушка" |
Условие 3 (бывшее 1): "Я сам" | |||
|
Оценка |
Ранг |
Оценка |
Ранг |
Оценка |
Ранг | |
|
1 |
1 |
1 |
2 |
2 |
4 |
3 |
|
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
3 |
4 |
1,5 |
4 |
1,5 |
5 |
3 |
|
4 |
2 |
1 |
3 |
2 |
4 |
3 |
|
5 |
2 |
1 |
3 |
2,5 |
3 |
2,5 |
|
6 |
1 |
1 |
5 |
3 |
4 |
2 |
|
7 |
1 |
1 |
3 |
2,5 |
3 |
2,5 |
|
8 |
3 |
1 |
5 |
2,5 |
5 |
2,5 |
|
Суммы |
15 |
9,5 |
26 |
18 |
29 |
20,5 |
|
Средние |
1,875 |
3,25 |
3,63 | |||
|
9 |
3 |
1 |
5 |
2 |
6 |
3 |
|
10 |
2 |
2 |
2 |
2 |
2 |
2 |
|
И |
2 |
1 |
3 |
2 |
6 |
3 |
|
12 |
4 |
2 |
3 |
1 |
5 |
3 |
|
13 |
4 |
1 |
5 |
2 |
7 |
3 |
|
14 |
2 |
1 |
5 |
2,5 |
5 |
2,5 |
|
15 |
4 |
1 |
5 |
2,5 |
5 |
2,5 |
|
16 |
4 |
1 |
6 |
2,5 |
6 |
2,5 |
|
Суммы |
25 |
10 |
34 |
16,5 |
42 |
21,5 |
|
Средние |
3,125 |
4,25 |
5,25 | |||
Сформулируем гипотезы.
H0: Повышение оценок допустимости телесных наказаний от первого условия к третьему случайно.
H1: Повышение оценок допустимости телесных наказаний от первого условия к третьему не случайно.
Определим L1 и L2 для двух половин нашей выборки по формуле:
L1=∑(Tj·j)=(9,5·1)+(18·2)+(20,5·3)=9,5+36+61,5=107 L2=∑(Tj·j)=(10·1)+(16,5·2)+(21,5·3)=10+33+64,5=107,5
По Табл. VIII Приложения 1 определяем критические значения L для п=8, с=3:
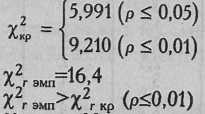
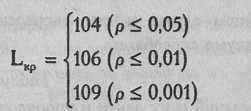
Построим "ось значимости"
Мы видим, что для обеих половин выборки Lэмп>Lкр, что позволяет нам отвергнуть нулевую гипотезу (р≤0,01).
Теперь используем второй способ сокращения выборки.
Случайным образом отобраны 12 испытуемых из 16: 1, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 16. Все расчеты для этой усеченной выборки представлены в Табл. 9.7.
Таблица 9.7
Расчет критерия L по оценкам допустимости телесных наказаний для усеченной выборки испытуемых (п=12)
|
Испытуемые |
Условие 1: "Учительница" |
Условие 2: "Бабушка" |
Условие 3: "Я сам" | ||||
|
Оценка |
Ранг |
Оценка |
Ранг |
Оценка |
Ранг | ||
|
1 |
№1 |
1 |
1 |
2 |
2 |
4 |
3 |
|
2 |
№3 |
4 |
1,5 |
4 |
1.5 |
5 |
3 |
|
3 |
№4 |
2 |
1 |
3 |
2 |
4 |
3 |
|
4 |
№5 |
2 |
1 |
3 |
2,5 |
3 |
2,5 |
|
5 |
№6 |
1 |
1 |
5 |
3 |
4 |
2 |
|
6 |
№7 |
1 |
1 |
3 |
2,5 |
3 |
2,5 |
|
7 |
№8 |
3 |
1 |
5 |
2,5 |
5 |
2,5 |
|
8 |
№9 |
3 |
1 |
5 |
2 |
6 |
3 |
|
9 |
№10 |
2 |
2 |
2 |
2 |
2 |
2 |
|
10 |
№12 |
4 |
2 |
3 |
1 |
5 |
3 |
|
11 |
№14 |
2 |
1 |
5 |
2,5 |
5 |
2,5 |
|
12 |
№16 |
4 |
1 |
6 |
2,5 |
6 |
2,5 |
|
Суммы |
29 |
14,5 |
46 |
26 |
52 |
31,5 | |
|
Средние |
2,42 |
|
3,83 |
|
4,33 |
| |
Lэмп=(14,5·1)+(26·2)+(31,5·3)=14,5+52+94,5=161
По Табл. VIII Приложения 1 определяем критические значения L для n=12, с=3:
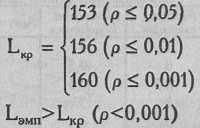
Ответ: Hq отклоняется. Принимается H1. Повышение оценок от первого условия к третьему неслучайно (р<0,001). Испытуемые менее всего склонны соглашаться на то, чтобы воспитательница или учительница применяла телесное наказание по отношению к их ребенку, более склонны соглашаться с тем, чтобы это делала бабушка и еще более склонны позволять это делать себе.
Но, конечно, когда мы говорим о меньшей или большей склонности, то ориентируемся на эмпирически установленный диапазон значений и средние величины, которые "на глаз" не так уж сильно различаются и составляют, соответственно: 2,50; 3,75; 4,44 по 7-балльной шкале.
Решение задачи 5