8.2. Двухфакторный дисперсионный анализ для несвязан­ных выборок

Назначение метода

Данный вариант двухфакторного дисперсионного анализа приме­няется в тех случаях, когда исследуется одновременное действие двух факторов на разные выборки испытуемых, т. е. когда разные выборки, испытуемых оказываются под воздействием разных сочетаний двух факторов. Количество выборок определяется количеством ячеек диспер­сионного комплекса.

Описание метода

Суть метода остается прежней, но в двухфакторном дисперсион­ном анализе мы можем проверить большее количество гипотез. Расчеты гораздо сложнее, чем в однофакторных комплексах.

Используемый в данном руководстве алгоритм расчетов предна­значен только для равномерных комплексов. Если комплекс получился неравномерным, необходимо случайным образом отсеять несколько ис­пытуемых.

Работу начинаем с построения специальной таблицы, отражаю­щей весь дисперсионный комплекс. Подробности лучше сразу рассмат­ривать на примере.

Пример

Рассмотрим пример из руководства J.Greene, M.D.'Olivera (1989).

Четырем группам испытуемых предъявлялись списки из 10 слов:

группе 1 - короткие слова с большой скоростью;

группе 2 - короткие слова с медленной скоростью;

группе 3 - длинные слова с большой скоростью;

группе 4 - длинные слова с медленной скоростью.

В каждой группе было по 4 испытуемых, всего N=16. Предска­зывалось, что между факторами длины слов и скоростью их предъявле­ния будет наблюдаться значимое взаимодействие: при большой скоро­сти предъявления лучше будут запоминаться короткие слова, а при медленной скорости - длинные слова. Результаты экспериментов пред­ставлены в Табл. 8.1.

Таблица 8.1

Количество воспроизведенных слов при разной длине слов и разной скорости их предъявления (по J.Greene, M.D'Olivera, 1989)

Переменная (фактор) В скорость предъявления слов	Переменная (фактор) А - длина слов				Суммы по пере­менной В (ТB)
	A1 - короткие слова		A2 - длинные слова
В1 (большая скорость)	9867	30	5334	15	45
B2 (малая скорость)	4335	15	7567	25	40
Суммы по переменной А (ТA)		45		40	85

Заметим, что в отечественных руководствах чаще предлагается другая, более привычная для нас, форма таблиц для двухфакторных дисперсионных комплексов (Табл. 8.2). При такой форме легче "увидеть" комплекс в целом.

Таблица 8.2

Двухфакторный дисперсионный комплекс по оценке влияния фактора А (длина слов) и фактора В (скорость предъявления слов) на количество воспроизведенных слов

Градации фактора А	А1 - короткие слова		A2 – длинные слова
Градации фактора В	B1	B2	B1	B2
	9 8 6 7	4 3 3 5	5 3 3 4	7 5 6 7
Суммы по ячейкам	30	15	15	25
Суммы по градациям фактора А	ТA1=45		ТA2=40.
Суммы по градациям фактора В	ТB1==30+15=45		ТB2==15+25=40

Как видим, при такой форме таблицы легче подсчитать суммы по ячейкам (в столбик), но труднее разобраться с суммами по градациям каждого из факторов. В данном случае оказалось, что они совпали:

Т_A1= Т_B1; Т_A2= Т_B2.

В дальнейшем при использовании алгоритма расчетов будем опи­раться на Табл. 8.1.

Сформулируем гипотезы. Это будут гипотезы, касающиеся влия­ния фактора А отдельно от фактора В (как бы при "усредненных" его значениях), гипотезы о влиянии фактора В отдельно от фактора А и гипотезы о влиянии взаимодействия градаций факторов А и В.

1 комплект гипотез

H₀: Различия в объеме воспроизведения слов, обусловленные действием фактора А, являются не более выраженными, чем случайные раз­личия между показателями.

H₁: Различия в объеме воспроизведения слов, обусловленные действием фактора А, являются более выраженными, чем случайные различия между показателями.

2 комплект гипотез

H₀: Различия в объеме воспроизведения слов, обусловленные действием фактора В, являются не более выраженными, чем случайные раз­личия между показателями.

H₁: Различия в объеме воспроизведения слов, обусловленные действием фактора В, являются более выраженными, чем случайные различия между показателями.

3 комплект гипотез

H₀: Влияние фактора А на объем воспроизведения слов одинаково при разных градациях фактора В, и наоборот.

H_1: Влияние фактора А на объем воспроизведения слов различно при разных градациях фактора В, и наоборот.

Используя экспериментальные значения, представленные в Табл. 8.1, установим некоторые величины, которые будут необходимы для расчета критериев F.

Таблица 8.3

Величины, необходимые для расчета критериев F в двухфакторном дис­персионном анализе для несвязанных выборок

Напомним, что при подсчете ∑ x _i² все индивидуальные значения сначала возводятся в квадрат, а потом суммируются, а при подсчете (∑ x _i)² все индивидуальные значения сначала суммируются, а затем их общая сумма возводится в квадрат.

Последовательность расчетов представлена в Табл. 8.4.

Таблица 8.4

Последовательность операций в двухфакторном дисперсионном анализе для несвязанных выборок

Вывод: Но принимается в комплектах гипотез 1 и 2. Различия в объеме воспроизведения слов, обусловленные в отдель­ности факторами А и В, не являются более выраженными, чем слу­чайные различия между показателями. H₀ отвергается для взаимо­действия факторов (3 комплект). Принимается H₁. Влияние фактора А на объем воспроизведения слов различно при разных градациях фактора В, и наоборот (р≤0,01).

Итак, оказывается, что факторы длины слов и скорости их предъявления в отдельности не оказывают значимого действия на объем воспроизведения. Значимым оказывается именно взаимодействие фак­торов: короткие слова лучше запоминаются при быстрой скорости предъявления, а длинные - при медленной скорости предъявления (см. Рис. 8.2). Таким образом, предположение, высказанное авторами, на­шло статистически значимое подтверждение (р≤0,001).

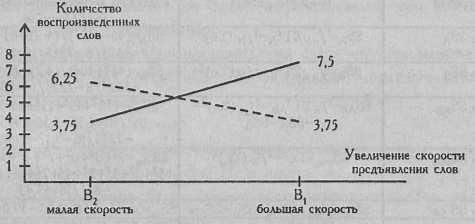
Рис. 8.2. Кривые изменения объема воспроизведения при повышении скорости предъ­явления коротких (сплошная линия) и длинных слов (пунктирная линия)

Ограничения двухфакторного дисперсионного анализа для несвязанных выборок

1. У каждого фактора должно быть не менее двух градаций.

2. В каждой ячейке комплекса должно быть не менее двух наблюдае­мых значений для выявления взаимодействия градаций.

3. Количества значений во всех ячейках комплекса должны быть равны для обеспечения равенства дисперсий в ячейках комплекса и для ис­пользования приведенного выше алгоритма расчетов; для неравно­мерных комплексов можно использовать алгоритмы Н.А. Плохинского (1970).

4. Комплекс должен представлять собой симметричную систему: каж­дой градации фактора А должно соответствовать одинаковое количе­ство градаций фактора В.

5. Результативный признак должен быть нормально распределен в ис­следуемой выборке, в противном случае значимые различия будет выявить гораздо труднее и применение метода будет не вполне кор­ректным.

6. Факторы должны быть независимыми. В рассмотренном примере скорость предъявления слов и их длина - внешне независимые фак­торы. В других случаях независимость факторов может быть под­тверждена отсутствием корреляционной связи между переменными, выступающими в качестве факторов.