9.4. Решения задач Главы 4

Решение задачи 6

Вопрос 1: Можно ли утверждать, что разные картины методики Хекхаузена обладают разной побудительной силой в отношении моти­вов: а) "надежда на успех"; б) "боязнь неудачи"?

Для того, чтобы ответить на этот вопрос, необходимо сопоставить распределение реакций "надежда на успех" и реакций "боязнь неудачи" с равномерным распределением. Тем самым мы проверим, равномерно ли распределяются реакции "надежды на успех" по шести картинам и равно­мерно ли распределяются реакции "боязни неудачи" по шести картинам.

Количество наблюдений достаточно велико, чтобы мы могли ис­пользовать любой из классических критериев - χ² или λ. Однако, как мы помним, картины в данном исследовании предъявлялись разным испытуемым в разных последовательностях, следовательно, мы не мо­жем говорить об однонаправленном изменении признака в какую-либо одну сторону: все разряды (картины) следуют друг за другом в слу­чайном порядке. Это является веским основанием для применения кри­терия χ² и отказа от критерия λ.

Рассмотрим оба аспекта поставленного вопроса последовательно.

А) Равномерно ли распределяются реакции "надежды на успех" по шести картинам методики Хекхаузена?

H₀: Распределение реакций "надежды на успех" не отличается от рав­номерного распределения.

H₁: Распределение реакций "надежды на успех" отличается от равно­мерного распределения.

Рассчитаем теоретические частоты для равномерного распределе­ния по формуле:

где n - количество наблюдений,

k - количество разрядов.

В данном случае количество наблюдений - это количество реак­ций "надежды на успех" у 113 испытуемых. Таких реакций зарегистри­ровано 580, следовательно, n =580. Количество разрядов - это количе­ство стимульных картин, следовательно, k=6. Определяем f_теор:

Количество степеней свободы V определяем по формуле:

v= k -l=6-l=5

Итак, поправка на непрерывность не нужна, мы можем произво­дить все расчеты по общему алгоритму. Они представлены в Табл.9.11.

Таблица 9.11

Расчет критерия χ² при сопоставлении распределения реакций "надежды на успех" по 6 картинам с равномерным распределением

Разряды-картины методики		Эмпирические частоты реакций "надежды на успех" fэ	Теоретические частоты реакции "надежды на успех" fт	fэ- fт	(fэ- fт)2	(fэ- fт)2/ fт
1 2 3 4 5 6	"Мастер изме­ряет деталь" "Преподаватель и ученик" "В цехе у машины" "У двери ди­ректора" "Человек в бюро" "Улыбающийся юноша"	106 102 108 50 99 115	96,67 96,67 96,67 96,67 96,67 96,67	9,33 5,33 11,33 -46,67 2,33 18,33	87,05 28,41 128,37 2178,09 5,43 335,99	0,90 0,29 1,33 22,53 0,06 3,48
Суммы		580		0		28,59

По Табл. IX Приложения 1 определяем критические значения χ² для v=5:

Построим "ось значимости".

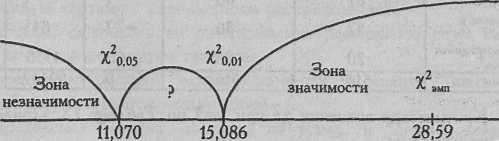
χ²_эмп = 28,59

χ²_эмп > χ²_кр

Ответ: H₀ отклоняется. Принимается H₁. Распределение реак­ций "надежды на успех" по шести картинам методики Хекхаузена от­личается от равномерного распределения (р<0,01).

Б) Равномерно ли распределяются реакции "боязни неудачи" по шести картинам методики Хекхаузена?

H₀: Распределение реакций "боязни неудачи" не отличается от равно­мерного распределения.

H₁: Распределение реакций "боязни неудачи" отличается от равномер­ного распределения.

В данном случае количество наблюдений - это число реакций "боязни неудачи", следовательно, n=516; количество разрядов - это число стимульных картин, как и в предыдущем случае, следовательно, k=6. Определяем f_теор

f_теор =⁵¹⁶/₆=86

Количество степеней свободы v=k—1=6—1=5. Поправка на не­прерывность здесь тоже, естественно, не нужна.

Все дальнейшие расчеты проделаем по алгоритму в таблице.

Таблица 9.12

Расчет критерия при сопоставлении распределения реакций "боязни неудачи" по 6 картинам с равномерным распределением

Разряды-картины методики		Эмпирические частоты реакций "боязни неудачи" fэ	Теоретические частоты реакции "боязни неудачи" fт	fэ- fт	(fэ- fт)2	(fэ- fт)2/ fт
1 2 3 4 5 6	"Мастер изме­ряет деталь" "Преподаватель и ученик" "В цехе у машины" "У двери ди­ректора" "Человек в бюро" "Улыбающийся юноша"	138 180 34 87 57 20	86 86 86 86 86 86	52 94 -52 1 -29 -66	2704 8836 2704 1 841 4356	31,44 102.74 31,44 0.01 9.78 50,65
Суммы		516	516	0	19442	226,06

Критические значения χ² при v=5 по Таблице IX Приложения 1 нам уже известны:

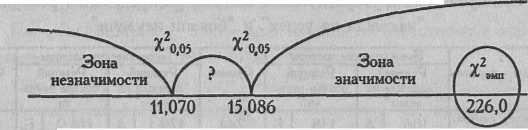
χ²_эмп > χ²_кр

Ответ: H₀ отклоняется. Принимается H₁. Распределение прояв­лений "боязни неудачи" по шести стимульным картинам отличается от равномерного распределения (р<0,01).

Итак, реакции "надежды на успех" и реакции "боязни неудачи" неравномерно проявляются в ответ на 6 стимульных картин. Однако это еще не означает, что эти картины являются неуравновешенными по направленности воздействия. Может оказаться так, по крайней мере теоретически, что одни и те же картины вызывают большинство реакций обоих типов, а другие картины почти не вызывают реакций или вызывают их достоверно меньше. В этом случае оба эмпирических распределения отличались бы от равномерного, но не различались бы между собой.

Проверим, различаются ли картины теперь уже не по количеству вы­зываемых реакций, а по их качеству, то есть вызывают ли одни картины скорее реакции "надежды на успех", а другие - реакции "боязни неудачи"