Вопрос 2: Можно ли считать стимульный набор методики Хекхаузена неуравновешенным по направленности воздействия?

Решим эту задачу двумя способами: а) путем сравнения распре­деления реакций "надежда на успех" с распределением реакций "боязнь неудачи" по 6-и картинам; б) путем сопоставления распределения реак­ций на каждую картину с равномерным распределением.

Выясним, совпадают ли распределения реакций по двум карти­нам. Для этого сформулируем гипотезы.

H₀: Распределения реакций "надежда на успех" и реакций "боязнь не­удачи" не различаются между собой.

H₁: Распределения реакций "надежда на успех" и "боязнь неудачи" различаются между собой.

Для того, чтобы облегчить себе задачу подсчета теоретических частот, воспроизведем таблицу эмпирических частот и дополним ее.

Таблица 9.13

Эмпирические и теоретические частоты распределения реакций "надежда на успех" и "боязни неудачи"

Разряды - картины		Эмпирические частоты				Суммы	Теоретические частоты				Суммы
		Реакций "надежда на успех"		Реакций "боязнь неуда­чи"			Реакций "надежда на успех"		Реакций "боязнь неуда­чи"
1 2 3 4 5 6	"Мастер измеря­ет деталь" "Преподаватель и ученик" "В цехе у маши- "У двери дирек­тора" "Человек в бюро" "Улыбающийся юноша"	106 102 108 50 99 115	А В д ж и л	138 180 34 87 57 20	Б Г Е 3 К M	244 282 142 137 156 135	129,1 149,2 75,1 72,5 82,6 71,4	А В Д Ж И Л	114,9 132,8 66,9 64,5 73,4 63,6	Б Г Е 3 К М	244 282 142 137 156 135
Суммы		580		516		1096	580		516		1096

Расчет теоретических частот осуществляется по известной нам формуле:

Произведем расчеты.

f_{А теор}=244·580/1096=129,1

f_{Б теор}=244·516/1096=114,9

f_{В теор}=282·580/1096=149,2

f_{Г теор}=282·516/1096=132,8

f_{Д теор}=142·580/1096=75,1

f_{Е теор}=142·516/1096=66,9

f_{Ж теор}=137·580/1096=72,5

f_{З теор}=137·516/1096=64,5

f_{И теор}=156·580/1096=82,6

f_{К теор}=156·516/1096=73,4

f_{Л теор}=135·580/1096=71,4

f_{М теор}=135·516/1096=63,6

По Табл. 9.13 мы видим, что сумма всех теоретических частот равна общему количеству наблюдений, а попарные суммы теоретических частот по строкам равны суммам наблюдений по строкам.

Расчеты критерия χ² будем производить по известному алгоритму. Поправка на непрерывность не вносится, так как v>1:

v=(r-l)(c-l)=(6-l)(2-l)=5

Результаты всех операций по Алгоритму 13 представлены в Табл. 9.14.

Таблица 9.14

Расчет критерия χ² при сопоставлении эмпирических распределений реакций "надежды на успех" (НУ) и "боязни неудачи" (БН)

Ячейки таблицы частот		Эмпирическая частота fэ	Теоретическая частота fт	fэ- fт	(fэ- fт)2	(fэ- fт)2/ fт
1	А	106	129,1	-23,1	533,61	4,13
2	Б	138	114,9	23,1	533,61	4,64
3	В	102	149,2	-47,2	2227,84	14,93
4	Г	180	132,8	47,2	2227,84	16,78
5	Д	108	75,1	32,9	1082,41	14,41
6	Е	34	66,9	-32,9	1082,41	16,18
7	Ж	50	72,5	-22,5	506,25	6,98
8	3	87	64,5	22,5	506,25	7,85
9	И	99	82,6	16,4	268,96	3,26
10	К	57	73,4	-16,4	268,96	3,66
11	Л	115	71,4	43,6	1900,96	26,62
12	М	20	63,6	-43,6	1900,96	29,89
Суммы ,		1096	1096	0		149,33

Критические значения χ² при v=5 нам уже известны:

Построим "ось значимости".

χ²_эмп > χ²_кр

Ответ: H₀ отвергается. Принимается H₁. Распределения реакций "надежды на успех" и "боязни неудачи" различаются между собой.

Теперь выясним, совпадают ли распределения реакций по каждой картине. Сформулируем гипотезы.

H₀: Реакции двух видов в ответ на картину №1 (№2, №3 ... №6) распределяются равномерно.

H₁: Реакции двух видов в ответ на картину №1 (№2, №3 ... №6) распределяются неравномерно.

Реакции "надежды на успех" будем обозначать как НУ, реакции "боязни неудачи" - как БН.

Подсчитаем теоретические частоты для каждой из шести картин, по формуле:

где n общее количество реакций обоих направлений на данную картину; k - количество разрядов, в данном случае количество видов реакции (k =2).

f_{1 теор} =244/2=121;

f_{2 теор} =282/2=141;

f_{3 теор} =142/2=71;

f_{4 теор} =137/2=68,5

f_{5 теор} =156/2=78

f_{6 теор} =135/2=67,5

В данном случае число степеней свободы v=l:

v=k—1=2—1=1.

Следовательно, мы должны сделать во всех шести случаях по­правку на непрерывность. Проведем расчеты отдельно для каждой кар­тины (см. Табл. 9.15).

Таблица 9.15

Расчет критерия χ² при сопоставлении распределений реакций на каж­дую из шести картин с равномерным распределением

Определим по Табл. IX Приложения 1 критические значения для v=l:

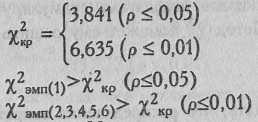
Ответ: H₀ отклоняется для всех картин. H₁ принимается для картин 2, 3, 4, 5 и 6: реакции двух видов в ответ на эти картины рас­пределяются неравномерно.

Если представить данные графически (Рис. 9.2), то легко можно видеть, что картины №6, №3 и №5 вызывают достоверно больше реакций "надежды на успех", а картины №2, №1 и №4 - достоверно больше реакций "боязни неудачи".

Стимульный набор методики Х. Хекхаузена оказался неуравнове­шенным по направленности стимулирующего воздействия.

Рис. 9.2. Соотношения частот реакций "надежда на успех" (незаштрнхованные столбн-ки) н реакций "боязнь неудачи" (заштрихованные столбики) по разным картинам мето­дики Х.Хекхаузена

Вместе с тем, из Рис. 9.2 мы можем заметить, что если частоты реакций "боязни неудачи" достаточно монотонно возрастают при пере­ходе от картины №6 к картине №3, а затем к №5, №4, №1 и №2, то частоты реакций "надежда на успех" по всем картинам, за исключе­нием картины №4, оказываются примерно на одном уровне, в диапазо­не от 99 до 115. Каждый исследователь сам для себя решает вопрос о том, что для него важнее - абсолютные показатели стимулирующего воздействия или их соотношения. Метод у} поможет ему решить зада­чи и первого, и второго типа.

Решение задачи 7