
Калин Физическое материаловедение Том 5 2008
.pdfтурой ГЦК равно 12. На свободной поверхности число связей атома может изменяться от минимальных трех до максимальных девяти, но не до двенадцати. Поскольку каждая связь понижает внутреннюю энергию атома на Ub/2 (Ub – энергия связи двух атомов), то энергия атома, расположенного на поверхности, вследствие порванных связей больше энергии в объеме. Таким образом, с поверхностью связан определенный избыток свободной энергии, зависящий от строения этой поверхности и носящий название по-
верхностной энергии или поверхностного натяжения.
Поверхностная энергия. Поверхностная энергия имеет опре-
деленное значение, соответствующее термодинамическому равновесию данной поверхности со своим насыщенным паром. При этом количество атомов, испаряющихся с поверхности, и атомов, конденсирующихся на поверхности в единицу времени, должно быть одинаковым.
Поверхностная энергия грани кристалла определяется расположением атомов, образующих эту грань, которое неодинаково для граней с различными индексами, т.е. с различной плотностью упаковки атомов на поверхности. Поэтому поверхностная энергия обладает определенной анизотропией. Полная поверхностная энергия кристалла определяется суммой поверхностных энергий всех его граней. Для описания анизотропии поверхностной энергии, т.е. зависимости поверхностной энергии от ориентации поверхности, используют специальные трехмерные диаграммы в полярных координатах, так называемые -диаграммы, с которыми можно познакомиться в специальной литературе. Поверхностная энергия, как и многие физические свойства металлов, является периодической функцией порядкового номера в Периодической системе элементов Д.И. Менделеева, причем чередование максимальных и минимальных значений этой величины совпадает с чередованием таких свойств, как плотность и сжимаемость. В целом, с увеличением порядкового номера возрастает и поверхностная энергия.
Поверхностная энергия измеряется в Дж/м2 и, по-видимому, связана с рядом физических свойств атомов. Например, известно уравнение, дающее удовлетворительную связь поверхностной энергии с работой выхода электронов на определенной плоскости (hkl):
351
(hkl) = k (hkl) (V / )5/6, |
(19.53) |
где V – число валентных электронов; – атомный |
объем; |
k = 1,15·103 для координационного числа атомов Z = 8 и k = 1,08·103
для Z = 12.
Определенное согласие вычисленных и экспериментальных значений поверхностной энергии установлено при использовании связи поверхностной энергии с теплотой сублимации металлов.
Поверхностная энергия расплавленного металла обычно увеличивается на треть при затвердевании, что позволяет использовать расплавы для оценки поверхностной энергии твердых сплавов. Связь между поверхностной энергией твердого и жидкого металла
можно определить и по формуле: |
|
тв = ж (dтв/dж)2/3 (Lтв / Lж), |
(19.54) |
где dтв и dж – плотность кристалла и расплава; Lтв и Lж – теплоты сублимации и испарения соответственно.
Поверхностная энергия и свободная поверхностная энергия связаны между собой через площадь поверхности dA следующим оче-
видным соотношением: |
|
Gпов = dA. |
(19.55) |
Наряду со свободными, существуют внутренние поверхности раздела, включая границы зерен, фаз, внутренние несовершенства (границы двойников) и дефекты (упаковки), обладающие соответствующей энергией. Внутренние поверхности разделяют по уровню энергии смещения атомов из занимаемого положения. Например, некогерентные двойниковые границы и границы зерен с большим углом разориентации обладают достаточно высоким уровнем поверхностной энергии. Когерентные двойниковые границы и дефекты упаковки обладают меньшим уровнем энергии.
Границы между зернами представляют собой слой смещенных атомов шириной порядка 2–3 межатомных расстояния. Условно принято считать, что энергия границы зерна В равна половине энергии свободной поверхности, т.е. В = а , где а = 0,5. На самом деле у металлов коэффициент а может быть отличным от 0,5, например: у алюминия а = 0,55; золота а = 0,29; меди а = 0,30; железа и вольфрама а = 0,38.
Поверхностное натяжение. Анализ поведения жидкостей (расплавов) показал, что поверхность ведет себя так, словно она по-
352
крыта стягивающим поверхностным слоем. Для описания этого «стягивания» введено понятие поверхностного натяжения, измеряемого в единицах Н/м. Поверхностное натяжение расплавов уменьшается с ростом температуры, выше температуры плавления Тпл, по закону:
= пл – d /dT (T – Tпл), |
(19.56) |
где пл – поверхностное натяжение при температуре плавления сплава.
Поверхностное натяжение и поверхностная энергия – понятия идентичные. В табл. 19.2 рассмотрены термодинамические оценки поверхностного натяжения и поверхностной энергии.
Полагая, что при увеличении площади поверхности поверхностная энергия остается постоянной из сравнения выражений (А) и (Б), представленных в табл. 19.2, получаем, что н э. Строго говоря, между поверхностным натяжением и поверхностной энерги-
ей существует следующая связь: |
|
|
|
|
н = э + А э / А. |
(19.57) |
|
|
|
Таблица 19.2 |
|
Термодинамическая оценка поверхностного натяжения |
|
||
|
и поверхностной энергии |
|
|
|
|
||
Поверхностное натяжение, Н/м |
Поверхностная энергия, Дж/м2 |
||
|
|
||
Под действием напряжения н по- |
Свободная энергия Гиббса связана с |
||
верхность необратимо |
увеличивает |
внутренней энергией следующим |
|
свою площадь на некоторую малую |
соотношением: |
|
|
величину dA, изменяя форму образца |
G = U + pV – TS. |
|
|
при постоянных значениях объема, |
С учетом постоянства давления, объ- |
||
температуры и давления. При этом |
ема и температуры для металлов |
||
выполняется работа W = н dA. |
можно записать |
|
|
По первому закону термодинамики |
dG = dU – T dS |
|
|
изменение внутренней энергии: |
или для внутренней энергии: |
|
|
dU = W + Q, |
|
dU = dG + T dS. |
|
а по второму закону Q = T dS. |
С учетом (19.55) связи свободной |
||
Для внутренней энергии получим |
поверхностной энергии с поверхност- |
||
следующую зависимость от поверх- |
ной энергией получим: |
|
|
ностного натяжения: |
|
dU = э dA + T dS. |
(Б) |
dU = н dA + TdS. |
(А) |
|
|
353
Из выражения (19.56) следует, что если при растяжении поверхности диффузионный поток атомов из объема обеспечивает постоянную плотность атомов на поверхности, то производная э / А
будет равна 0 и будет соблюдаться численное равенство н = э.
19.6.2. Процессы, контролируемые изменением поверхностной энергии
Избыточная свободная поверхностная энергия стимулирует протекание ряда процессов, идущих при Gпов min. ПриGпов = dA изменения могут быть связаны или с изменением уровня поверхностной энергии min, или с сокращением площади поверхности А min. Кроме этого, будем помнить, что избыток свободной поверхностной энергии определяет избыток химического потенциала :
= ( G / С)T , V , |
(19.58) |
значение которого при равновесии системы = 0.
Образование граней на кристаллах. При наличии шерохова-
тости поверхности общая поверхностная энергия будет складываться из множества слагаемых, соответствующих участкам поверхности. При нагревании такой поверхности с течением времени сохраняются плоскости с наиболее плотной упаковкой атомов как обладающие минимальными площадями поверхности и, следовательно, поверхностной энергии. В этом случае происходит огранение кристалла с сохранением наиболее плотноупакованных плоскостей (плоскостей с малыми индексами типа 111 ).
Элементарными физическими механизмами огранения кристаллов являются диффузия и сублимация (испарение) атомов. В результате, если кристалл мал, то образуется многогранник, а с ростом времени дальнейшее сокращение площади поверхности может привести к образованию сферы, обладающей минимальной площадью поверхности из известных геометрических фигур.
Рост частиц второй фазы. Мелкодисперсные выделения (частицы) второй фазы широко используются для упрочнения сплавов, при этом важно создать высокую плотность частиц и обеспечить её существование в условиях эксплуатации. Дисперсные частицы об-
354
ладают высоким суммарным уровнем поверхностной энергии межфазных границ и в совокупности дают высокий избыток свободной поверхностной энергии. При нагревании такая система будет стремиться сократить площадь поверхности, например, за счет растворения мелких и укрупнения крупных частиц, так как при этом наиболее эффективно сокращается площадь поверхностей межфазных границ. Такой процесс известен как рост частиц по ме-
ханизму Оствальда – коалесценция по Оствальду.
Удельная свободная энергия поверхности раздела металлических выделений и металлической матрицы обычно имеет значения от 0,02 Дж/м2 (например, когерентные выделения Ni3Al в никеле) до 0,6 Дж/м2 (для границ зерен). В случае некогерентных частиц оксида, например Th2O в никеле, удельная свободная энергия поверхности раздела может иметь значения до 1,5 Дж/м2.
Зная размер фазы и ее плотность, можно определить избыток энергии сплава. Например, в системе Cu–Co имеются когерентные выделения на расстоянии = 30 нм друг от друга. При этом их плотность 1022 м–3, а площадь поверхности А = 107 м2/м3. Если0,2 Дж/м2, то получим суммарное значение свободной поверхностной энергии G = 2 МДж/м3. Можно показать, что чем мельче фаза, тем больше общая площадь поверхности. Из отношения площади (А = 4 r2) к объему (V = 4/3 r3) частиц (при постоянном объеме) следует, что А = 3V/r. Видно, что чем меньше радиус, тем больше поверхность и, следовательно, больше G = dA. Отсюда следует довольно очевидный вывод о том, что малые частицы должны сильнее растворяться больших частиц из-за большей движущей силы.
Физический процесс укрупнения микроструктуры и высвобождение избыточной поверхностной энергии обусловлен более высокой растворимостью мелких частиц, имеющих большое отношение площади их поверхности к объему. Увеличение растворимости можно показать с помощью обычной фазовой диаграммы состояния системы и графика в координатах «энергия – состав сплава», представленных на рис. 19.18.
В случае мелкодисперсных -выделений радиусом r в - матрице равновесные растворимости С ( ) и С ( ) заменяются на С (r) и С (r). Состав твердого раствора на рис. 19.18, б представлен
355
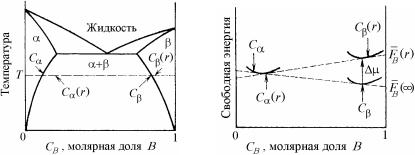
в молярных долях. Изменение равновесной растворимости вызвано увеличением химического потенциала (19.58) выделившейся фазы. Точки FB(r) и FB( ) на рис.19.18, б являются точками пересечения общих касательных с осью В (чистого компонента).
а |
б |
Рис. 19.18. Типичная фазовая диаграмма (а) и график зависимости свободной энергии Гельмгольца F(r) от состава (б): линия С –С соответствует равновесию плоских (r = ) выделений -фазы; линия С (r)–С (r) соответствует равновесию выделений -фазы конечного размера r
При переходе малого количества фазы (dn молей) состава С из выделения с плоской границей раздела (r = ) к выделению радиусом r имеет место прирост химического потенциала . Такой переход вызывает увеличение свободной энергии
dG = dF = dn = dA,
где А – площадь поверхности выделения, а считают изотропной. Следовательно, = dA/dn. Известно, что А = 4 r2, поэтому dA/dr = 8 r. Число молей выделений n в сфере радиуса r равно n = 4 r3/(3Vм), поэтому dn/dr = 4 r2/Vм, где Vм – молярный объем выделений, т.е. объем, занимаемый 6,02 1023 атомами. Тогда получаем dA/dn = 2Vм/r и окончательно
= 2 Vм/r. |
(19.59) |
Множитель 2/r представляет собой кривизну поверхности, которая для несферических поверхностей равна (1/ r1 + 1/r2), где r1 и r2 – два перпендикулярных радиуса кривизны несферической поверхности. Таким образом, при переходе плоского выделения в выделение с определенной кривизной (r) увеличивается свободная энергия
356
на , изменяя парциальную молярную свободную энергию (FB) и растворимость компонента В в -фазе, С (r).
Из уравнения (19.59) видно, что чем меньше радиус частицы второй фазы, тем выше уровень свободной энергии и больше дви-
жущая сила растворения такого выделения.
Используя уравнение (19.59), известные термодинамические уравнения для растворов и рис. 19.18, можно вывести уравнение
Гиббса–Томпсона: |
|
ln[C (r) / C ( )] = 2 Vм /RTr, |
(19.60) |
характеризующее состояние уровня растворимости компонента В в фазах. Для любых выделений радиусом в несколько нанометров существует следующее соотношение растворимости компонента В в -фазе:
С (r) = C ( ) (1 + 2 Vм /RTr), |
(19.61) |
где C ( ) – растворимость В в -фазе при плоском выделении. Следует подчеркнуть, что учет анизотропии поверхностной
энергии существенно усложняет вид уравнений и поэтому здесь не приводится.
При растворении мелких выделений и одновременном росте крупых выделений происходит процесс укрупнения выделений в целом (коалесценция).
В процессе роста частиц второй фазы их равновесная форма зависит не только от уровня поверхностной энергии, но и упругих напряжений, возникающих в процессе роста. В качестве примера часто рассматривают несферические равновесные формы. Такой равновесной формой могут быть стержни с закругленными торцами, как это показано на рис. 19.19, что обусловлено уровнем возникающих при росте упругих напряжений в решетке.
Минимум упругих напряжений возможен в случае кристаллографического совпадения плоскостей выделения и матрицы, например, ось медного выделения параллельна направлению плотной упаковки <110> ГЦК-атомов и <111> в ОЦК-матрице железа, т.е. Cu<110>(ГЦК)|| -Fe<111>(ОЦК). Отношение диаметр/длина стерженьковых выделений равно 1/4, что указывает на низкие значениядля поверхностей, в которых лежит направление плотной упаковки. Итак, в системе Cu–Fe равновесной формой выделений является стержень с отношением d/l = 1/4.
357

0,5 мкм
Рис. 19.19. Стерженьковые выделения меди в матрице железа, полученные при отжиге сплава Fe – 4 мас.% Cu в течение 300 ч при 953 К. Частицы, ось которых перпендикулярна плоскости фольги, имеют круглые сечения,
ачастицы, параллельные поверхности фольги, выглядят как стержни
сзакругленными концами
Вдругих системах равновесной формой выделений могут быть диски с отношением d/h = 25/1 (Al–Cu) или сферические выделения (Cu–Co). В большинстве работ по изучению роста выделений обнаружено, что в течение всего времени роста форма выделений остается неизменной, что свидетельствует о равновесности формы выделений.
Еще раз подчеркнем, что стабильная форма растущих частиц определяется соотношением поверхностной и упругой энергий в решетке системы. Это означает, что кинетика роста частиц второй фазы под действием избытка свободной поверхностной энергии весьма чувствительна к структуре среды, в которой идет рост. Повидимому, при разных условиях будут действовать различные механизмы роста в зависимости от места расположения частицы в твердом теле. Рассмотрим ряд ситуаций, определяющих рост частиц.
Рост выделений, контролируемый объемной диффузией.
Рост выделений происходит в объеме зерна твердого тела. На рис. 19.20 представлена простейшая система из двух сферических выделений, радиусы которых равны r1 и r2. Для этого случая наиболее подходящим механизмом роста -выделения является объемная диффузия атомов компонента В в -матрице.
358
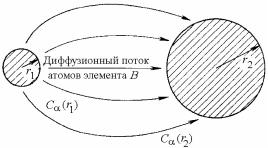
Рис. 19.20. Схематическое изображение двух сферических -выделений радиусами r1 и r2 в -матрице
В этом случае концентрация растворенного в матрице вещества возле каждого выделения будет соответствовать его равновесной растворимости. Но это означает, что количество растворенного вещества, находящегося в равновесии с выделением 1 – С (r1), будет больше, чем с выделением 2 – С (r2), так как поверхность выделения 1 меньше выделения 2. Поэтому возникнет диффузионный поток атомов В в направлении от 1 к 2, как это показано на рис. 19.20. По мере того, как r1 будет уменьшаться, а С (r1) – возрастать, процесс будет развиваться с возрастающей скоростью до тех пор, пока не произойдет исчезновения малого выделения и система не останется с относительно большим выделением.
Диффузионный поток (моль/с) к растущему выделению на
расстоянии R от него равен –4 R2D( С1 / R ). Здесь: С1 – концентрация, равная числу атомов в единице объема, т.е. молярная концентрация С, деленная на молярный объем Vм: С1 = С/Vм. В таком случае поток атомов:
= –4 R2D ( С / R )1/Vм. |
(19.62) |
Именно этот поток обусловливает скорость роста выделения
r/ t . Если учесть, что 1/r D С ( ) – С (r) , где C ( ) – равновесная концентрация твердого раствора с выделением среднего
размера rc, принять объем выделения V = (4/3) r3 и число молей внутри выделения n = V/Vм = 4 r3/3Vм, то после интегрирования и
преобразований получим для скорости роста уравнение |
|
r/ t = 2D VмC ( ) (1/rc–1/r)/RTr. |
(19.63) |
359 |
|
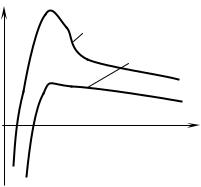
Зависимость (19.63) показана на рис. 19.21, из которой следуют следующие выводы:
1)все частицы радиусом меньше rс растворяются, а скорость растворения возрастает по мере уменьшения размера частицы;
2)все частицы, радиус которых больше rс, растут, а скорость роста увеличивается от 0 (при r = rс) до максимальной величины (при r = 2rc) и затем снижается;
3)по мере увеличения rс скорость роста всех выделений уменьшается.
Изменение среднего размера частиц со временем можно получить, если принять, что это изменение равно максимальному значению dr/dt при r = 2rc:
r 3 |
r 3 |
a |
Dσ VмCα t |
, |
(19.64) |
t |
0 |
1 |
RT |
|
|
|
|
|
|
||
где а1 = 8/9–3/2 для точного расчета; R – универсальная газовая постоянная.
Таким образом, при росте частиц второй фазы, контролируемом объемной диффузией атомов, радиус частицы во времени изменяется как
|
|
r t1/3. |
|
dr/dt |
r |
1 |
|
|
с |
|
|
|
|
r 2 |
Рис. 19.21. Изменение |
|
|
скорости контролируемого |
|
|
|
с |
|
|
|
|
диффузионного роста |
|
|
|
выделений dr/dt |
|
|
|
в зависимости от их радиуса |
|
|
|
для двух различных значений |
|
|
r |
среднего радиуса rc. |
|
|
Значение r 2 (для нижней |
|
с
кривой) больше, чем для верхней rс1
Рост выделений, контролируемый переносом атомов через межфазную границу. По своему строению межфазные границы (рис. 19.22) могут иметь различное строение: большеугловые, когерентные и полукогерентные. В случае большеугловых границ ато-
360
