Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

706 a. j. c. varandas and z. r. xu

GP effect, with the shifts being equal to þ0:0807, 0:0709, and 0:0273 eV for the A1, A2, and E symmetries, respectively. Clearly, such shifts are larger than those obtained in the calculations for the lower adiabatic potential energy surface, namely, þ0:0104, 0:0194, and 0:0043 eV (in the above order).

Similar to the case without consideration of the GP effect, the nuclear probability densities of A1 and A2 symmetries have threefold symmetry, while each component of E symmetry has twofold symmetry with respect to the line defined by b ¼ 0. However, the nuclear probability density for the lowest E state has a higher symmetry, being cylindrical with an empty core. This is easyly understand since there is no potential barrier for pseudorotation in the upper sheet. Thus, the nuclear wave function can move freely all the way around the conical intersection. Note that the nuclear probability density vanishes at the conical intersection in the single-surface calculations as first noted by Mead [76] and generally proved by Varandas and Xu [77]. The nuclear probability density of the lowest state of A1 (A2) locates at regions where the lower sheet of the potential energy surface has A2 (A1) symmetry in S3. Note also that the A1 levels are raised up, and the A2 levels lowered down, while the order of the E levels has been altered by consideration of the GP effect. Such behavior is similar to that encountered for the ‘‘trough states’’ [11].

The five lowest levels of A1 and A2 symmetries are found to keep the same order irrespectively of having or not considered the GP effect; by ascending

the GP effect is found to alter the order of the levels ð0; 1 Þ and ð2; 0 Þ with E symmetry. The fundamental frequencies for the symmetric stretching mode (A1 symmetry in the D3h point group) are 352.79, 352.87, and 353:83 cm 1 for A1, A2, and E symmetries in the S3 permutational group, respectively. In turn, the fundamental frequencies for the degenerate bending mode (E symmetry in the D3h point group) are 702.44, 748.50, and 769:94 cm 1 for A1, A2, and E symmetries in S3, respectively. Thus, no significant changes are observed in the fundamental frequencies of the symmetric stretching modes due to consideration of the GP effect, which implies similar shifts for the two involved eigenenergies. Note that due to the GP effect, the electronic wave function changes sign when traversing a path that encircles the conical intersection. However, the nuclear wave function now has a corresponding change of sign to compensate that in the electronic wave function. The lowest level in the complete spectrum with consideration of the GP effect is then of E symmetry in the S3 permutation group. As seen, there are considerable differences in the E vibronic wave functions due to inclusion of the GP effect. This can be attributed to having imposed the proper boundary conditions into the wave function and the fact that the E states involve a pseudorotation along the j coordinate.

We now address the fact that the symmetry of the vibrational modes must be adapted to the nuclear spin multiplicity. Since 7Li is a fermion with nuclear spin

to calculate the vibrational frequencies, which may be justified due to no specification of 7Li3 in [78]. Yet, test calculations have shown that the vibrational levels should not change by >1 or 2 cm 1 when 7Li3 is instead considered. In summary, to resolve the remaining discrepancy one requires to refine the potential energy surface and take full consideration of nonadiabatic effects.

As for the trough states, a statistical analysis has been carried out for the calculated cone states [12]. The nearest neighbor spacings are calculated by

where E is the unfolded energy. In turn, the mean level spacing is given by

Xn

i ¼ 1

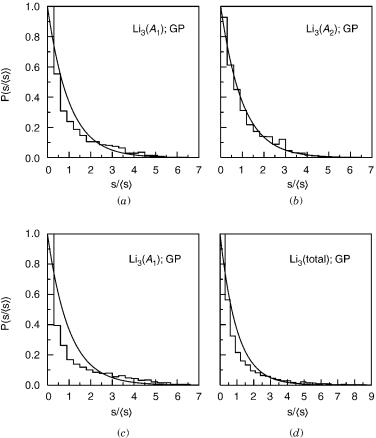
From these first and second moments, one can calculate the quantity hs2i=hsi2. The results so obtained [12] are given in Table XVI, while Figure 10 shows the corresponding neighbor spacing distributions. It is seen that the level distributions Pðs=hsiÞ take values in the interval 0 < Pð0Þ < 1 for all spectra, which implies in the strict sense of their definitions that they do not obey Wigner, Poisson, or Brody distributions. All spectra seem near Brody type in each block, while the full spectra look like near Poisson type. For each symmetry block, the spectra turn out to be more irregular than the full spectra, irrespectively of taking or not the GP effect into consideration. This is due to the strong interations among states with the same symmetry. However, there is no interation between states with different symmetry, and hence the spectra for each symmetry block are nearly irregular. In turn, the random superposition of unrelated sequences of energy levels leads the full spectra to be more regular.

TABLE XVI

Calculated hs2i=hsi2 for the Vibrational Levels of the First-Excited

Electronic Doublet State of Li3

710 a. j. c. varandas and z. r. xu

variation of the level spacings that decrease with energy, and (2) the accidental degeneracies and near degeneracies. If such degeneracies can be removed, the uniformity of a spectrum will increase. By this 2 standard, it is found that the spectra (full and those of each symmetry block) are more nonuniform for the cone states than for the trough states. To explain such a finding, one should note the significant differences between the lower and upper adiabatic sheets of the Li3 potential energy surface, in particular the fact that there is no barrier for pseudorotation on the upper adiabatic sheet. Thus, the pseudorotational motion in the upper sheet is faster than in the lower sheet, which implies a frequency o2 for pseudorotation of the degenerate mode considerably larger than that of the breathing mode (o1). For example, from our results for the A1 symmetric vibrational states with consideration of the GP effect, one has o2 ¼ 702 cm 1, which is nearly twice the value of the frequency o1 ¼ 353 cm 1 for the symmetric stretching mode. Thus, a lot of levels are expected to gather together leading to frequent accidental degeneracies or near degeneracies. Since in many cases the symmetry requirement for the occurence of Fermi resonances is absent, such degeneracies and near degeneracies cannot be removed. As a result, the first moment hsi will be small, and hence S2 becomes large and leads to an increase in nonuniformity of each symmetry block. Consider, for example, the ideal case where o2 ¼ 2o1. Obviously, the states ð2m þ n; kl2 Þ and ½n; ðm þ kÞl02 & are degenerate in the harmonic oscillator approximation since the energy does not depend on the value of the vibrational angular momentum quantum number. Then, it can be demonstrated by induction that the level ð2m þ n; kl2 Þ is ½intðk=2Þ þ int½ðk þ mÞ=2& þ 2&-fold degenerate in the above approximation (this will lead to a near degeneracy in the anharmonic approximation); ðn; kÞ are integers or zero, and m is a nonzero integer. If the above levels have the same symmetry, a Fermi resonance will occur; otherwise, it will be absent. For example, if m is odd there can be no Fermi resonance since the vibrational angular momentum quantum numbers are different. Specifically, for m ¼ 1, the ð2 þ n; 00Þ and ðn; 11Þ levels will not suffer a Fermi resonance, with the same being true for the degenerate levels ð2 þ n; 11Þ, ðn; 22Þ, and ðn; 20Þ. Instead, for m even, there will be 2½intðk=2Þ þ 1&, which will be subject to Fermi resonances. As a specific case, consider m ¼ 2: the levels ð4 þ n; 00Þ and ðn; 20Þ will suffer a Fermi resonance, while it will be absent for the ð4 þ n; 00Þ and ðn; 22Þ levels. In the case of m arbitrary but even, the number of levels that cannot be subject to Fermi resonances is given by ½int½ðk þ mÞ=2& intðk=2Þ&. Clearly, this number increases with increasing m. In summary, at least more than one-half of the degeneracies cannot be removed through Fermi resonances. As a result, the levels will be nonuniformly distributed, leading to an increased nonuniformity of the spectra.

To summarize, the dynamical Jahn–Teller effect is found to be more significant (about one order of magnitute larger) than the GP effect as far as the

vibrational states of Li3 are concerned. Regarding nonadiabatic coupling effects, a comparison of the Li3 calculations with the only available experimental datum suggests that they play a minor role (at most 0:004 eV, i.e., one order of magnitute smaller than that of the GP effect). Moreover, from the neighbor spacing distributions of the vibrational levels, it has been found that the spectra are quasiregular in short range and quasiirregular in long range, while the 2 standard indicates that the spectra are more nonuniform for the cone states than for the trough ones.

D.Nonadiabatic Coupling Effects

Nonadiabatic coupling between adiabatic (BO) potential energy surfaces leads to a breakdown of the BO approximation. The proper treatment then requires a coupled multistate calculation, which would lead to the exact vibronic levels. For X3-type systems such as Li3, we have two adiabatic potential energy surfaces that intersect originating an upper sheet with the shape of an inverted cone, and a lower sheet that looks like a trough. If one carries out a single surface generalized BO calculation (i.e., only with consideration of the GP effect), one obtains either the cone or trough states. For Li3, the cone states are bound states, although we must distinguish two types of cone states depending on whether they have energies higher than the dissociation energy of the lower surface or not. If they lie above the dissociation threshold, they are imbedded in a continuum and would show up as resonances in reactive scattering or longlived complexes in studies of unimolecular decomposition. As a result, these states (which are pseudobound states in the single surface calculation) are trully resonance states. If the energies of the cone states are not above the dissociation limit of the lower surface, they are imbedded in the discrete spectrum of the trough states. In this case, they are genuine bound states, and will interact strongly with any other states of the same symmetry. The levels associated to those states, as well as of states that are near the intersection seam, will further shift if nonadiabatic coupling is fully taken into account on the treatment of the problem. A quantitative assessment of such shifts would require the knowledge of the observed frequencies or rigorous nonadiabatic calculations carried out on the same potential energy surface. Unfortunately, such comparisons cannot be done at present.

E.Effects of Electron Spin and Nuclear Spin

For molecules with an even number of electrons, the spin function has only single-valued representations just as the spatial wave function. For these molecules, any degenerate spin–orbit state is unstable in the symmetric conformation since there is always a nontotally symmetric normal coordinate along which the potential energy depends linearly. For example, for an 3E state of a C3v molecule, the spin function has species esA2 and esE that upon

712 a. j. c. varandas and z. r. xu

multiplication by the species eoE of the orbital wave function leads to total

slightly unstable since in an orbitally nondegenerate state the spin–orbit coupling is always very small [28].

The situation is different for an electronic system with an odd number of electrons. By Kramers’ theorem, the vibronic coupling cannot remove the degeneracy caused by the half-integer spin S. Moreover, as Jahn [79] has shown, the antisymmetric product of the species of the spin–orbit wave function with itself must have the same species as one of the nontotally symmetric normal vibrations in order to make the Jahn–Teller instability possible. For all axial point groups, the antisymmetric product of any doubly degenerate two-valued representation with itself is totally symmetric; that is, E1=2; E3=2; . . . states cannot be split by vibronic coupling. Therefore, for all axial point groups when spin–orbit interaction is strong, there is no Jahn–Teller instability. Only a magnetic field such as that connected with a rotation can remove the degeneracy. As follows from the previous discussion, for an 2E state, the orbital part of the degeneracy will lead to a Jahn–Teller instability if the spin–orbit coupling is weak. For a strong spin–orbit interaction, 2E will split into two states eoE ! esE1=2 ¼ eE1=2 eE3=2, with each doublet component remaining doubly degenerate for arbitrary displacements of the nuclei. The general conclusion is that spin–orbit coupling for half-integer spin reduces the instability caused by orbital degeneracy. The above discussion can be applied to the nuclear spin if we consider the nucleus-spin electron–orbit coupling. However, since this coupling is generally smaller than the electron spin–orbit coupling, it may be necessary to take it into account only in special cases, for example, for large values of J.

F.Other Alkali Metal Trimers

In this section, we extend the above discussion to the isotopomers of X3 systems, where X stands for an alkali metal atom. For the lowest two electronic states, the permutational properties of the electronic wave functions are similar to those of Li3. Their potential energy surfaces show that the barriers for pseudorotation are very low [80], and we must regard the concerned particles as identical. The 23Na atom has a nuclear spin 32; 39K, 40K, and 41K have nuclear spins 32, 4, and 32; 85Rb and 87Rb have nuclear spins 52 and 32; and 133Cs has a nuclear spin 72. From the above discussion, it then follows that the permutation properties of molecules having individual half-integer spin nuclei will be similar

to those involving 7Li; conversely, the permutational properties of molecules consisting of integer spin nuclei will be similar to those containing 6Li.

G.1H3 and Its Isotopomers

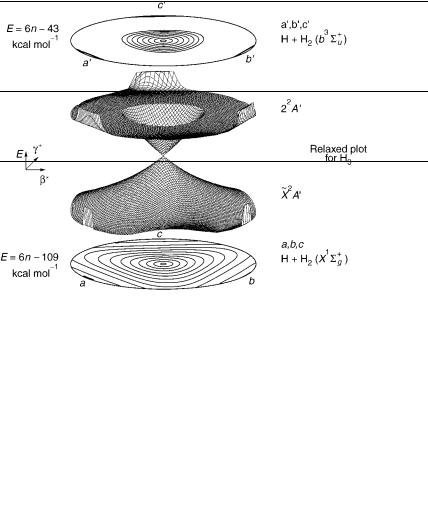
Now, briefly we discuss the molecule 1H3 and its isotopomers, while also highlighting their differences with respect to 7Li3. For the title systems, there have been many investigations, for example, [2,4,5,7,8,59,81], and references cited therein. Similarly to the lithium trimer, H3 and its isotopomers are important Jahn–Teller systems where the vE0 normal coordinates cause instability and lead to the splitting of the potential energy in the form of a conical intersection between the two involved adiabatic potential energy

~2 0 2 0

surfaces (X A and 2 A ). Note that intersections of similar kind may occur [81] involving higher states (viz. between the 22A0 and 32A0 electronically adiabatic potential energy surfaces), although this issue of multiple intersections is out of the scope of this work, it will not be discussed here any further. The major difference between the H3 and Li3 potential energy surfaces is the fact that the lower sheet of H3 is of the hat type and can support only resonance states. Moreover, these are mainly located in the collinear saddle-point region that is far from the conical intersection, which may explain why the GP effect calculated on the accurate H3 DMBE potential energy surface [82] is found [2] to play a minor role on such transition state resonances. Note further that the three equivalent saddle points are located on the outer circle that delimits the potential energy surface when this is viewed as a relaxed triangular plot [68] using hyperspherical coordinates, and are separated from each other by 2p=3. This feature is illustrated in Figure 11, which shows clearly the double-cone

~2 0 2 0

shape of the intersection between the X A and 2 A adiabatic potential energy surfaces near the degeneracy point (this corresponds to the structure with lowest energy along the D3h symmetry line).

As discussed in preceding sections, 1H and 3H have nuclear spin 12, which may have drastic consequences on the vibrational spectra of the corresponding trimeric species. In fact, the nuclear spin functions can only have A1 (quartet state) and E (doublet) symmetries. Since the total wave function must be antisymmetric, A1 rovibronic states are therefore not allowed. Thus, for J ¼ 0, only resonance states of A2 and E symmetries exist, with calculated states of A1 symmetry being purely ‘‘mathematical states.’’ Similarly, only E-symmetric pseudobound states are allowed for J ¼ 0. Indeed, even when vibronic coupling is taken into account, only A2 and E vibronic states have physical significance. Table XVII–XIX summarize the symmetry properties of the wave functions for 1H3 and its isotopomers.

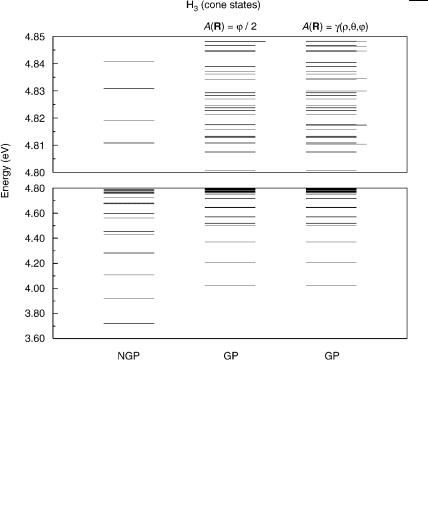
Calculations of bound vibrational levels have been carried out for the first electronically excited state of H3 with (and without) consideration of the GP effect using the GBO equation; [4,5,53], see Appendix A, Eq. (A.14). The