Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

686 a. j. c. varandas and z. r. xu

We now turn to some well-established cases where severe consequences arise due to the nuclear spin quantum number of the individual nuclei being 0 or 12. Consider the simplest case of spinless nuclei such as 16O2. Since the total wave function must be symmetric, it follows that only even rotational states are allowed for the ground vibrational state (this is always symmetric; see Section IX) when the electronic wave function is symmetric; conversely, only odd rotational states are allowed if the electronic wave function is antisymmetric. Since the ground electronic state of 16O2 is 3 g , and hence antisymmetric, it then follows that its lowest rotational state must have the rotation quantum number N ¼ 1, with one-half of the expected levels being absent in the corresponding Raman spectrum. Similarly, for transitions involving electronic states in homonuclear diatomic molecules with I ¼ 0, alternating lines will be missing in the rotational fine structure spectrum. If the nuclei are not identical (e.g., if one is 16O and the other is 17O), the above missing transitions will be restored.

A second well-known example is 1H2. Since the nuclear spin quantum number of 1H is 12, the total nuclear spin quantum number I can be 0 or 1. When I ¼ 0 the nuclear spin function is antisymmetric with respect to the interchange of the two protons. Conversely, the spin functions with I ¼ 1 are symmetric under the same operation. Since transitions between the I ¼ 0 and I ¼ 1 states are forbidden, one may view the hydrogen molecule as consisting of two distinct species: para-H2 with I ¼ 0, and ortho-H2 with I ¼ 1. The electronic ground state of H2 is a 1 þg state, and hence para-H2 can only possess rotational states with even or zero J values in order to preserve the antisymmetric nature of the total wave function; on the other hand, ortho-H2 will have only odd J rotational states. Of course, in statistical equilibrum at room temperature there will be three times as many H2 molecules in ortho states than in para states. As a result, the alternating lines in the rotational fine structure spectrum show a 3:1 intensity ratio. Such a ratio in the intensities of the rotational fine structure lines for a general homonuclear diatomic with nuclear spin quantum number I is ðI þ 1Þ=I: for bosons, it represents the relative statistical weight of symmetric to antisymmetric states; for fermions, the relative statistical weight of antisymmetric to symmetric states. Clearly, the nuclear statistical weights of rotational levels will affect the rotational partition function, and hence have implications in various fields such as thermodynamics and reaction kinetics. For linear molecules with identical nuclei that are interchangeable by rotation, the nuclear statistical weights can be calculated by the methods discussed in Section V.

^

Finally, let us consider molecules with identical nuclei that are subject to Cn

^

(n 2) rotations. For C2v molecules in which the C2 rotation exchanges two nuclei of half-integer spin, the nuclear statistical weights of the symmetric and antisymmetric rotational levels will be one and three, respectively. For

^

molecules where C2 exchanges two spinless nuclei, one-half of the rotational levels (odd or even J values, depending on the vibrational and electronic states)

will be missing. For symmetric and spherical tops, there are three or more identical nuclei interchangeable by rotation. For example, for the symmetric top methyl chloride (CH3Cl), the K ¼ 0; 3; 6; . . . rotational levels have twice the statistical weight of the K ¼ 1; 2; 4; . . . rotational levels for the symmetric vibronic states [56]. The rotational levels with different nuclear statistical weights must be summed over separately. However, for sufficiently high temperatures, it may be a good approximation to calculate the rotational partition function by giving to each rotational level an average statistical weight equal to the total spin multiplicity ð2IA þ 1Þð2IB þ 1Þ . . . ð2IZ þ 1Þ divided by a symmetry number that represents the number of different indistinguishable orientations obtained by proper rotations of the nuclear framework. For example, the symmetry numbers of C1v and D1h molecules are one and two, respectively. For nonlinear molecules, the symmetry number is equal to the order of the rotational subgroup, for example, 12 for both C6H6 and CH4.

IX. PERMUTATIONAL SYMMETRY OF VIBRATIONAL

WAVE FUNCTION

We now consider the permutational properties of the vibrational wave function. Similar to the discussion on the permutational symmetry for homonuclear diatomic molecules (and, in general, D1h molecules), in order to find the effect of interchanging the nuclei on the vibrational wave function we first invert the SF coordinates of the nuclei and all displacement vectors, and then carry out a back-inversion of the SF displacement vector coordinates alone. The net effect is therefore just the exchange of the SF coordinates of the nuclei. For D1h molecules, such an inversion of the nuclear coordinates exchanges all pairs of identical nuclei. Thus, the first inversion leaves the sign of the vibrational wave function unchanged for þ; þ; . . . vibrational states, while it changes its sign for ; ; . . . vibrational states. The second inversion classifies the vibrational wave functions in g or u according to whether the back-inversion of the displacement vectors leaves the wave function unchanged (the corresponding operator has a þ1 eigenvalue) or changes its sign (eigenvalue 1). We conclude that the vibrational wave functions are symmetric for þg ; u ; þg ; u ; . . .

vibrational states while being antisymmetric under permutation of identical nuclei for g ; þu ; g ; þu ; . . . vibrational states. Finally, we note that the ground vibrational states of homonuclear diatomics and, in general, D1h molecules are always symmetric under permutation of identical nuclei.

We now consider planar molecules. The electronic wave function is expressed with respect to molecule-fixed axes, which we can take to be the abc principal axes of inertia, namely, by taking the coordinates (x; y; z) in Figure 1 coincided with the principal axes (a; b; c). In order to determine the parity of the molecule through inversions in SF, we first rotate all the displacement vectors

and and nuclei (in their equilibrum positions) by 180 about the c axis (which is perpendicular to the molecular plane); and then reflect all the displacement vectors in the molecular ab plane. The first step has no effect on both the displacement vectors and the vibrational wave functions. The second step is a reflection of the displacement vectors in the molecular plane. Note that such a plane is a symmetry plane in this case, and the eigenvalues of the corresponding operator then determine the parity of the vibrational wave function. For a molecule with only in-plane vibrational modes, for example, H2O, the parity of the vibrational wave function is even. For BF3, there is a out-of-plane mode. The normal coordinate for such an out-of-plane mode is antisymmetric with respect to reflection in the molecular plane. Thus, the parities of the vibrational eigenfunctions of BF3 are determined by ð 1Þvn, where vn is the vibrational quantum number of the out-of-plane mode.

In order to determine the permutational symmetry of a nonlinear molecule, one can invoke the permutation group. The method is similar to that discussed in Section VI. We can see that the A2 vibrational state for a molecule of C3v geometry must be antisymmetric with an interchange of the two indentical nuclei. Similarly, the totally symmetric IRREPs in the point group always coorespond to [n] IRREPs in groups Sn. Let us consider the vibrational wave function of the electronic ground-state (B2) Li3. Noticing that the correlation between IRREPs of the group C2v and those of the group C2, and that the group C2 is isomorphic to the permutation group S2, one can say the B2 vibrational state must be antisymmetric with the interchange of the two indentical nuclei. Thus, for 7Li2 6Li and 6Li2 7Li, there are symmetric (A ½2& IRREP in the S2 permutation group) and antisymmetric (B ½12& in S2) vibrational states that are allowed by symmetry, and hence can be observed spectroscopically.

However, drastic consequences may arise if the nuclear spin is 0 or 12. In these cases, some rovibronic states cannot be observed since they are symmetry forbidden. For example, in the case of 12C16O2, the nuclei are spinless and the nuclear spin function is symmetric under permutation of the oxygen nuclei. Since the ground electronic state is þg , only even values of J exist for the ground vibrational level ðv1; vl22 ; v3Þ ¼ ð0000Þ, where ðv1; v2; v3Þ are the quantum numbers of symmetric stretching (n1), degenerate bending (n2), and antisymmetric stretching (n3) normal modes, respectively. As usual, l2 denotes the quantum number for vibrational angular momentum around the internuclear axis of the linear molecule in the degenerate vibrational mode n2, which can be shown to assume the values l2 ¼ v2; v2 2; . . . ; 1 or 0 (see Appendix D). Similarly, the vibrational mode n1 is þg , and hence the odd J rotational levels of the ð1000Þ vibrational state are missing, since they are antisymmetric. Following the same reasoning, the even J rotational levels of the ð0001Þ vibrational state will be missing due to the fact that the vibrational mode n3 has þu symmetry. Most severe consequences arise also when the total nuclear spin quantum

aAt minimum of the lower sheet of potential energy surface.

bRotation about the axis perpendicular to the plane of the molecule.

number is 12. For example, for the ground electronic state of 1H3 and 3H3 at J ¼ 0, the vibrational states of A1 symmetry will not be allowed and only the vibrational states of A2 and E symmetry can be observed.

As discussed above, the permutational symmetry of the total wave function requires the proper combination of its various contributions. These are summarized in Tables V–XII for all isotopomers of Li3. Note that the conclusions hold provided that the various wave functions have the appropriate symmetries. If, for some reason, one of the components fails to meet such a requirement, then the symmetry of the total wave function will fail too. For example, even if the vibrational wave functions are properly assigned, the total wave

aAt minimum of the conical intersection on the upper sheet of potential energy surface.

bRotation about the axis perpendicular to the plane of the molecule.

aAt minimum of the lower sheet of potential energy surface.

bRotation about the axis perpendicular to the plane of the molecule.

aAt minimum of the conical intersection on the upper sheet of potential energy surface.

bRotation about the axis perpendicular to the plane of the molecule.

TABLE IX

The Symmetry Properties of Wave Functions of 7Li2 6Li Electronically Ground State

in S2 Permutation Group

aAt minimum of the lower sheet of potential energy surface.

bRotation about the axis through the 6Li and perpendicular to the 7Li2.

aAt minimum of the conical intersection on the upper sheet of potential energy surface.

bRotation about the axis through the 6Li and perpendicular to the 7Li2.

TABLE XI

The Symmetry Properties of Wave Functions of 6Li2 7Li Electronically Ground State

in S2 Permutation Group

aAt minimum of the lower sheet of potential energy surface.

bRotation about the axis through the 7Li and perpendicular to the 6Li2.

TABLE XII

The Symmetry Properties of Wave Functions of 6Li2 7Li Electronically First-Excited State

in S2 Permutation Group

aAt minimum of the conical intersection on the upper sheet of potential energy surface.

bRotation about the axis through the 7Li and perpendicular to the 6Li2.

function of systems with conical intersections such as Li3 may have no physical significance due to failure of the electronic wave function to meet the requirement of single valuedness (i.e., no change of sign when traversing a path that encircles the crossing point). In other words, one needs to include GP effects or treat the dynamics more accurately (e.g., by solving the 2 2 coupled

state dynamics problem) in order to warrant the correct symmetry properties of the total wave function. This will be further discussed in Section X.

X.CASE STUDIES: Li3 AND OTHER 2S SYSTEMS

A.Potential Energy Surfaces

H3 (and its isotopomers) and the alkali metal trimers (denoted generally for the homonuclears by X3, where X is an 2S atom) are typical Jahn–Teller systems where the two lowest adiabatic potential energy surfaces conically intersect. Since such manifolds of electronic states have recently been discussed [60] in some detail, we review in this section only the diabatic representation of such surfaces and their major topographical details. The relevant 2 2 diabatic potential matrix W assumes the form

where W12 ¼ W21. Specifically, for H3 and Li3, two systems that we discuss in detail in this chapter, the matrix elements in Eq. (54) are written as [61]

where the Q and J values are the well-known Coulomb and exchange integrals that can be obtained semiempirically [62–65] from the lowest singlet and triplet diatomic potential curves, XEHFð3Þ is a three-body extended Hartree–Fock type energy, and Vdc the total dynamical correlation energy. Note that the prime in the Q and J parameters express the fact that such quantities are calculated from the extended Hartree–Fock curves alone [61].

Diagonalization of W then leads to the two adiabatic surfaces

which may cross when W11 ¼ W22 and W12 ¼ 0. For X3 systems, such a crossing seam is representative of a so-called conical intersection: For a fixed

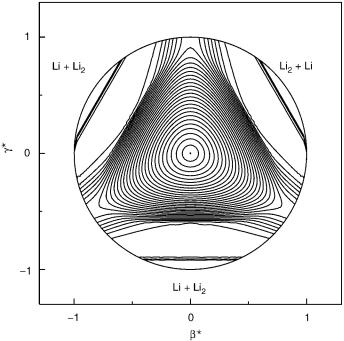
surface of an upper one-half of the sphere. The b? coordinate is associated to sinðy=2Þcosj, while g? denotes sinðy=2Þsinj. The hyperangle y runs from zero at the north pole (center of plot) to p=2 at the equator (the outside circle). The hyperangle j is measured from the positive g? axis and grows on going counterclockwise. For the lower sheet, it is noted that the lowest point along the D3h conical intersection seam is located at the origin of the plot and corresponds to an equilateral triangular configuration. As can be seen, the threefold symmetry gives rise to three wells that are equally spaced by 120 intervals around the origin. The minimum energy of the barrier for pseudorotation relative to the bottom of such wells (i.e., the height of the saddle points between the three wells), and the energy of the lowest point along the conical intersection seam are6 0.4 meV and 0.0542 eV, respectively. Note that the motion along the hyperradius r corresponds to the symmetric stretching mode. Moreover, at the bottom of the well just above the origin, motion along the g? axis corresponds to the bending mode while motion along the b? axis corresponds to the antisymmetric stretching mode. In addition, motion along the hyperangle j about the origin corresponds to the pseudorotational motion. Finally, note that the origin in the plot of the upper sheet corresponds to an equilateral triangular geometry.

B.Static Jahn–Teller Effect

Now, we examine the effect of vibronic interactions on the two adiabatic potential energy surfaces of nonlinear molecules that belong to a degenerate electronic state, so-called static Jahn–Teller effect.

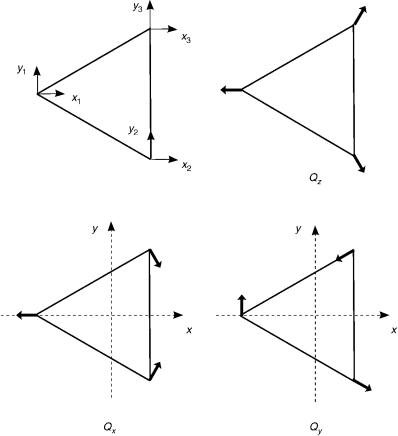
For a X3 molecule in the D3h symmetry point group, we have a totally symmetric A01 and a doubly degenerate E0 vibrational normal modes in the harmonic-oscillator approximation as illustrated in Figure 5. However, for a real molecule that vibrates anharmonically, we must consider the effects due to anharmonicity. As discussed in Appendix D, we must then use the set of quantum numbers ðv1; v2; l2Þ instead of ðv1; v2a; v2bÞ, and employ the notation ðv1; vl22 Þ to label the vibrational levels; l2 is the vibrational angular momentum quantum number with respect to the symmetry axis. Table XIII gives the assignments of the lowest vibrational levels for Li3 in the D3h symmetry point group. From this assignment, one can determine the symmetry of the level. For example, the ground vibrational state ð0; 00Þ is A01 and the level ð1; 11Þ is E0, since v1 is totally symmetric and A01 ! E0 ¼ E0. In turn, for multiply excited

degenerate vibrations [28,59], the symmetry A01 corresponds to l2 ¼ 0, A01 A02 to l2 ¼ 3; 6; . . . and E0 to l2 ¼ 1; 2; 4; 8; . . . ; note that l2 is a good quantum number, and hence can be used to specify the symmetry of the vibrational level.

For example, the level ð0; 31Þ has E0 symmetry while ð0; 33Þ is A01 A02. Also

Figure 5. Definition of the normal mode coordinates for a D3h X3 molecule.

note that anharmonicity splits the degeneracy of the vibrational levels obtained in the harmonic approximation [28].

We now take vibronic interactions into account. In this case, we must determine vibronic states rather than the electronic and vibrational ones. For example, if X3 in a degenerate E0 vibration is singly excited in an E0 electronic state, we obtain the vibronic states evA01 evA02 evE0, since vE0 ! eE0 ¼ evA01 evA02 evE0. If the same vibration is doubly excited (e.g., if v2 ¼ 2, with the symmetric product being ½vE0 !v E0& ¼ vA01 vE0: Note that the associated antisymmetric product is vA02), we get the vibronic species ðvA01 vE0Þ ! eE0 ¼ evA01 evA02 2evE0. Table XIII shows the symmetries of the lowest 25 vibrational and vibronic states. In turn, the lowest 26 levels calculated for Li3