Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

where Fji ðq=qxjÞni is computed by divided difference and x ¼ ða; b; gÞ. The properties of the solutions of Eq. (20) will be discussed in Section III.

that span the branching space. The associated coordinates (x; y; z) are referred to as orthogonal intersection adapted coordinates.

2.A Transformational Invariant

In the nonrelativistic case, at a given Rx;IJ , the quantity gIJ hIJ was shown to be invariant under the transformation in Eq. (16), for a ¼ g ¼ 0. This invariant, whose value depends on Rx;IJ , was used to systematically locate confluences, [18–21], intersection points at which two distinct branches of the conical

intersection seam intersect. Here, we show that the scalar triple product, gij hr;ij hi;ij is the invariant for Z ¼ 3. Since the gij; hr;ij, and hi;ij cannot be

assumed orthogonal the scalar triple product has the following form (suppressing the ij superscripts)

g hr hi ¼ ðgxi þ gy j þ gzkÞ ðhrxi þ hry j þ hrzkÞ ðhixi þ hiy j þ hizkÞ

To demonstrate the invariance insert, Eqs. (17a), (17c), and (17d) into Eq. (21) giving

~ ¼ ~ ~r ~i

I g h h

¼fðhrxhiy hryhixÞðsin b sin aÞ þ ð gxhiy þ gyhixÞðcos a sin g þ cos g cos b sin aÞ

þðgxhry gyhrxÞð cos a cos g þ cos b sin a sin gÞgf gzsin b sin a

hrzðsin g cos a þ cos b sin a cos gÞ hizðcos b sin a sin g cos g cos aÞg

þcyclic permutations

¼fð hrxhiy þ hryhixÞgz þ ðhryhiz hrzhiyÞgx þ ðhixhrz hizhrxÞgygfðsin2b sin2aÞ

þðcos a sin g þ cos g cos b sin aÞ2 þ ðcos b sin asin g cos g cos aÞ2g

The use of this invariant is discussed in Section III.

3.Local Topography: Energy

The topography of a conical intersection affects the propensity for a nonadiabatic transition. Here, we focus on the essential linear terms. Higher order effects are described in [10]. The local topography can be determined from Eq. (13). For Z ¼ 3, Eq. (13) becomes, in orthgonal intersection adapted coordinates

where I is a 2 2 unit matrix, and the r are the Pauli matrices.

To determine the eigenfunctions and eigenvalues of Eq. (23), it is convenient

where MijðxÞ ¼ dijðxd1j þ x d2jÞ. This Hamiltonian can be diagonalized by the transformation

From the preceding analysis, it is seen that the coordinate space near Rx;ij can be usefully partitioned into the branching space described in terms of intersection adapted coordinates ðr; y; fÞ or (x; y; z) and its orthogonal complement the seam space spanned by a set of mutually orthonormal set wi; i ¼ 4 Nint. From Eq. (27), spherical radius r is the parameter that lifts the degeneracy linearly in the branching space spanned by ^x; ^y; and ^z.

570 spiridoula matsika and david r. yarkony

Note that since the eigenfunctions are determined only up to an overall phase, the

As discussed in detail in [10], equivalent results are not obtained with these three unitary transformations. A principal difference between the U; V, and B results is the phase of the wave function after being transported around a closed loop C, centered on the z axis parallel to but not in the (x; y) plane. The perturbative wave functions obtained from Uðy; fÞ or Bðy; fÞ are, as seen from Eq. (26a) or (26c), single-valued when transported around C that is h ei ðr; R0Þj ei ðr; RnÞi ¼ 1, where R0 ¼ Rn denote the beginning and end of this loop. This is a necessary condition for Berry’s geometric phase theorem [22] to hold. On the other hand, the perturbative wave functions obtained from V(y; f) in Eq. (26b) are not single valued when transported around C.

U, V, and B also yield different fkk. By using Eqs. (24a)–(24d) and (26a) the derivative couplings are

From Eqs. (30a)–(30c), the singularity in fkl, as the conical intersection is approached, is of order 1=r. Only foij; o ¼ y; f are singular [10]. As in the nonrelativistic case, knowledge of the singular part of the derivative coupling can be used to construct a local diabatic representation that removes the singularity

[10].

If Vðy; fÞ had been used in lieu of Uðy; fÞ; jfij;ð0Þj would be unchanged, but fkk;ð0Þ becomes fkk;ð0Þ;V , which is given by

Finally, had Bðy; fÞ been used, fii;ð0Þ would be unchanged, but

symmetry, 2E0 3E0, intersection to illustrate the ideas developed in Section 2.F.5. This system provides a stringent test of the numerical procedures since the spin–orbit interaction is relatively modest and the energy splitting changes rapidly in the region of interest.

The nonrelativistic states are described at the first-order configuration interaction level using a six orbital, eight electron, active space with the oxygen 1s orbital kept doubly occupied. The molecular orbitals were constructed from a state-averaged multiconfigurational self-consistent field procedure [31] using an extended atomic orbital basis on oxygen and hydrogen. The details of this description can be found in [30].

In the present calculations, the molecule is restricted to Cs symmetry. There are five internal degrees of freedom (the out-of-plane mode is excluded

to preserve Cs symmetry). Nuclear configurations will be denoted R ¼ ðRðH1 OÞ; RðO H2Þ; RðH2 H3Þ; H1OH2; OH2H3Þ corresponding to the

arrangement H1 O H2 H3. It will be convenient to refer to the R by their RðH2 H3Þ value, writing, RðRðH2 H3Þ ¼ bÞ RðbÞ ¼ ðRðH1 OÞ; RðO H2Þ; RðH2 H3Þ ¼ b; H1OH2; OH2H3Þ. For collinear geometries, the two angles will be suppressed. Equation (14) defines only three internal coordinates. Therefore two additional constraints are needed. These are provided by the value of RðH2 H3Þ ¼ b and/or the energy minimization requirement.

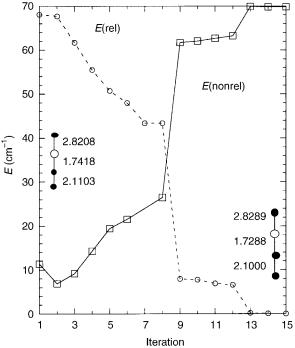
B.Convergence of Eq. (15b)

Figure 2 illustrates the efficacy of Eq. (15), considering convergence, in the absense of geometrical constraints, to a local energy minimum on the relativistic seam of conical intersection. Reported are the relativistic energy separation E32e and the nonrelativistic energy separation, E22A0;12A0 . The search was initiated at the structure indicated on the left-hand side of Figure 2, a point slightly displaced from the nonrelativistic seam. At this point, E22A0;12A0 11 cm 1 andE32e 70 cm 1. At the converged structure, achieved after 15 iterations,

pictured on the right-hand side, E32e < 0:2 cm 1 while E22A0;12A0 70 cm 1. The large changes in E32e between iterations 8 and 9, and 12 and 13, reflect, in

part, the use of the ‘‘conjugate gradient’’ extrapolation noted previously. These results strongly support the utility of the present approach. It is worth noting that once an initial point on a seam is found locating additional points is facilitated by the fact that given an Rx;ij corresponding to given K, Eq. (15b) can be used to predict a good starting value for a neighboring Rx;ij0 corresponding to K0 [32].

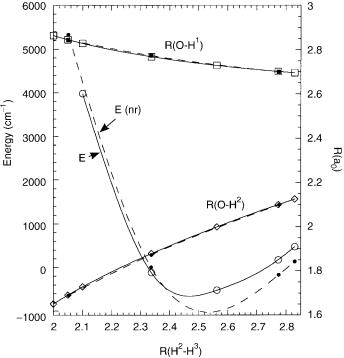
C.The Seam: Locus

Further evidence of the efficacy of the algorithm for locating points of conical intersection is provided in Figure 3, which reports additional points on the 2E0– 3E0 intersection seam, determined by introducing the geometrical constraint,

RðH2 H3Þ ¼ b. Note that C1v symmetry was not imposed. The points located on the 2E0–3E0 seam of conical intersection, which are degenerate to <1 cm 1, all had C1v symmetry. Figure 3 shows, that while the Z ¼ 3 seam is necessarily distinct from the nonrelativistic seam the separation is not large. In future work, it will be interesting to see how this conclusion changes as the magnitude of the spin–orbit interaction increases. Along the nonrelativistic seam the relativistic

fine structure splitting [33] suggesting that when heavier atoms such a chlorine,

significantly reduced at the nonrelativistic seam by the inclusion of spin–orbit coupling.

intersection of H . However, since numerical degeneracies are never exact, an

Figure 3. The relativistic seam Rx;ijðRðH2 H3ÞÞ: RðO–H1Þ, (empty squares), RðO H2Þ (empty diamonds) E E2E0 ðRðH2 H3ÞÞ (empty circles) on the 2E 3E seam of conical intersection. Filled markers on 12A0 22A0 nonrelativistic seam of conical intersection. The zero of energy is EðnrÞ E12A0 ðRx;IJðRðH2 H3Þ ¼ 2:336ÞÞ ¼ 76:486688 a.u.

alternative means is required to prove the existence of a conical intersection. The demonstration that g hr hi ¼6 0, that is, that g; hr; hi are linearly independent, serves to confirm the ‘‘conical’’ character near the intersection. It is to the determination of these quantities that we now turn.

D. The Seam: Conical Parameters and the Invariant

The lowest order contributions to the energy are described by the conical parameters g; hr; hi, and sk; k ¼ x; y; z, or by d; i ¼ 1; 2 and sk; k ¼ x; y; z. Here and below the superscript ij is suppressed when no confusion will result. We also will use the nonrelativistic convention gijjj^x; hr;yjj^y and hi;ijjj^z, where jj is real ‘‘is parallel to.’’ These parameters [9] are reported in Figure 4a and b. Their continuity is attributable to the use of orthogonal intersection adapted coordinates. For comparison, Figure 4a and b reports the nonrelativistic quantities gIJ ; hIJ , and sIJ , respectively. While noting that there is no unique correspondence