
Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)
.pdf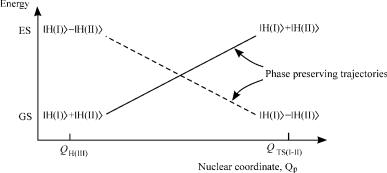
conical intersections in molecular photochemistry |
445 |
configuration (point in phase space) is reached, in which it changes sign. This ‘‘point’’ is the out-of-phase transition state. The same holds for the electronic wave function of the excited state. The two potential curves cross at some point, where the electronic wave function becomes degenerate. The crossing along this coordinate is permitted, since the two curves are of different symmetry.
This situation arises when the electronic wave function of the transition state is described by the out-of-phase combination of the two base functions. If the electronic wave function of the transition state is described by the in-phase combination, no curve crossing occurs.
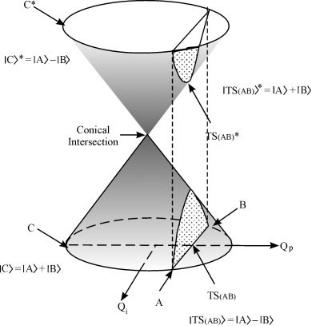
In the vicinity of the crossing point of the two electronic states of the H4 system, we can therefore define two coordinates along which the potential surface of the system is constructed. The phase-preserving coordinate Qp connecting the H(I) minimum with TS(II–III), and the phase-inverting coordinate Qi connecting the minima of H(II) and H(III). A plot of the energies of the two surfaces has the shape of double cone. Moreover, as nothing but spin pairing was assumed in the derivation, the situation is not unique to the H4 system: It holds for any four-electron system. Figure 6 depicts the general case, in which the potential energy surface relevant to three chemical species A, B,
Figure 6. A schematic representation of a conical intersection. The bottom part of the cone belongs to the ground state, the upper, to the electronically excited state.
446 |
yehuda haas and shmuel zilberg |
and C is shown. The species A, B, and C consist of the same atoms, and differ only in their spin pairing schemes. We assume that the electronic wave function of C, jCi, may be expressed as the in-phase combination of jAi and jBi, while the transition state between A and B TS(AB) is represented by the out-of-phase combination. Here C is a local minimum on the ground-state surface. At the geometry of the transition state, the in-phase combination of jAi and jBi lies on the excited potential surface.
The H4 system is the prototype for many four-electron reactions [34]. The basic tetrahedral structure of the conical intersection is preserved in all fourelectron systems. It arises from the fact that the four electrons are contributed by four different atoms. Obviously, the tetrahedron is in general not a perfect one. This result was found computationally for many systems (see, e.g., [37]). Robb and co-workers [38] showed that the structure shown (a tetraradicaloid conical intersection) was found for many different photochemical transformations. Having the form of a tetrahedron, the conical intersection can exist in two enantiomeric structures. However, this feature is important only when chiral reactions are discussed.
The two coordinates defined for H4 apply also for the H3 system, and the conical intersection in both is the most symmetric structure possible by the combination of the three equivalent structures: An equilateral triangle for H3 and a perfect tetrahedron for H4. These structures lie on the ground-state potential surface, at the point connecting it with the excited state. This result is generalized in the Section. IV.
III.PHASE CHANGE IN A CHEMICAL REACTION
The phase change occurring upon carrying out a complete loop around a point, as discussed by Longuet-Higgins and Herzberg, does not explicitly consider phase changes in chemical reactions. However, the proof concerning H3 depends on the phase change taking place during the methathesis reaction H1H2 þ H3 ! H1 þ H2H3 [12]. In this section, we discuss the general case—a phase change taking place upon an arbitrary chemical reaction.
A chemical reaction takes place on a potential surface that is determined by the solution of the electronic Schro¨dinger equation. In Section, we defined an anchor by the spin-pairing scheme of the electrons in the system. In the discussion of conical intersections, the only important reactions are those that are accompanied by a change in the spin pairing, that is, interanchor reactions. We limit the following discussion to these class of reactions.
The concept of phase change in chemical reactions, was introduced in Section I, where it was shown that it is related to the number of electron pairs exchanged in the course of a reaction. In every chemical reaction, the fundamental law to be observed is the preservation permutational symmetry of
conical intersections in molecular photochemistry |
447 |
the polyelectronic wave function: Pauli’s principle must be obeyed. Phase changes are not generally regarded as important parameters in understanding the fundamentals of chemical reactions. Goddard tried to utilize the phasechange concept for a better understanding of chemical transformations [22,39]. Up to now, these efforts do not seem to have significantly affected the way chemists conceive reactions. We propose that the study of phase change in chemical reaction may become a substantial ingredient in photochemical theory, since conical intersections appear to be of major importance in this field. The phase-change rule is closely related to conical intersections on one hand, and to the phase change on the other. We suggest that a loop can always be constructed from several reactions, and the total phase change deduced from the combination of changes incurred in the individual steps [25,40,41]. If this hypothesis proves to be correct, phase changes taking place on the ground-state surface will play an important role in photochemistry.
In this section, we illustrate the applicability of the model to some important special cases, and summarize the relationship between aromaticity and chemical reactivity, expressed in the properties of transition states.
A.Pericyclic Reactions
The special case of pericyclic reactions is an appropriate means of introducing the subject: These reactions are very common, and were extensively studied experimentally and theoretically. They also provide a direct and straightforward connection with aromaticity and antiaromaticity, concepts that turn out to be quite useful in analyzing phase changes in chemical reactions.
Already in 1938, Evans and Warhurst [17] suggested that the Diels–Alder addition reaction of a diene with an olefin proceeds via a concerted mechanism. They pointed out the analogy between the delocalized electrons in the transition states for the reaction between butadiene and ethylene and the p electron system of benzene. They calculated the resonance stabilization of this transition state by the VB method earlier used by Pauling to calculate the resonance energy of benzene. They concluded that the extra ‘‘aromatic’’ stabilization of this transition state made the concerted route more favorable then a two-step process. In a subsequent paper [18], Evans used the Hu¨ckel MO theory to calculate the transition state energy of the same reaction and some others. These ideas essentially introduce a chemical reacting complex (reactants and products) as a two-state system. Dewar [42] later formulated a general principle for all pericyclic reactions (Evans’ principle): Thermal pericyclic reactions take place preferentially via aromatic transition states. Aromaticity was defined by the amount of resonance stabilization. Evans’ principle connects the problem of thermal pericyclic reactions with that of aromaticity: Any theory of aromaticity is also a theory of pericyclic reactions [43]. Evans’ approach was more recently used to aid in finding conical intersections [44], (cf. Section VIII).
448 yehuda haas and shmuel zilberg
Several theories of aromaticity have been suggested, starting with Hu¨ckel’s 4n þ 2 rule [29]. All of them consider the entities in question as two-state systems (Section I), and consider the relative phase relations of adjacent p orbitals as playing a major role. It has been pointed out by many authors [19,21,45–47] that in a conjugated systems there can be two cases. If all neighboring lobes of p- orbitals have a the same sign, the system is denoted as a Hu¨ckel one. If, on the other hand, there is a phase change at one point (termed phase dislocation by Craig [46]), the system is a Mo¨bius one (one of the p orbitals is inverted by 180 , forming a Mo¨bius strip). This definition may be generalized [19]: In a Hu¨ckel system, the number of dislocations is even, in a Mo¨bius system, it is odd. Mo¨bius systems are sometimes termed anti-Hu¨ckel.
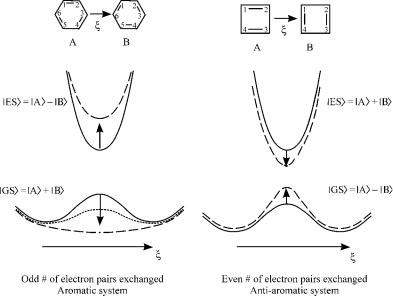
A more general classification considers the phase of the total electronic wave function [13]. We have treated the case of cyclic polyenes in detail [28,48,49] and showed that for Hu¨ckel systems the ground state may be considered as the combination of two Kekule´ structures. If the number of electron pairs in the system is odd, the ground state is the in-phase combination, and the system is aromatic. If the number of electron pairs is even (as in cyclobutadiene, pentalene, etc.), the ground state is the out-of-phase combination, and the system is antiaromatic. These ideas are in line with previous work on specific systems [40,50].
The results of the derivation (which is reproduced in Appendix A) are summarized in Figure 7. This figure applies to both reactive and resonance stabilized (such as benzene) systems. The compounds A and B are the reactant and product in a pericyclic reaction, or the two equivalent Kekule´ structures in an aromatic system. The parameter x is the reaction coordinate in a pericyclic reaction or the coordinate interchanging two Kekule´ structures in aromatic (and antiaromatic) systems. The avoided crossing model [26–28] predicts that the two eigenfunctions of the two-state system may be formed by in-phase and out- of-phase combinations of the noninteracting basic states jAi and jBi. State jAi differs from jBi by the spin-pairing scheme.
The ground state is the in-phase combination ðjAi þ jBiÞ for an odd number of electron pairs exchanged, while if the number is even, the out-of-phase ðjAi jBiÞ combination is the ground state. The other combination is an electronically excited state. Classical VB theory predicts the curves shown as solid lines. The energy ordering of the in-phase and out-of-phase combinations, and the energy splitting between them is due primarily to the pairwise transposition permutations (Appendix A). The effect of the cyclic permutation term [32], shown by the dashed lines, is to modify the splitting: In systems for which an odd number of electron pairs are exchanged, the cyclic permutation term acts in harmony with the classical term, and increases the gap between the ground and excited state. In the even parity systems, it acts to decrease the gap. When the cyclic term is large enough, a single minimum in the ground state is obtained—this is the origin of the extra stability of benzene, for example. In
conical intersections in molecular photochemistry |
449 |
Figure 7. Aromatic and antiaromatic systems in the ground state (GS) and the twin excited state (ES). The parameter x is the coordinate that transforms A to B.
other systems, the barrier is reduced but not eliminated. The result is a stabilized aromatic transition state [51].
Adopting the view that any theory of aromaticity is also a theory of pericyclic reactions [19], we are now in a position to discuss pericyclic reactions in terms of phase change. Two reaction types are distinguished: those that preserve the phase of the total electronic wave-function – these are phase preserving reactions (p-type), and those in which the phase is inverted – these are phase inverting reactions (i-type). The former have an aromatic transition state, and the latter an antiaromatic one. The results of [28] may be applied to these systems. In distinction with the cyclic polyenes, the two basis wave functions need not be equivalent. The wave function of the reactants jRi and the products jPi, respectively, can be used. The electronic wave function of the transition state may be represented by a linear combination of the electronic wave functions of the reactant and the product. Of the two possible combinations, the in-phase one [Eq. (11)] is phase preserving (p-type), while the out-of-phase one [Eq. (12)], is i-type (phase inverting), compare Eqs. (6) and (7). Normalization constants are assumed in both equations:
jAromatic TSi ¼ jAi þ jBi |
Phase-preserving transition state |
ð11Þ |
jAntiaromatic TSi ¼ jAi jBi |
Phase-inverting transition state |
ð12Þ |
450 |
yehuda haas and shmuel zilberg |
The Woodward–Hoffmann method [52], which assumes conservation of orbital symmetry, is another variant of the same idea. In it, the emphasis is put on the symmetries of molecular orbitals. Longuet-Higgins and Abramson [53] noted the necessity of state-to-state correlation, rather than the orbital correlation, which is not rigorously justified (see also, [30,44]). However, the orbital symmetry conservation rules appear to be very useful for most thermal reactions.
A symmetry that holds for any system is the permutational symmetry of the polyelectronic wave function. Electrons are fermions and indistinguishable, and therefore the exchange of any two pairs must invert the phase of the wave function. This symmetry holds, of course, not only to pericyclic reactions.
B.Generalization to Any Reactions
In this chapter, we restrict the discussion to elementary chemical reactions, which we define as reactions having a single energy barrier in both directions. As discussed in Section I, the wave function jRi of any system undergoing an elementary reaction from a reactant A to a product B on the ground-state surface, is written as a linear combination of the wave functions of the reactant, jAi, and the product, jBi [47,54]:
jRi ¼ CAjAi þ CBjBi |
ð13Þ |
CA and CB may have the same or opposite signs.
Within the Born–Oppenheimer approximation, the electronic wave function jRiel, is well defined, throughout the reaction and may be written analogously [cf. Eq. (6)]
jRðtÞiel ¼ kAðtÞjAiel þ kBðtÞjBiel |
ð14Þ |
where kA is unity in the beginning of the reaction (t ¼ 0) and kB is unity at the end (t ¼ 1) [26]. A phase change involves the introduction of a new node (or an odd number of nodes) along the reaction coordinate, which is equivalent to changing the total electronic angular momentum of the system along that coordinate. The role of nodes and nodal parity was discussed extensively for correlated molecular orbitals during a reaction [21]. A similar approach, using VB, was suggested by Mulder and Oosterhof for pericyclic reactions [32]. We emphasize the properties of the total wave function, a concept that is difficult to visualize in a graphic manner.
There are two mechanisms by which a phase change on the ground-state surface can take place. One, the orbital overlap mechanism, was extensively discussed by both MO [55] and VB [47] formulations, and involves the creation of a negative overlap between two adjacent atomic orbitals during the reaction (or an odd number of negative overlaps). This case was termed a phase dislocation by other workers [43,45,46]. A reaction in which this happens is
conical intersections in molecular photochemistry |
451 |
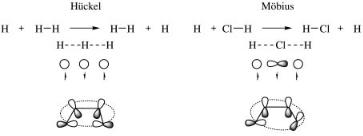
termed Mo¨biusor anti-Hu¨ckel type. A well-known example is conrotatory ring closure in pericyclic reactions. Another is the antarafacial sigmatropic migration. A reaction in which all overlaps between adjacent atomic orbitals along the reaction coordinate are positive (or such that the number of negative overlaps is even) is termed Hu¨ckel type. Only Hu¨ckel-type reactions are possible when s orbitals are the sole ones involved in the reaction. With p orbitals, both Hu¨ckeland Mo¨bius-type reactions are possible. Figure 8 depicts two examples.
The second mechanism, due to the permutational properties of the electronic wave function is referred to as the permutational mechanism. It was introduced in Section I for the H4 system, and above for pericyclic reactions and is closely related to the aromaticity of the reaction. Following Evans’ principle, an aromatic transition state is defined in analogy with the hybrid of the two Kekule´ structures of benzene. A cyclic transition state in pericyclic reactions is defined as aromatic or antiaromatic according to whether it is more stable or less stable than the open chain analogue, respectively. In [32], it was assumed that the inphase combination in Eq. (14) lies always the on the ground state potential. As discussed above, it can be shown that the ground state of aromatic systems is always represented by the in-phase combination of Eq. (14), and antiaromatic ones—by the out-of-phase combination.
The concepts may be extended to describe transition states of any chemical reaction. Since the only assumption made was that the VB structures represent the molecules, and that an exchange of two columns in the determinant representing the VB structures changes the sign, the result is general (Appendix A).
Figure 8. Hu¨ckel and Mo¨bius reactions. Top left: the H þ H2 reaction. The second line shows the structure of the linear transition state, the circles in the third line denote s-type orbitals, the arrows designate the electron spin vectors. Top right: the H þ ClH reaction. The second line shows the structure of the linear transition state, the symbols in the third line denote s- and p-type orbitals, the arrows designate the electron spin vectors. Bottom left: A disrotatory ring closure reaction of butadiene, showing the p-orbitals of the carbon atoms that exchange the spin-pairs. Bottom right: A conrotatory ring closure reaction of butadiene, showing one negative overlap between p-orbitals of the carbon atoms that exchange the spin-pairs.

452 |
yehuda haas and shmuel zilberg |
We term the in-phase combination an aromatic transition state (ATS) and the out-of-phase combination an antiaromatic transition state (AATS). An ATS is obtained when an odd number of electron pairs are re-paired in the reaction, and an AATS, when an even number is re-paired. In the context of reactions, a system in which an odd number of electrons (3, 5, . . .) are exchanged is treated in the same way—one of the electron pairs may contain a single electron. Thus, a three-electron system reacts as a four-electron one, a five-electron system as a six-electron one, and so on.
Finally, the distinction between Hu¨ckel and Mo¨bius systems is considered. The above definitions are valid for Hu¨ckel-type reactions. For aromatic Mo¨biustype reations, the reverse holds: An ATS is formed when an even number of electron pairs is re-paired.
These general ideas will be demonstrated by considering a few examples.
1.Reactions Involving Sigma Bonds Only
The H3 and H4 systems were discussed above. Another type of sigma bonds involves a p orbital lying along the reaction coordinate, as, for example, in reaction (15) (Fig. 8).
H þ ClH ! HCl þ H |
ð15Þ |
This is an example of a Mo¨bius reaction system—a node along the reaction coordinate is introduced by the placement of a phase inverting orbital. As in the H þ H2 system, a single spin-pair exchange takes place. Thus, the reaction is phase preserving. Mo¨bius reaction systems are quite common when p orbitals (or hybrid orbitals containing p orbitals) participate in the reaction, as further discussed in Section III.B.2.
A phase change takes place when one enantiomer is converted to its optical isomer. As illustrated in Figure 9, when the chiral center is a tetra-substituted carbon atom, the conversion of one enantiomer to the other is equivalent to the exchange of two electron pairs. This transformation is therefore phase inverting.
2.Reactions Involving p Bonds
Hu¨ckel-type systems (such as Hu¨ckel pericyclic reactions and suprafacial sigmatropic shifts) obey the same rules as for sigma electron. The rationale for this observation is clear: If the overlap between adjacent p-electron orbitals is positive along the reaction coordinate, only the permutational mechanism can
|
L |
|
|
L |
|
|
4 |
3 |
|
|
3 |
2 |
|
O |
|
|
||||
C |
M |
M |
C |
|||
N |
||||||
|
1 |
1 |
||||
2 N |
|
|
4 O |
|
||
Figure 9. The phase-inverting transformation of a |
{12,34} |
|
|
{14,23} |
|
|
chiral system with a tetra-substituted carbon atom. |
|
|
|
|||
conical intersections in molecular photochemistry |
453 |
lead to sign inversion. In Mo¨bius-type systems (antarafacial reactions), the system will change phase only if an even number of electron spin pairs exchanges takes place.
Electrocyclic reactions are examples of cases where p-electron bonds transform to sigma ones [32,49,55]. A prototype is the cyclization of butadiene to cyclobutene (Fig. 8, lower panel). In this four electron system, phase inversion occurs if no new nodes are formed along the reaction coordinate. Therefore, when the ring closure is disrotatory, the system is Hu¨ckel type, and the reaction a phase-inverting one. If, however, the motion is conrotatory, a new node is formed along the reaction coordinate just as in the HCl þ H system. The reaction is now Mo¨bius type, and phase preserving. This result, which is in line with the Woodward–Hoffmann rules and with Zimmerman’s Mo¨bius–Hu¨ckel model [20], was obtained without consideration of nuclear symmetry. This conclusion was previously reached by Goddard [22,39].
IV. LOOP CONSTRUCTION FOR
PHOTOCHEMICAL SYSTEMS
In this section, the systematic search for conical intersections based on the Longuet-Higgins phase-change rule is described. For conciseness sake, we limit the present discussion to Hu¨ckel-type systems only, unless specifically noted otherwise. The first step in the analysis is the determination of the LH loops containing a conical intersection for the reaction of interest.
In general, at least three anchors are required as the basis for the loop, since the motion around a point requires two independent coordinates. However, symmetry sometimes requires a greater number of anchors. A well-known case is the Jahn–Teller degeneracy of perfect pentagons, heptagons, and so on, which will be covered in Section V. Another special case arises when the electronic wave function of one of the anchors is an out-of-phase combination of two spinpaired structures. One of the vibrational modes of the stable molecule in this anchor serves as the out-of-phase coordinate, and the loop is constructed of only two anchors (see Fig. 12).
We have seen (Section I) that there are two types of loops that are phase inverting upon completing a round trip: an i3 one and an ip2 one. A schematic representation of these loops is shown in Figure 10. The other two options, p3 and i2p loops do not contain a conical intersection. Let us assume that A is the reactant, B the desired product, and C the third anchor. In an ip2 loop, any one of the three reaction may be the phase-inverting one, including the B ! C one. Thus, the A ! B reaction may be phase preserving, and still B may be attainable by a photochemical reaction. This is in apparent contradiction with predictions based on the Woodward–Hoffmann rules (see Section VIII). The different options are summarized in Figure 11.
