Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский национальный исследовательский технологический университет

Предмет:

Химия

Файл:

Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

.pdf

Скачиваний:

Добавлен:

15.08.2013

Размер:

4.29 Mб

Скачать

☆

<<< < Предыдущая 36 37 38 39 40 41 42 43 44 45 46 4748 / 8248 49 50 51 52 53 54 55 56 57 58 59 60 > Следующая >>>

524

k. k. liang et al.

N1N2

ð 1 dt

ð 1 dx xn1 ðx þ XÞn2 e ða1þa2þt

Þx

2a2Xx a2X

e ð

2a2Yy

a2Y2

ð 1 dy y

ðy þ YÞ

ð 1 dz zm1 ðz þ ZÞm2 e ða1þa2þt

Þz

2a2Zz a2Z

N1N2

2 1

2 2

ð 1dt e a2R

ð 1dx xn1 ðx þ XÞn2 e ða1þa2þt

Þ½xþa2X=ða1þa2þt

Þ&

þa2X

=ða1þa2þt

e ð

a2Y= a1

a22Y2

ð 1 dy y

ðy þ YÞ

Þ½

Þ&

ð 1 dz zm1 ðz þ ZÞm2 e ða1þa2þt

Þ½zþa2Z=ða1þa2þt

Þ&

þa2Z

=ða1þa2þt

N1N2

ð 1dt e a2ða1þt

ÞR

=ða1þa2þt

Þð 1dx xn1 ðx þ XÞn2 e ða1þa2þt

Þ½xþa2X=ða1þa2þt

Þ&

e ð

a2Y= a1

ð 1 dy y

ðy þ YÞ

Þ½

Þ&

ð 1 dz zm1 ðz þ ZÞm2 e ða1þa2þt

Þ½zþa2Z=ða1þa2þt

Þ&

N1N2

ð 1 dt e ½a2ða1þt

Þ=ða1þa2þt

Þ&R

dx x

a2X

a1 þ t2ÞX

n2 e

a1þa2þt2

a1 þ a2 þ t2

þ að1 þ a2 þ t2

ð 1

þ að1

t2 Y

ð 1

þ a2 þ t2

þ a2

þ t2

dy y

þ Þ

e a1

þa2

þt y

þ að1

t2 Z

ð Þ

ð 1

þ a2 þ t2

þ a2

þ t2

dz z

þ Þ

e a1þa2þt

The three integrals of the Cartesian coordinates have the same form. Take the integral with respect to x as, for example,

dx x

a2X

a1 þ t2ÞX

n2 e a1þa2þt2

ð 1

þ a2 þ t2

þ að1 þ a2 þ t2

n1!n2!

a2X n1 n1

ða1 þ t2ÞX n2 n2

X X

¼ n1 ¼ 0 n2 ¼ 0

n1!ðn1 n1Þ!n2!ðn2 n2Þ!

a1 þ a2 þ t2

ð 1 dx xn1þn2 e ða1þa2þt

Þx

ð96Þ

the crude born–oppenheimer adiabatic approximation

525

According to Eqs. (A.2) and (A.6), this integral is not zero only if n1 þ n2 is an even integer. That is,

dx x

a2X

a1 þ t2ÞX

n2 e

a1þa2þt2

þ a2 þ t2

þ að1 þ a2 þ t2

ð 1

n1 n1

a1 þ t2

n2 n2

n1!n2!Xn1þn2 ðn1þn2Þ

X X

¼ n1

¼ 0 n2 ¼ 0

n1!ðn1 n1Þ!n2!ðn2 n2Þ!

a1 þ a2 þ t2

þ ð

2n1þn2 ½ðn1 þ n2Þ=2&!ða1 þ a2 þ t2Þðn1þn2þ1Þ=2

ð Þ

n1þn2

ðn1 þ n2Þ!

Manipulating all three integrals in similar way, we have

1 hZ1jrjZ2i

¼ pN1N2

Xn1 Xn2 Xl1 Xl2 Xm1 Xm2 1 þ ð 1Þn1þn2

n1 ¼ 0 n2 ¼ 0 l1 ¼ 0 l2 ¼ 0 m1 ¼ 0 m2 ¼ 0

1 þ ð 1Þl1þl2 1 þ ð 1Þm1þm2!

Cn1 Cn2 Cl1 Cl2 Cm1 Cm2

ðn1 þn2Þ!ðl1 þl2Þ!ðm1 þ m2Þ!ð a2Þn1þl1þm1 n1 l1 m1

2n1 n2 l1

l2þm1þm2

n1þn2 ! l1þl2

m1þm2

m2þ m1þ m2þ 1

a22 a1 t2

=2a1 a2

t22 R2

ð 1 dt e½ ð

Þ ð þ þ

Þ&

n2þl2þm2 n2 l2 m2

½n1þn2þl1þl2þm1þm2 ðn1þn2þl1þl2þm1þm2Þ=2þ3=2&

þ a

where Cn

¼ n!=fðn nÞ!n!g. The remaining integral of t is

t2 =

t2 n2þl2þm2 n2 l2 m2

a1 þ

Þ ða1 þ a2

Þ&

e½ a2 a1þt

=ða1þa2þt

Þ&R

ð 1 ða½1ðþ a2 þ t2Þn1þl1þm1 ðn1 n2þl1 l2þm1 m2Þ=2þ3=2

t2 n2þl2þm2 n2 l2 m2

a1 þ

Þ ða1 þ a2

Þ&

e½ a2 a1þt

=ða1þa2

þt

Þ&R

ða½1ðþ a2 þ t2Þn1þl1þm1 ðn1 n2þl1 l2þm1 m2Þ=2þ3=2

ð0

ð99Þ

Introducing the new variable x

ð100Þ

x ¼ pa1 þ a2 þ t2

526	k. k. liang et al.

By considering the limits of integration, we ﬁnd that when t ¼ 0, x ¼ 0, and when t ¼ 1, x ¼ 1. Also,

a1 þ a2

101

ða1 þ a2 þ t2Þ3=2

dt ¼

ða1 þ a2 þ t2Þ3=2

ð102Þ

a1 þ a2

1 x2

103

a1 þ a2 þ t2

¼ a1 þ a2

a1 þ t2

a1 þ a2x2

104

a1 þ a2 þ t2 ¼

a1 þ a2

Therefore

I ¼ a1

=ða1

2 a2 0 dx e a2ða1þa2Þx2R2

þa2Þ aa1 1þ aa2x2

n1þl1þm1 ðn1 n2þl1 l2þm1 m2Þ=2

ð105Þ

Now, let

K1 ¼ n1 þ l1 þ m1 ðn1 n2 þ l1 l2 þ m1 m2Þ=2,

K2 ¼ n2 þ

l2 þ m2 n2 l2 m2. Notice that K2 is an integer, and K1 þ K2 ¼ n1 þ n2 þ l1 þ l2 þ m1 þ m2 ðn1 þ n2 þ l1 þ l2 þ m1 þ m2Þ=2 is also an integer, therefore K1 must be an integer. Thus,

2e a1a2R2= a1þa2Þ 1

2 2

I ¼

Þ2

Kð1

þK2þ1 ð0 dx e a2R =a1þa2x

1 x2

a1 þ a2x2

X X

2e a1a2R

=ða1þa2

K K

2 2

K1þK2þ1 k1

0 k2

0 Ck11 Ck22 ð 1Þ

1 a1

2 a22

ð0 dx x2ðk1þk2Þe a2R

=ða1þa2

ð106Þ

Again, making use of Eq. (A.16), we obtain

ð2k1 þ 2k2Þ!

dx x2ðk1þk2Þe a22R2x2=ða1

þa2Þ

ð0

! 4a22R2=

k1þk2

2 2

a1 þ a2Þp

erf

a2R

e a2R =ða1þa2Þ

2 k

k2 1

ð a2R

pa1

)

1 !

ð107Þ

the crude born–oppenheimer adiabatic approximation

527

By using the notation deﬁned in Eq. (A.13), we ﬁnd

X X

a2R2

2e a1a2R2

=ða1þa2

0 Ck11 Ck22 ð 1Þ

2 a22 Jk1þk2

ð108Þ

I ¼

K1þK2þ1 k1

0 k2

a1 þ a2

Further, deﬁning this integral as

;

t2ÞK2

e ½a2

þt2

=ða1þa2þt2Þ&R2

109

K1;K2 ð

a2Þ

ð 1

a2þ

K1þK2

we ﬁnd

jZ2i

hZ1j

X X X X X X

1Þn1þn2

1 þ ð 1Þl1þl2

¼ p

þ ð

0 l2

0 m1

1 m1þm2

þ ð Þ

Cn1

Cn2 Cl1 Cl2 Cm1

Cm2

ðn1 þ n2Þ!ðl1 þ l2Þ!ðm1 þ m2Þ!ð a2Þn1þl1þm1 n1 l1 m1

2n1

n1þn2 !

l1þl2

m1þm2

R; a1; a2

110

2 KK1;K2

m m

with K1 and K2 deﬁned as above.

In the case of hydrogen molecule, the term hZ1j1=jr þ R0j2jZ2i, which involves three centers, does not show up in the calculation. We will not discuss this integral in the present work.

D.Derivatives of the Coulomb Potential

In fact, the Coulomb integrals discussed in Section IV.C are available in contemporary quantum chemistry packages. We do not really need to develop our own method to calculate them. However, it is necessary to master the algebra so that we can calculate the matrix elements of the derivatives of the Coulomb potential. In the following, we shall demonstrate the evaluation of these matrix elements.

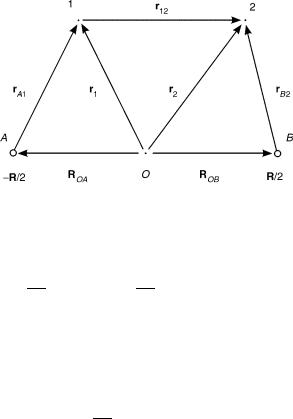
Since the derivative is taken with respect to the nuclear coordinate, it is important to choose the convenient coordinates. Earlier, we assigned the origin on one of the nuclei. Now, we will assign the origin on the middle point of the two nuclei. The geometry is shown in Figure 3. Furthermore, the z axis is taken to be along R. That is, the coordinates of the position of the nuclei A is

528	k. k. liang et al.

Figure 3. Molecular-ﬁxed coordinates.

RA ¼ ð0; 0; R=2Þ,

and

similarly

RB ¼ ð0; 0; R=2Þ.

Later,

calculate the

Coulomb interaction terms, we will be dealing with the following terms:

ð1 dt e t

rA1

ð1 dt e t

ðz1

þR=2Þ

ð111Þ

rA1

t2rB21

t2x12

t2y12

R=2

rB1

¼ pp ð1 dt e

ð112Þ

The quantities 1=rA2 and 1=rB2 are deﬁned similarly. In such cases, the ﬁrst derivatives are

ð1 dtð t2Þðzi þ R0=2Þe t

rAi

ð113Þ

rAi

t2rBi2

qR rBi

¼ pp ð1 dt t

ðzi R0=2Þe

ð114Þ

The second derivatives are

ð1

qqR2 rAi

¼ pp

dt"

þ t4

zi þ

#e t

rAi

ð115Þ

ð1

#e t

qqR2 rBi

¼ pp

þ t4

rBi

ð116Þ

dt"

Also, the notations of the wave functions are to be changed. We shall denote the Gaussian function centered at nucleus A as jZAi, and the function centered at nucleus B as jZBi.

the crude born–oppenheimer adiabatic approximation

529

hZAj qqR rA1 0jZAi

1. First-Order Derivatives

ð dt1 x1

ðz1 þ R0=2Þ

eð a1

¼ pp

ð 1 dtð t

2n 2 t2 x2

2 t2 y2

ð 1 dtð t Þ ð 1 dx1 x1 eð a1 Þ 1

ð 1 dy1 y1 eð a1 Þ 1

¼ pp

eð

2a1

ð117Þ

ð 1 dz1 zA1

Þ A1

Obviously, this matrix element is zero due to the integral over z. Similarly, we know that

hZBj qqR rB1

0jZBi ¼ 0

ð118Þ

hZAj qqR rA2

0jZAi ¼ 0

ð119Þ

hZBj qqR rB2

0jZBi ¼ 0

ð120Þ

Then, we consider

q 1

ð dt1 x1 y1 zA1 zB1e

2 2

ð121Þ

hZAj qR rB1

0jZAi ¼ pp

ð 1 dtð t

A1 e

t r

2n 2l 2m

By introducing a new variable for the z coordinate z ¼ zA1, since zB1 ¼ z R, we ﬁnd that

hZAj qqR rB1 0jZAi

e ð aAþ

¼ pp

ð 1 dtð t

Þ ð 1 dx1 x1 e ð aAþ

ð 1 dy1 y1

2 t

ðz

RÞe ð

2aA

2t2Rz

t2R2

ð122Þ

ð 1 dz z

530 k. k. liang et al.

According to Eqs. (A.2) and (A.6), the integral over x1 and y1 can be easily carried out, but the integral over z has to be manipulated.

Iz ¼ ð 1 dz z2mðz RÞe ð2aAþt

Þz

þ2t

Rz t

¼ e 2aAt

=ð2aAþt

ð 1 dz z2mðz RÞe ð2aAþt

Þ½z t

R=ð2aAþt

Þ&

¼ e 2aAt

=ð2aAþt

dz z þ 2aA

z 2aAaARt2

e ð2aAþt

Þz

ð 1

t2R

ð123Þ

We shall expand the polynomial of z. But recalling that only terms of the even power of z do not vanish, we can write the expansion in the following form:

e 2aAt2R2

2aAþt2

2aAR

C2m

t2R

2m 2m

dz z2me 2aAþt2

z ¼

ð 1

Þ(2aA

þ t2 m

2aA þ t2

t2R

2m 2mþ1

þ m

1 C22mm 1

ð 1 dz z2me ð2aAþt

Þz )

2aA þ t2

2aAR

t2R

e 2aAt2R2

2aAþt2

2aA

rþ

t2R

2m 2m

t2R

2aAR

þ m

1 C2m

2aA þ t2

2m 2m þ 1

2aA þ t2

ð 1 dz z2me ð2aAþt

Þz

ð124Þ

By inserting the expression for the integral over z, we ﬁnd

2aAp

=ð2aA

t2R

Iz ¼

t2 e 2aA t

þt

Þ( 2aAaR

2aA

rþ

2m 2m

C2m

t2R

2aAR

ð2mÞ!

þ m

2m 2m þ 1 2aA þ t2

2aA þ t2 22mm!

2aA þ t2

Þ(

e 2aA t2R2=

2aA

þt2

C2m ð2mÞ!

2aA

2m 22mm!

t2R

2m 2m

)

2aAR

ð125Þ

1 2aA

2aA

the crude born–oppenheimer adiabatic approximation

531

Thus, we obtain

hZAj qqR rB1 0jZAi

nþlþm 1þ3=2

t2R

N2 m

C2m

2n ! 2lÞ!ð2mÞ!

¼ p

A m 0

ð 4nÞþlðþmn!l!m!

ð 1

2aA þ t2

e 2aAt

=ð2aAþt

2aA þ t2

2m 2m þ 1

2aA þ t2

By introducing the new variable

x p

2aA þ t2

we have

2m 2mþ1

ð126Þ

ð127Þ

¼ x2

ð128Þ

2aA þ t2

1 x2

129

2aA þ t2 ¼

2aA

Therefore,

dt ¼ 2aA þ t2 3=2dx

ð130Þ

hZAj qqR rB1 0jZAi

nþlþm 1

2n ! 2l ! 2m

¼ 2pNA m 0

C2m

ð Þ ð Þ ð

mþ

4nþlþmn!l!m!

2aA

nþlþm 1

2m 2mþ1

2m þ 1

e 2aAR2x2

ð0

2m 2m þ 1

C2m

2nÞ!ð2lÞ!ð2mÞ!

nþlþ2m mþ1R2m 2mþ1

A m

4nþlþmn!l!m!

2aA

2aA ð0 dx 1 x2 nþlþm 1 2aAx2 2m 2mþ1e 2aAR2x2

2m þ 1

ð0

nþlþm 1

aAx

2m 2mþ2e 2aAR2x2

131

2m 2m þ 1

532

k. k. liang et al.

According to Eq. (106), let us deﬁne the integral

XK1;K2;a1;a2 ðRÞ ð0 dx 1 x2 K1 a1 þ a2x2 K2 e a22R2x2=ða1þa2Þ

X X

¼ k1

K K

dx x2ðk1þk2Þe a2R x =ða1þa2Þ

0 k2

0 Ck11 Ck22

ð 1Þ

1 a1 2

2 a22 ð0

X X

K k

K K

þk2

¼ k1

0 Ck11 Ck22

ð 1Þ

1 a1 2

2 a22 Jk1

ð132Þ

0 k2

With Eq. (131), letting a1 ¼ 0, a2 ¼ 2aA, we ﬁnd that

hZAj qqR rB1 0jZAi

nþlþ2m mþ1

2n ! 2l ! 2m !

¼ 2pNA m

0 C2m

ð Þ ð Þ ð Þ

mþ

4nþlþmn!l!m! 1

2aA

nþlþm 1;2m 2mþ1;0;2aA ð

2m þ 1

nþlþm 1;2m 2mþ2;0;2aA ð

Þ 2m 2m þ 1

ð133Þ

The matrix element between Gaussian functions at different centers is in general of the form

hZAj qqR rA1 0jZBi

NANB

ð134Þ

ð 1 dtð t2Þ

ð dt xAnA1xBnB1yAlA1yBlB1zAm1Aþ1zBm1B e aArA1

rA1

aBrB1

relations xA1 ¼ xB1 ¼ x1 x,

yA1 ¼ yB1 ¼ y1 y,

Since we can use

the

zA1 ¼ zB1 þ R, and let z zB1, we have

hZAj qqR rA1 0jZBi

NANB

ð 1 dtð t2Þ ð 1 dx xnAþnB e ðaAþaBþt

Þx

ð 1 dy ylAþlB e ðaAþaBþt

Þy

1 mB

aB t

ð 1 dz ðz þ RÞ þ z e ð

þ þ

ð þ

Þ ð

2nAþnBþlAþlB

the crude born–oppenheimer adiabatic approximation

533

NANB

ð 1 dtð t2Þe ðaAþt

ÞR

ð 1 dx xnAþnB e ðaAþaBþt

Þx

lA lB

aA aB

ð 1 dy y þ e ð

þ þ

ð1

dz ðz þ RÞmAþ1zmB e ðaAþaBþt2Þz2 2ðaAþt2ÞRz

	1				nAþnB			1ÞlAþlB	!
¼	NANB		1	1	nAþnB	1	þ ð	1ÞlAþlB
¼		pp		þ ð 2	Þ		þ ð	2

ðnA þ nBÞ!ðlA þ lBÞ!

nAþnB ! lAþlB !

2 2

ð 1 dt t2

e ðaAþt

ÞR

t2 aA

ðnAþnBþlAþlBÞ=2

ð1

dzðz þ RÞmAþ1zmB e ðaAþaBþt2Þ½zþðaAþt2Þ=ðaAþaBþt2Þ&

þðaAþt2Þ R2=ðaAþaBþt2Þ

	1				nAþnB			1ÞlAþlB	!
¼	NANB		1	1	nAþnB	1	þ ð	1ÞlAþlB
¼		pp		þ ð 2	Þ		þ ð	2

ðnA þ nBÞ!ðlA þ lBÞ!

nAþnB ! lAþlB !

2 2

ðnAþnBþlAþlBÞ=2

ð 1dt t2

e aBðaAþt

ÞR

=ðaA

þaBþt

mAþ1

þ m

dz z

aA þ t2

B e aAþaBþt2

ð 1

aA þ aB þ t2

þ aA þ aB þ t2

ð135Þ

Note that

dz z

R mAþ1

aA þ t2

mB e

aAþaBþt2

þ aA þ aB þ t2

ð 1

aA þ aB þ t2

mBþ1 mB

CmAþ1CmB

aBR

mA mAþ1 ðaA þ t2ÞR mB mB

X X

¼ mA

0 mB

aA þ aB þ t2

ð 1 dz zmAþmB e ðaAþaBþt

Þz

mA mAþ1 ðaA þ t2ÞR mB mB

mAþ1 mB

CmAþ1CmB

aBR

X X

¼ mA ¼ 0 mB ¼ 0

aA þ aB þ t2

þ ð

aA þ aB þ t2

rþ þ

A þ

ðmAþmBÞ=2

1 þ ð 1ÞmAþmB

ðmA

þ mBÞ!

aA aB

t2 2mA mB m

m =2 ! aA aB

ð136Þ

<<< < Предыдущая 36 37 38 39 40 41 42 43 44 45 46 4748 / 8248 49 50 51 52 53 54 55 56 57 58 59 60 > Следующая >>>

Соседние файлы в предмете Химия

#
15.08.20131.9 Mб22Antoniou I. - Advances in Chemical Physics, Volume 122, Dynamical Systems and Irreversibility (2002)(en).pdf
#
15.08.201311.33 Mб34Armarego W.L.F., Li Lin Chai C. - Purification of Laboratory Chemicals (2003)(5-th)(en).djvu
#
15.08.201317.3 Mб73Astruc D. - Modern arene chemistry (2002)(en).pdf
#
15.08.20131.25 Mб59auto_book.doc
#
15.08.20135.06 Mб120Baer M., Billing G.D. (eds.) - Advances in Chemical Physics. The Role of Degenerate States in Chemistry, Vol. 124 (2002)(en).pdf
#
15.08.20134.29 Mб17Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002).pdf
#
15.08.20137.08 Mб55Basov N.I. i dr. Raschet i konstruirovanie formiruyushchego instrumenta dlya izgotovleniya izdelij (1991.pdf
#
15.08.20135.59 Mб69Becker O.M., MacKerell A.D., Roux B., Watanabe M. (eds.) Computational biochemistry and biophysic.pdf
#
15.08.2013324.82 Кб32benzyne-cyclization.pdf
#
15.08.201314.48 Mб18Borowko M. 2000 Computational methods in surface and colloid science.djvu
#
15.08.20134.3 Mб49Brereton Chemometrics.pdf