
Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)
.pdf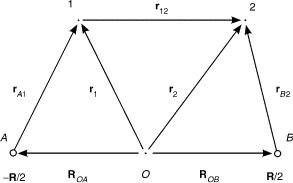



518 |
k. k. liang et al. |
B.The Overlap Integrals
Next, we consider the simple overlap integral of two such basis functions with different powers of Cartesian coordinates and different Gaussian width, centered at different points. Let nuclei 1 locate at the origin, and let nuclei 2 locate atR, then
Z1 |
i ¼ |
Nn1;l1;m1;a1 xn1 yl1 zm1 e a1ðx2þy2þz2 |
Þ |
|
|
|
|
|
ð |
73 |
Þ |
||||||||||||||
j |
|
|
|
|
|
|
n2 |
|
|
|
|
|
l2 |
|
|
|
|
|
m2 e a2½ðxþXÞ2 |
þðyþYÞ2þðzþZÞ2 |
& |
|
|||
Z2 |
i ¼ |
Nn2;l2;m2;a2 |
ð |
x |
þ |
X |
Þ |
ð |
y |
þ |
Y |
Þ |
ð |
z |
þ |
Z |
Þ |
ð |
74 |
Þ |
|||||
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
It can be observed that we can separate the overlap integral into the product of three independent spatial integrals
hZ1jZ2i ¼ Nn1;l1;m1;a1 Nn2;l2;m2;a2 IxIyIz |
|
|
|
ð75Þ |
|
1 |
2 |
|
|
2 |
|
Ix ¼ ð 1 dx xn1 ðx þ XÞn2 e a1x e a2 |
ðxþXÞ |
|
ð76Þ |
||
1 |
2 |
|
2 |
|
|
Iy ¼ ð 1 dy yl1 ðy þ YÞl2 e a1y e a2 |
ðyþYÞ |
|
ð77Þ |
||
1 |
2 |
|
2 |
|
|
Iz ¼ ð 1 dz zm1 ðz þ ZÞm2 e a1z e a2 |
ðzþZÞ |
|
ð78Þ |
||
Obviously, we do not need to calculate all three integrals. We shall calculate Ix and apply the formula to the other integrals.
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Ix ¼ ð 1 dx xn1 ðx þ XÞn2 e ða1þa2Þx |
2a2Xx a2X |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
||
¼ e a2X |
|
ð 1 dx xn1 ðx þ XÞn2 e ða1þa2Þ½xþa2X=ða1þa2Þ& þa2X |
=ða1þa2 |
Þ |
|
|||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
¼ e a1a2X |
=ða1 |
þa2Þ |
ð 1 dx xn1 ðx þ XÞn2 e ða1þa2Þx0 |
|
|
|
|
|
|
ð79Þ |
||||||||||||||||||||||
where x0 ¼ x þ a2X=ða1 þ a2Þ. Therefore x ¼ x0 |
a2X=ða1 þ a2Þ, and x þ X ¼ |
|||||||||||||||||||||||||||||||
x0 þ a1X=ða1 þ a2Þ. Thus, by changing the dummy variables, we have |
|
|
||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
1 |
|
|
|
|
2X |
|
|
|
n1 |
|
|
|
1X |
|
n2 |
|
|
2 |
|
|
||||||
Ix ¼ e a1a2X |
|
=ða1 |
þa2 |
Þ ð 1 dx x |
a |
|
|
x þ |
|
a |
|
|
e ða1þa2Þx |
|
|
|||||||||||||||||
|
a1 þ a2 |
|
a1 þ a2 |
|
|
|||||||||||||||||||||||||||
|
2 |
|
|
|
X X |
|
n ! |
|
|
|
|
n ! |
|
|
|
|
|
|
|
|
n1 n |
|
|
|
n2 m |
|||||||
|
|
|
|
|
n1 |
|
n2 |
|
|
|
|
|
|
|
|
|
a2 |
|
a1 |
|||||||||||||
¼ e a1a2X |
|
=ða1 |
þa2 |
Þ n |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||
|
0 m |
0 |
n1 |
n !n! |
n2 |
|
|
m |
!m! |
a1 a2 |
|
a1 a2 |
||||||||||||||||||||
|
|
|
|
|
|
¼ |
|
¼ |
|
ð |
Þ |
|
ð |
|
Þ |
|
|
|
|
þ |
|
|
|
|
|
þ |
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Xn1þn2 n m ð 1 dx xnþme ða1þa2Þx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ð80Þ |
||||||||||||||||

the crude born–oppenheimer adiabatic approximation |
519 |
According to the results shown in Appendix A, the integral in Eq. (80) is nonvanishing only when ðn þ mÞ is even. Consequently, Ix is a polynomial of order n1 þ n2 in X. If n1 þ n2 is even, Ix is an even polynomial; If n1 þ n2 is odd, Ix is an odd polynomial. Therefore, we can write the result as
|
rþ |
|
|
|
|
|||||||
|
|
|
p |
|
|
e |
a1a2 |
2 |
|
|
|
|
I |
x ¼ a1 |
|
|
|
a1þa2 |
X |
Xn1þn2 |
|
|
|||
|
|
a2 |
|
|
|
|
||||||
|
X X |
n1!n2!ðn þ mÞ! |
|
1 þ ð 1Þnþm |
|
|||||||
|
|
n1 |
n2 |
|
|
|
|
|||||
|
n 0 m |
¼ |
0 ðn1 nÞ!n!ðn2 mÞ!m!fn þ m=2g! |
2 |
|
|||||||
|
¼ |
|
|
|
|
|
|
|
|
|
||
|
½4ða1 þ a2Þ& ðnþmÞ=2X n m |
ð81Þ |
||||||||||
Iy and Iz are obtained in exactly the same way.
C.Interaction Terms with the Nuclei
Next, we shall consider four kinds of integrals. The first is the expectation value of the Coulomb potential by one nucleus for one of the primitive basis function centered at that nucleus. The second is the expectation value of the Coulomb potential by one nucleus for one of the primitive basis function centered at a different point (usually another nucleus). Then, we will consider the matrix element of a Coulomb term between two primitive basis functions at different centers. The third case is when one basis function is centered at the nucleus considered. The fourth case is when both basis functions are not centered at that nucleus. By that we mean, for two Gaussian basis functions defined in Eqs. (73) and (74), we are calculating
|
|
|
1 |
|
N2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
|
|
|
|
|
||||
|
|
hZ1j |
|
jZ1i ¼ p1p |
ð 1 dt |
ð dt x2n1 y2l1 z2m1 e 2a1r e t |
r |
|
|
|
|
|
|
|||||||||||||||||
|
|
r |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 |
|
N2 |
1 |
|
|
|
|
|
|
|
|
2n |
|
|
2l |
|
|
|
2m |
2 |
2 |
|
2 |
||||
|
|
hZ2j |
|
jZ2i ¼ p2p |
ð 1 dt |
ð dt ðx þ XÞ |
|
1 ðy þ YÞ |
1 ðz þ ZÞ |
|
1 e 2a2jrþRj |
e t |
r |
|
||||||||||||||||
|
|
r |
|
|
|
|
||||||||||||||||||||||||
|
|
|
1 |
N1N2 |
1 |
|
|
|
|
|
n1 |
|
|
|
n2 l1 |
|
|
|
l2 m1 |
m2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
a2 |
|
r |
R |
|
t2r2 |
|
|
|
|
þ YÞ z ðz þ ZÞ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
a1r2 |
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
hZ1jrjZ2i ¼ pp |
ð 1 dt |
ð dt x |
|
ðx þ XÞ y ðy |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
e |
e |
|
|
j þ |
|
j e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
N1N2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
hZ1j |
|
|
|
|
jZ2i ¼ |
|
pp |
ð 1 dt ð dt xn1 ðx þ XÞn2 yl1 ðy þ YÞl2 zm1 ðz þ ZÞm2 |
|
|
|
|||||||||||||||||||
r |
þ |
R0 |
|
|
|
|
|
|||||||||||||||||||||||
j |
|
|
j |
|
a1r2 |
a2 |
|
r |
R |
2 |
t2 r |
R0 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
e |
e |
|
|
j þ |
|
j e |
|
j þ |
|
j |
|
|
|
|
|
|
|
|
|
|
|||

|
|
the crude born–oppenheimer adiabatic approximation |
|
|
521 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Consider the integral |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I2 ¼ ð 1 dt |
ð 1 dx x2ne 2ax |
|
e t |
ðx |
2XxþX |
|
|
Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
ð 1 dy y2le 2ay |
e t |
ðy |
|
2YyþY |
|
Þ |
|
ð 1 dz z2me 2az |
e t |
|
ðz |
2ZzþZ |
|
Þ |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
2 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
¼ ð 1 dt e t |
R |
|
ð 1 dx x2ne ð2aþt |
|
Þx |
|
þ2t |
|
Xx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ð 1 dy y2le ð2aþt |
|
Þy |
þ2t |
|
Yy ð 1 dz z2me ð2aþt |
Þz |
þ2t |
Zz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
2 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
¼ ð 1 dt e t |
R |
|
ð 1 dx x2ne ð2aþt |
|
Þ½x t |
|
X=ð2aþt |
|
Þ& |
et |
|
X |
|
=ð2aþt |
|
|
Þ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
4 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ð 1 dy y2le ð2aþt |
|
Þ½y t |
|
Y |
=ð2aþt |
Þ& |
|
et |
|
Y |
|
=ð2aþt |
|
Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
4 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ð 1 dz z2me ð2aþt |
|
Þ½z t |
|
|
Z=ð2aþt |
|
Þ& |
et |
|
Z |
|
=ð2aþt |
|
Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2X |
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
¼ ð 1 dt e 2at |
|
=ð2aþt |
ÞR |
|
|
ð 1 dx x þ |
|
|
|
|
|
|
|
e ð2aþt |
Þx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2a þ t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
t2Y |
|
|
|
|
|
|
2l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2Z |
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|||||||||||||||||
ð 1 dy y þ |
|
|
|
|
|
|
|
|
|
e ð2aþt |
|
Þy |
|
|
ð 1 dz |
z þ |
|
|
|
|
e ð2aþt |
Þz |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2a þ t2 |
|
|
|
|
|
|
2a þ t2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
2 |
2 |
|
|
|
|
2 |
|
|
" |
|
2n |
|
|
|
|
|
|
|
|
2n ! |
|
|
|
|
|
|
|
|
t2X |
|
|
|
|
2n n 1 |
|
|
|
|
|
2 |
|
2 |
|
|
|||||||||||||||||||||||||||||
¼ |
|
dt e 2at |
|
R |
=ð2aþt |
|
|
Þ |
|
|
|
|
|
|
|
|
|
2nð |
|
|
|
|
Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xne 2aþt |
|
x dx |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n !n! 2a |
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
ð 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n¼ |
|
|
ð |
|
|
|
|
Þ |
|
|
|
|
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
ð 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
" |
2l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
2l l 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2l ! |
|
|
|
|
|
|
|
t2Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
ð |
|
Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yle |
|
|
2aþt |
|
Þ |
y dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2l |
|
l !l! 2a |
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
l¼0 |
ð |
|
Þ |
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
|
ð 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
" |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2m |
|
|
|
2m ! |
|
|
|
|
|
|
|
|
|
t2Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
ð |
|
|
Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zme |
ð |
2aþt |
|
Þ |
z |
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
2m |
|
|
m !m! 2a |
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
m¼ |
|
ð |
|
|
Þ |
|
|
|
|
|
|
|
|
þ |
|
|
ð 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 2n |
1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2X |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
||||||||||||||||||
¼ |
dt e 2at |
|
R |
=ð2aþt |
|
|
Þ |
" |
|
|
|
|
|
|
|
|
|
|
|
ð |
Þ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2ne ð2aþt |
Þx dx# |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
0 |
|
|
2n |
|
|
|
|
2n ! 2n ! |
2a t2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
ð 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¼ |
|
|
ð |
|
|
|
|
|
|
|
|
Þ ð |
|
|
|
Þ |
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
ð 1 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
t2Y |
|
|
|
|
|
|
|
2l 2l |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
" |
|
|
|
|
|
|
ð Þ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2le ð2aþt |
|
Þy |
dy# |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
l¼0 |
ð |
|
Þ ð Þ |
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
ð 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m 2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
m |
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Z |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
" |
|
|
|
|
|
ð2 Þ! |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
z2me ð2aþt |
|
|
Þz |
dz# |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
m¼ |
0 |
ð |
2m |
|
2m ! 2m ! |
2a |
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Þ ð Þ |
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
|
|
ð 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
ð1 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
¼dt e 2at2R2=ð2aþt2Þ
1


