
Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)
.pdf676 a. j. c. varandas and z. r. xu
requirement in low-energy spectroscopic studies. We should note though that, if their interchange becomes feasible by increasing the energy, the potential energy surface must satisfy the full permutational symmetry requirement dictated by the physical identity alone; this is typically the case in reaction dynamics studies. Another example is the molecule H12C 13CH where two hydrogen atoms have nonequivalent chemical environments. Again, although the two hydrogen atoms may be distinguishable from the spectroscopic point of view, the corresponding full potential energy surface must generally be symmetric with respect to their permutation; note that in the BO approximation, the potential energy surface does not depend on the mass of the nuclei, and hence it is the same as for H12C 12CH. In summary, the permutational symmetry requirement should be applied only to identical particles that are both physically and chemically indistinguishable. In this case, chemical identity implies physically identical particles that have equivalent environments in the molecule and can be brought about by proper rotations of the nuclear framework, or else physically identical particles that may have equivalent chemical environments through some feasible dynamical process. Thus, the concept of chemical identity depends on the energy regime under consideration. Ideally, one should therefore carry out the nuclear dynamics studies using a global potential energy surface [57,58], which has built-in the full permutational symmetry implied by the physical identity of the atoms. Of course, if the equivalent minima are separated from each other by high energy barriers, then it may be an excellent approximation to have just the representation for one of the equivalent minima if one assumes that underbarrier tunneling is negligible. In other words, the concept of chemical identity delimits the nuclei motion to a part of the molecule configuration space. Hereafter, we will refer to identical particles with the above understanding.
Let us examine a special but more practical case where the total molecular
^ |
^ |
Þ, as is the |
Hamiltonian, H, can be separated to an electronic part, Heðr; s; R0 |
||
case in the usual BO approximation. Consequently, the total molecular wave function ðR0; i; r; sÞ is given by the product of a nuclear wave function
wnucðR0; iÞ and an electronic wave function ceðr; s; R0Þ. We may then talk separately about the permutational properties of the subsystem consisting of
electrons, and the subsystem(s) formed of identical nuclei. Thus, the following
commutative laws |
^ |
^ |
¼ 0 and |
|
^ |
^ |
¼ 0 must be satisfied; X ¼ |
|
Pe; He |
PX; HN |
|||||||
A; B; . . . , and all |
|
|
|
|
|
|
|
|
|
other symbols have their usual meaning. |
|||||||
As pointed out in the previous paragraph, the total wave function of a molecule consists of an electronic and a nuclear parts. The electrons have a different intrinsic nature from nuclei, and hence can be treated separately when one considers the issue of permutational symmetry. First, let us consider the case of electrons. These are fermions with spin 12, and hence the subsystem of electrons obeys the Fermi–Dirac statistics: the total electronic wave function

permutational symmetry and the role of nuclear spin |
677 |
must be antisymmetric under permutation of any two electrons. This requirement implies the Pauli exclusion principle, which states that two electrons cannot occupy the same spin orbital.
Commonly, nuclear dynamics treatment in molecules neglect the interactions between the nuclear spin and the other nuclear and electronic degrees of freedom in the system Hamiltonian. As a result, the eigenenergies become independent of the nuclear spin. In this case, one must impose the requirements that the symmetry properties of the nuclear spin on the total wave function are satisfied, since the nuclei in the molecule have their specific statistical properties. As it is well known, nuclei having zero or integer nuclear spin quantum numbers are bosons and must obey the Bose–Einstein statistics: The nuclear wave function must therefore be symmetric under permutation of any two identical bosonic particles. On the other hand, nuclei having half-integer spin quantum numbers are fermions and must obey the Fermi–Dirac statistics: The nuclear wave function must in this case be antisymmetric with respect to the permutation of any two fermionic nuclei. For example, 7Li is a fermion with nuclear spin 32, and 6Li is a boson with nuclear spin 1. Thus, the total wave function of 7Li3 must be antisymmetric under the permutation of the three identical nuclei (note that this involves a three-pair change); see the corresponding S3 permutational group in Table III. Conversely, the total wave function of 6Li3 must be symmetric under the permutation of the three identical nuclei. In turn, the total wave function of 7Li2 6Li must be antisymmetric under the permutation S2 of the two identical 7Li nuclei (see also Table III for the S2 permutational group). Following the same reasoning, the total wave function of 6Li2 7Li must be symmetric under the permutation of the two identical 6Li nuclei.
Let us discuss further the permutational symmetry properties of the nuclei subsystem. Since the electronic spatial wave function ceðr; s; R0Þ depends parametrically on the nuclear coordinates, and the electronic spacial and spin coordinates are defined in the BF, it follows that one must take into account the effects of the nuclei under the permutations of the identical nuclei. Of course,
TABLE III
Species and Characters of the S2 and S3 Permutational Groups
S2 |
|
(1) |
(12) |
[2] |
|
1 |
1 |
½12& |
|
1 |
1 |
S3 |
ð1Þ |
2ð123Þ |
3ð12Þ |
½33& |
1 |
1 |
1 |
½1 & |
1 |
1 |
1 |
½21& |
2 |
1 |
0 |
678 |
a. j. c. varandas and z. r. xu |
the spin part of the electronic wave function is independent of the permutational properties of the nuclei, which implies that one does not need to take care of the electronic spin wave function when dealing with the permutational properties of the nuclei. However, as it is will be further discussed in Section VIII, the electronic spin S will influence the permutational symmetry properties through the total angular momentum J. Accordingly, we address in the following sections the consequences of such rules based on the premise that the total wave function ðR0; i; r; sÞ may be written as
ðR0; i; r; sÞ ¼ ceðr; s; R0ÞwvðRÞwrðR^ÞwnsðiÞ |
ð47Þ |
^ |
wnsðiÞ are the electronic, vibrational, |
where ceðr; s; R0Þ, wvðRÞ, wrðRÞ, and |
rotational, and nuclear spin functions, respectively.
V.PERMUTATIONAL SYMMETRY OF NUCLEAR
SPIN FUNCTION
As discussed before, the nuclear spin functions must belong to one of the irreducible representations of the double group of the molecule. For example, 6Li3 may have nuclear spin quantum numbers I ¼ 0, 1, 2, and 3, and hence the
permutational symmetries under S3 will be given according to Table II: A01 for I ¼ 0; A02 þ E00 for I ¼ 1; A01 þ E0 þ E00 for I ¼ 2, and so on. For a molecule
with half-integer nuclear spin, all the IRREPs are double-valued due to the Kramers’ degeneracy. For example, for 7Li3, the nuclear spin quantum numbers I are half-integer ranging in steps of 1 from 12 up to 92. Thus, from Table II, the permutation symmetries under S3 will be E1=2 for I ¼ 12; E1=2 þ E3=2 for I ¼ 32;
E1=2 þ E3=2 þ E5=2 for I ¼ 52, and so on.
For a nucleus with spin quantum number I ¼6 0, there are ð2I þ 1Þ values of
the z component mI of the spin nuclear |
angular momentum, |
with mI ¼ |
||||||||
I; I þ 1; . . . ; I 1; I.2 For two such nuclei, the total number of mI |
combi- |
|||||||||
nations will be ð2I þ 1Þ . Assuming that wmI ð1Þ is the nuclear spin function of |
||||||||||
nucleus 1 with quantum number m |
|
2I |
þ 1Þ |
|
functions of the |
|||||
|
|
I, there are ð |
|
spin |
|
2 |
ð2I þ 1Þ |
|||
form wmI ð1ÞwmI ð2Þ, which are symmetric. Of the remaining ð2I þ 1Þ |
|
|||||||||
ones, one-half can be combined in symmetric states |
|
|
|
|
|
|||||
1 |
|
ð1ÞwmI ð2Þi |
mI ¼6 mI0 |
ð48Þ |
||||||
wnsS ð1; 2Þ ¼ p2 hwmI ð1ÞwmI0 ð2Þ þ wmI0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
and the other one-half in antisymmetric ones |
|
|
|
|
|
|
|
|
||
1 |
|
ð1ÞwmI ð2Þi |
mI 6¼ mI0 |
ð49Þ |
||||||
wnsA ð1; 2Þ ¼ p2 hwmI ð1ÞwmI0 ð2Þ wmI0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|

permutational symmetry and the role of nuclear spin |
679 |
||||
The total number of symmetric states is then |
|
||||
1 |
½ð2I þ 1Þ2 ð2I þ 1Þ& ¼ ð2I þ 1ÞðI þ 1Þ |
ð50Þ |
|||
2I þ 1 þ |
|
||||
2 |
|||||
and the total number of antisymmetric states is |
|
||||
1 |
½ð2I þ 1Þ2 ð2I þ 1Þ& ¼ ð2I þ 1ÞI |
ð51Þ |
|||
|
|
||||
|
2 |
||||
In summary, for a homonuclear diatomic molecule there are generally ð2I þ 1Þ ðI þ 1Þ symmetric and ð2I þ 1ÞI antisymmetric nuclear spin functions. For example, from Eqs. (50) and (51), the statistical weights of the symmetric and antisymmetric nuclear spin functions of 7Li2 will be 58 and 38, respectively. This is also true when one considers 7Li2 6Li and 6Li2 7Li. For the former, the statistical
weights of the symmetric and antisymmetric nuclear spin functions are |
5 and 3, |
||||||||||
respectively; for the latter, they are 2 |
and 1 |
in the same order. |
|
8 |
|
8 |
|||||
|
|
|
|
|
|||||||
|
|
3 |
3 |
|
|
|
ð2I þ 1Þ |
||||
ð |
For a homonuclear triatomic molecule |
there |
are |
similarly [29] |
|||||||
2I |
þ 3ÞðI þ 1Þ=3 symmetric, ð2I þ 1Þð2I 1ÞI=3 |
7 |
|
ð |
2I |
þ |
1 |
Þ |
|||
|
|
|
|
antisymmetric, and |
|
|
|
||||
ðI þ 1Þð8IÞ=3 degenerate nuclear spin functions. For |
Li3, one therefore has 20 |
||||||||||
symmetric, 4 antisymmetric, and 40 degenerate nuclear spin functions. The corresponding statistical weights will then be 165 , 161 , and 1016. Following a similar reasoning for 6Li3 one finds 10 symmetric, 1 antisymmetric, and 16 degenerate
nuclear spin functions. Thus, the corresponding statistical weights are |
10, |
|
1 |
, |
||||
27 |
||||||||
and 16. |
|
|
27 |
|
||||
|
|
|
|
|
|
|||
|
27 |
|
|
|
|
|
|
|
|
Now, consider a linear polyatomic |
molecule. If this is of the |
type |
|||||
Z |
BAAB |
^ |
rotation about an axis perpendicular |
|||||
Z with D1h geometry, a C2 |
||||||||
to the molecular axis at its midpoint will exchange pairs of identical nuclei. If
^ |
rotation leads |
the nuclei A; B; . . . ; Z contain an odd number of fermions, the C2 |
to a change of sign of the total wave function; otherwise, it will remain unchanged. By repeated application of the two identical nuclei case, the total
|
of possible nuclear spin wave functions will be given by |
ð |
2I |
2 |
||||||
number |
A þ 1Þ |
|||||||||
|
2 |
ð2IZ þ 1Þ |
2 |
|
|
|
||||
ð2IB þ 1Þ |
|
|
, where IX |
denotes the nuclear spin of |
X |
ðX ¼ A; |
||||
B; . . . ; ZÞ. Similarly, the number of possible symmetric and antisymmetric nuclear spin functions can be obtained by an extension of the method used for diatomic molecules. The total number of symmetric states is then given by [56]
ð2IA þ 1Þð2IB þ 1Þ ð2IZ þ 1Þ½ð2IA þ 1Þð2IB þ 1Þ ð2IZ þ 1Þ þ 1&=2
ð52Þ
and the total number of antisymmetric states is [56]
ð2IA þ 1Þð2IB þ 1Þ ð2IZ þ 1Þ½ð2IA þ 1Þð2IB þ 1Þ ð2IZ þ 1Þ 1&=2
ð53Þ
680 |
a. j. c. varandas and z. r. xu |
which represent the corresponding nuclear statistical weights. For molecules of the form Z BARAB Z with D1h symmetry, the corresponding numbers must each be multiplied by [56] ð2IR þ 1Þ.
VI. PERMUTATIONAL SYMMETRY OF ELECTRONIC
WAVE FUNCTION
In considering the nuclear permutational properties of the total wave function, we must have in mind the corresponding properties of the electronic wave function, since this depends parametrically on the nuclear geometry. The permutational properties of ceðr; s; R0Þ under identical-nuclei exchange are
^ |
Þ, and hence of VnðRÞ. Since this represents |
determined by those of Heðr; s; R0 |
the potential energy of the electrons in the field of the fixed nuclei, it must have the symmetry of the molecule in its nth electronic state. The electronic eigenfunctions for nondegenerate states can therefore only be symmetric or antisymmetric with respect to each symmetry operation that is allowed by the symmetry of the molecule in its equilibrium geometry. For degenerate states, a symmetry operation can only transform an eigenfunction into a linear combination of the degenerate eigenfunctions such that the electron density remains unaltered.
Let us begin by considering a homonuclear diatomic molecule. Clearly, permutation of the nuclei does not affect the internuclear distance, but it does affect the electronic spatial coordinates, since they are defined with respect to the BF axes. To find the effect of interchanging nuclei on the electronic wave function, we invert first the SF coordinates of the nuclei and electrons, and then carry out a second inversion of the SF electronic coordinates alone. The net effect will be the exchange of the SF coordinates of the two nuclei as illustrated in Figure 2. Note that the inversion of the SF does not affect electronic and nuclear spin coordinates. The eigenvalues ( 1) of such an inversion operator indicate the parities of the wave function under consideration. The first inversion (equivalent to a reflection s^v) leaves the electronic wave functions unchanged (i.e., with even parity) for þ; þ; . . . electronic states, while it changes their sign (i.e., with odd parity) for ; ; . . . electronic states. This is due to the fact that reflection in the plane containing the nuclei changes (leaves unchanged) the sign of wave function for (þ) states. Because only the þ andhave different energies [56], it has often omitted the sign for degenerate states such as ; . . . provided that -type doubling is ignored. The second of the above inversion operations (which inverts back the electronic SF coordinates), inverts the electronic BF coordinates since the nuclei are unaffected by this step, and hence the electronic wave functions can be classified as g or u states according to whether such inversion of the electronic BF coordinates changes or leaves unchanged the sign of the electronic wave function. Thus,
permutational symmetry and the role of nuclear spin |
681 |
||
gþ; u ; gþ; u |
electronic states have wave functions that are symmetric |
||
under permutation of identical nuclei, whereas g ; uþ; g ; uþ |
electronic |
||
states are antisymmetric under such a permutation. The permutational symmetry for linear polyatomics D1h follows similar arguments.
We now consider planar molecules. The electronic wave function is expressed with respect to molecule-fixed axes, which we can take to be the abc principal axes of inertia, namely, by taking the coordinates ðx; y; zÞ in Figure 1 coincided with the principal axes ða; b; cÞ. In order to determine the parity of the molecule through inversions in SF, we first rotate all the electrons and nuclei by 180 about the c axis (which is perpendicular to the molecular plane); and then reflect all the electrons in the molecular ab plane. The net effect is the inversion of all particles in SF. The first step has no effect on both the electronic and nuclear molecule-fixed coordinates, and has no effect on the electronic wave functions. The second step is a reflection of electronic spatial coordinates in the molecular plane. Note that such a plane is a symmetry plane and the eigenvalues of the corresponding operator s^v then determine the parity of the electronic wave function.
In order to determine the permutational symmetry of a nonlinear molecule, one can invoke the permutation group. Here, we give some examples. As is known, the permutation group S3 is isomorphic to the point group C3v, and ½13& irreducible representation in the S3 is antisymmetric with the interchange (12) of any two indentical particles (see Tables I and III). Thus, the A2 electronic state for a molecule of C3v geometry must be antisymmetric with such interchange of the indentical nuclei. It is obvious that the totally symmetric IRREPs in point groups always correspond to the ½n& IRREPs in groups Sn.
Let us focus on the electronic wave function of ground state Li3, which is known to have B2 symmetry at its equilibrium geometry in the C2v point group. In order to determine the permutation symmetry of the B2 electronic state under the interchange of identical nuclei, we notice a correlation between IRREPs of the group C2v and those of the group C2 (see Tables I and III). It is found that B2 IRREP in the group C2v is correlated with the B IRREP in the group C2. In addition, we know that the group C2 is isomorphic to the permutation group S2, and the B IRREP in C2 corresponds to the antisymmetric IRREP ½12& in S2. Accordingly, the B2 electronic state must be antisymmetric with the interchange of the two identical nuclei. In fact, in the B2 IRREP of C2v, the wave function
^
changes sign under a C2 operation. In contrast, the electronic wave function at the lowest point of the conical intersection on the upper sheet of the Li3 potential energy surface has degenerate character under S3, since this geometry transforms as E0 in the D3h symmetry point group. Next, consider the isotopomer 7Li2 6Li. With the substitution of 7Li by the isotope 6Li, the permutational symmetry group of the system has been reduced from S3 to S2. Thus, if existing, the spatial degeneracy upon permutation of the nuclei can be

682 |
a. j. c. varandas and z. r. xu |
|
TABLE IV |
Resolution of Species of Symmetric Point Groups into Some Point Groups of Lower Symmetry
Kh |
D3h |
C3v |
C2v |
|
Cs |
|
Dg0 Sg |
A10 |
|
A1 |
A1 |
|
A0 |
Du0 Su |
A100 |
|
A2 |
A2 |
|
A00 |
Dg1 Pg |
A20 þ E00 |
A2 þ E |
A2 þ B1 þ B2 |
A0 þ 2A00 |
||
Du1 Pu |
A200 þ E0 |
A1 þ E |
A1 þ B1 þ B2 |
2A0 þ A00 |
||
Dg2 Dg |
A10 þ E0 |
þ E00 |
A1 þ 2E |
2A1 þ A2 þ B1 þ B2 |
3A0 |
þ 2A00 |
Du2 Du |
A100 þ E0 |
þ E00 |
A2 þ 2E |
A1 þ 2A2 þ B1 þ B2 |
2A0 |
þ 3A00 |
removed in part or completely, since F is an integer. This is indeed the case for the ground state of 7Li2 6Li, with the electronic wave function at the minimum of the lower sheet of the potential energy surface being antisymmetric under S2. Similarly, the electronic wave function at the lowest point of the conical intersection on the upper sheet of the 7Li2 6Li potential energy surface will be symmetric or antisymmetric4 under S2. The spatial degeneracy of the electronic wave function has therefore been removed when resolving D3h into C2v, since the E0 state of the lowest energy structure has been resolved into A1 B2 (see Table IV, where the same axis convention as in [28] has been followed: the highest order proper axis always coincides with the z axis.) which correspond to symmetric and antisymmetric wave functions in S2.
VII. PERMUTATIONAL SYMMETRY OF ROVIBRONIC AND
VIBRONIC WAVE FUNCTIONS
Since the total wave function must have the correct symmetry under the permutation of identical nuclei, we can determine the symmetry of the rovibronic wave function from consideration of the corresponding symmetry of the nuclear spin function. We begin by looking at the case of a fermionic system for which the total wave function must be antisymmetric under permutation of any two identical particles. If the nuclear spin function is symmetric then the rovibronic wave function must be antisymmetric; conversely, if the nuclear spin function is antisymmetric, the rovibronic wave function must be symmetric under permutation of any two fermions. Similar considerations apply to bosonic systems: The rovibronic wave function must be symmetric when the nuclear spin function is symmetric, and the rovibronic wave function must be antisymmetric when the nuclear spin function is antisymmetric. This warrants
4 This and the previous statements can be understood from Tables IX and X, which will be discussed in more detail in subsequent sections.
permutational symmetry and the role of nuclear spin |
683 |
that the total wave function is totally symmetric under permutation of any two indistinguishable bosons.
As was shown in the preceding discussion (see also Sections VIII and IX), the rovibronic wave functions for a homonuclear diatomic molecule under the permutation of identical nuclei are symmetric for even J rotational quantum numbers in þg and u electronic states; antisymmetric for odd J values in þg and u electronic states; symmetric for odd J values in g and þu electronic states; and antisymmetric for even J values in g and þu electronic states. Note that the vibrational ground state is symmetric under permutation of the two nuclei. The most restrictive result arises therefore when the nuclear spin quantum number of the individual nuclei is 0. In this case, the nuclear spin function is always symmetric with respect to interchange of the identical nuclei, and hence only totally symmetric rovibronic states are allowed since the total wave function must be symmetric for bosonic systems. For example, the 12C nucleus has zero nuclear spin, and hence the rotational levels with odd values of J do not exist for the ground electronic state (1 þg ) of 12C2.
Let us now examine the features of the nuclear probability density of a X3 molecule (X is an 2S atom) in its electronic groundand first-excited doublet states. For the lowest vibronic A1 states, such a nuclear probability density must clearly concentrate5 at the regions where the potential energy surface itself has A1 symmetry, which correspond in the case of homonuclear trimeric 2S systems to the saddle points of the potential energy surface having 2A1 symmetry in C2v. Instead, the nuclear probability density of the lowest A2 vibronic states will concentrate at regions where the potential energy surface has A2 symmetry; note that the potential energy surface at the minima has 2B2 symmetry in C2v, and hence A2 in S3. Both the A1 and A2 probability densities display threefold symmetries on a relaxed triangular plot such as that employed in Figure 3 to represent the Li3 potential energy surface. Although the nuclear probability density of each component for the E vibronic state has twofold symmetry, their sum must also have threefold symmetry.
VIII. PERMUTATIONAL SYMMETRY OF ROTATIONAL
WAVE FUNCTION
The permutational symmetry of the rotational wave function is determined by the rotational angular momentum J, which is the resultant of the electronic spin S, electronic orbital L, and nuclear orbital N angular momenta. We will now examine the permutational symmetry of the rotational wave functions. Two important remarks should first be made. The first refers to the J ¼ 0 rotational
5 Of course, for highly excited states, the density is expected to cover wide portions of the molecular configuration space.
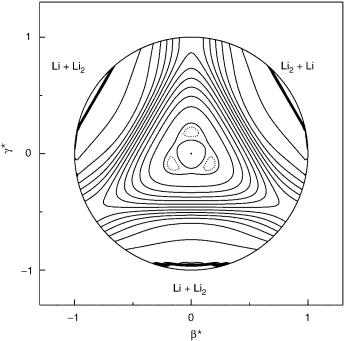
684 |
a. j. c. varandas and z. r. xu |
Figure 3. Relaxed triangular plot [68] of the Li3 ground-state potential energy surface using hyperspherical coordinates. Contours, are given by the expression EnðeVÞ ¼ 0:56 þ 0:045ðn 1Þ with n ¼ 1; 2; . . . , where the dashed line indicates the level 0:565 eV. The dissociation limit indicated by the dense contouring implies Li2ðX1 þg Þ þ Li.
state, which must be totally symmetric. The second emerges from the extended Kramers’ theorem, which imposes half-integer J rotational states to be degenerate. Thus, the lowest rotational state for the electronic ground state of Li3 corresponds to J ¼ 12, and must be degenerate.
Next, we address some simple cases, begining with homonuclear diatomic molecules in 1 electronic states. The rotational wave functions are in this case
w ð^Þ
the well-known spherical harmonics: for even J values, r R is symmetric
w ð^Þ
under permutation of the identical nuclei; for odd J values, r R is antisymmetric under the same permutation. A similar statement applies for any D1h type molecule.
When the molecule is not in a 1 state there is an interaction between the rotation of the molecule and S and/or L, and the details of coupling the angular momenta are involved. Most nonsinglet molecules with electronic orbital angular momentum ¼ 0 obey Hund’s case (b) coupling. In Case (b), the electronic orbital angular momentum combines with the nuclear orbital angular
permutational symmetry and the role of nuclear spin |
685 |
momentum to give a total angular momentum associated with the quantum
number N ¼ ; þ 1; þ 2; . . . . Note that |
in |
this case, N is the proper |
rotational angular momentum. Accordingly, |
for |
^ |
even N values, wrðRÞ is |
w ð^Þ symmetric under permutation of the identical nuclei; for odd N values, r R is
antisymmetric under the same permutation. Thus, since the N ¼ 0; 2; 4; . . .
rotational levels for the 3 g electronic state of 16O2 are symmetric with respect to the interchange two 16O nuclei, they cannot exist according to the Pauli principle (see later). For most molecules with electronic orbital angular momentum > 0 one has Hund’s case (a). In Case (a), the axial components of electronic orbital angular momentum combine with the electronic spin angular momentum to give a resultant axial component of total electronic angular momentum associated with the quantum number ¼ j þ j. The resultant angular momentum then combines with the nuclear orbital angular momentum to give a total angular momentum (exclusive of nuclear spin) J, where J ¼ ; þ 1; þ 2; . . . . If J is a half-integer, the rotational levels will be doubly degenerate in the zeroth-order approximation. Yet, the interaction between electronic and rotational motions can lead to the splitting of the degenerate electronic level into the nondegenerate þ and electronic states (so-called -type doubling).
Now, we consider the case of a planar molecule. In general, the rotational wave functions depend on the Eulerian angles ða; b; gÞ. For planar symmetric tops, the angles a and b give the orientation of the positive direction of the molecular symmetry axis with respect to SF coordinates, while g is the angle of rotation about the symmetry axis. The angles a and b are unchanged by inversion, while g is increased by p. The angle g enters the symmetric top wave function as the factor expðiKgÞ, where the quantum number K is the component of the rotational angular momentum J along the molecule-fixed axis. Thus, the inversion multiplies the rotational wave function by expðiKpÞ ¼ ð 1ÞK and its parity will be even for even K and odd for odd K. For planar asymmetric tops, the symmetric top wave functions that occur in the expansion of a given asymmetric top wave function all have either even values of K or odd values of K. A planar symmetric top must be an oblate top. If the asymmetric top level correlates with an oblate top level with K even, then it must be a linear combination of oblate top functions with even K values; similarly for the K-odd correlation. Thus, parities of the asymmetric top wave functions are determined by the values of K. Consider now a homonuclear triatomic molecule, where K is the quantum number for the rotational angular momentum component perpendicular to the plane defined by the three atoms. The rotational contribution to the permutational symmetry [59] is then symmetric if K ¼ 0, symmetric or antisymmetric if K is a nonzero integer multiple of three, and degenerate if K is not an integer multiple of three (this includes the half-integer cases referred to above).
