Baer M., Billing G.D. (eds.) - The role of degenerate states in chemistry (Adv.Chem.Phys. special issue, Wiley, 2002)

Vibronic Species of the Vibrational States of Li3 with Consideration of Geometric Phase Effecta

aFor simplicity, the left superscripts v and ev are omitted in denoting the vibrational and vibronic states.

bIn this assignment, we keep the symmetry species of the vibronic state in D3h but indicate the vibrational quantum numbers for the C2v normal modes. The energy increases from left to right, and up to down.

using the Li3 double many-body expansion [58,60,71] potential energy surface (DMBE III [69,70]) are shown in Tables XIV and XV.

Now consider the splitting of the potential energy surface for nontotally symmetric (i.e., vE0 in D3h) displacements of the nuclei. For such geometries the symmetry is lower, and in general the electronic states become nondegenerate (e.g., eA1 eB2 in C2v) instead of being doubly degenerate (eE0 in D3h). Thus, for displaced positions of the nuclei, we obtain two nondegenerate electronic states of different energy. Jahn and Teller [72] were the first to show that, for a nonlinear molecule, there is always one nontotally symmetric normal mode at least that causes a splitting of the potential energy surface such that the minima do not occur at the most symmetric geometry. They are rather at a certain distance from the most symmetric configuration, with the distance increasing with the magnitude of the vibronic interaction. Consequently, several equivalent minima arise on the potential energy surface for unsymmetric molecular conformations. If the vibronic interaction is strong, a significant amount of vibrational energy may then be required to bring the molecule from one minimum to another, and hence one must regard the molecule as nonsymmetric. Conversely, for weak vibronic interactions, only a small amount of vibrational energy may suffice to make the system flow from one minimum to another. In this case, the molecule may be regarded as symmetric, and the vibronic interaction is treated as a perturbation. Appendix E gives a proof of the Jahn– Teller theorem for a X3 molecule following Moffitt and Liehr [73].

The treatment of the Jahn–Teller effect for more complicated cases is similar. The general conclusion is that the appearance of a linear term in the offdiagonal matrix elements Hþ and H þ leads always to an instability at the most symmetric configuration due to the fact that integrals of the type

hc j^þjc i c? c

þ h1 do not vanish there when the product þ has the same species as a nontotally symmetric vibration (see Appendix E). If is the species of the degenerate electronic wave functions, the species of c?þc will be that of 2, which is the symmetric product of with itself. For example, for a D3h molecule, we have the symmetric product ½eE0 ! eE0& ¼ eA01 eE0 (the associated antisymmetric product is feE0 ! eE0g ¼ eA02), and hence it is the vE0 degenerate normal mode that causes the instability since it has the same

symmetry as the eE0 term which arises from the symmetric product. For a D

4h molecule, we have the symmetric product eEg ! eEg ¼ eA1g eB1g eB2g

The Lowest 26 Energy Levels (in eV) for Ground State Li3 with Consideration of the GP Effect

(note that the associated antisymmetric product is feEg ! eEgg ¼ eA2g), and hence it is either the vB1g or vB2g normal modes that cause the instability, since they have the same nontotally symmetric behavior as the eB1g and eB2g terms that arise from the symmetric product.

C.Dynamical Jahn–Teller and Geometric Phase Effects

We begin by discussing the energy levels that arise when a Jahn–Teller instability is present, that is, the dynamic Jahn–Teller effect and the related GP effect. This stems from the observation made by Longuet-Higgins and Herzberg [42–44] that a real-valued electronic wave function changes sign when the nuclear coordinates traverse a closed path encircling a conical intersection. This result has been shown [74] to be valid even for systems that show no symmetry such as LiNaK. In fact, such a geometric phase effect has been rediscovered in a wider context by Berry [21], and hence it is often referred to as the Berry’s

phase effect (as pointed out in the introduction, a further designation [19] is the molecular Aharonov–Bohm effect since it manifests also in the treatment of a charged particle moving in the presence of a magnetic solenoid).

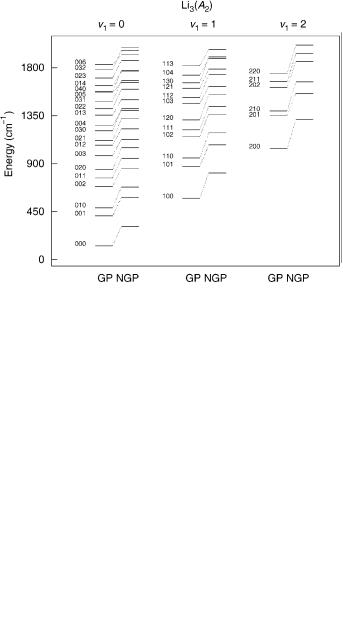
To be specific, we focus this discussion on studies of the vibrational spectrum of ground state Li3, which we have carried out using the DMBE III [69,70] Li3 potential energy surface. All eigenvalues of the system Hamiltonian have been calculated using the MINRES filter diagonalization technique [27]. In turn, the action of the Hamiltonian operator on the nuclear wave function has been evaluated by the spectral transform method in hyperspherical coordinates by using a fast-Fourier transform for r and j and a DVR–FBR transformation for y2. In such studies, the GP effect has also been taken into consideration. Thus, six separate sets of calculations have been performed, which include (1) no consideration of GP effect using a basis set of A1 symmetry; (2) no consideration of GP effect using a basis set of A2 symmetry; (3) no consideration of GP effect using a basis set of E symmetry; (4) consideration of GP effect using a basis set of A1 symmetry; (5) consideration of GP effect using a basis set of A2 symmetry; (6) consideration of GP effect using a basis set of E symmetry. The total number of calculated eigenvalues amounted to 3524 without consideration of GP effect, and 3211 with consideration of GP effect. The full spectra have therefore been calculated, which cover the full range of energies up to the threshold for Li2ðX1 þg Þ þ Li dissociation. Of the total number of calculated vibrational levels, 953 (920), 750 (817), and 1621 (1474) have been found to belong to A1, A2, and E symmetries when GP effects were not (were) taken into consideration. Figures 6–8 show the lowest 40 calculated levels of A1; A2; and E symmetries and the corresponding assignments. As one would expect, each vibrational level is associated to three different vibronic

levels, for example, the (0,0,0) vibrational level in C2v is related to the vA01ð0; 0; 0Þ, vA02ð0; 0; 0Þ, and vE0ð0; 0; 0Þ levels in D3h. Note that in an obvious

evA01ðv1; v2; v3Þ, and evE0ðv1; v2; v3Þ; see Tables XIII–XV. Note also that the notation ðv1; v2; v3Þ implies that the quantum numbers are associated to the symmetric stretching, bending, and asymmetric streching vibrational modes in C2v. They are of A1, A1, and B2 symmetries, respectively; the correlation between the assignments in D3h and C2v is given in Table XIII.

For very small vibronic coupling, the quadratic terms in the power series expansion of the electronic Hamiltonian in normal coordinates (see Appendix E) may be considered to be negligible, and hence the potential energy surface has rotational symmetry but shows no separate minima at the bottom of the moat. In this case, the pair of vibronic levels A1 and A2 in S3 become degenerate by accident, and the D3h quantum numbers ðv1; v2; l2Þ may be used to label the vibronic levels of the X3 molecule. When the coupling of the

Figure 8. As in Figure 6 for the lowest 40 bound states of E symmetry.

vibrational and electronic motions is strong, ðv1; v2; l2Þ are no longer a good set of quantum numbers. In this case, it is more reasonable to think of the vibronic motion as a result of a vibration of an oscillator with C2v symmetry and a rotation corresponding to the motion on the potential valley around the D3h symmetry axis. Such motion may also be viewed as arising from the circular motion of each Li nucleus around their equilibrium positions in the D3h geometry. As we have noted, there is a vibrational angular momentum on the symmetry axis, and hence the rotation of the molecule as a whole is allowed even when the total angular momentum vanishes; indeed, for l2 ¼6 0, the molecule must possess a genuine rotation to compensate the vibrational angular momentum such that J ¼ 0.

The spectra of floppy molecules such as Li3 may therefore have different interpretations. For example, the spectra of specific symmetries have been fitted [11] to within a few percent of error by using the simple vibrational normal mode formula

¼

702 a. j. c. varandas and z. r. xu

where vi are the vibrational quantum numbers, oi are (in energy units) the harmonic frequencies, and xij and yijk are higher order anharmonic corrections. Alternatively, Eq. (59) may be interpreted in terms of pseudorotational energies. According to this interpretation, the first and part of the second summations would represent the pseudorotational energy of a S3 molecule, while the remaining terms would contain the second and higher order coupling pseudorotational terms; the pseudorotational quantum numbers are now defined

about the quantum number m).

Since there are potential barriers along the pseudorotational path, one must also consider the effects due to tunneling. Each specified level then splits into three owing to such tunneling effects. In fact, now we have distinct zero-point energies for each of the three vibronic states, with their energy differences being determined by the pseudorotational motion that includes the tunneling effects.

The vibronic motion may be described by using the ðr; y; jÞ coordinates. In particular, the wave functions for the pseudorotational motion along the hyperangle j that encircles the origin in a X3 system may assume the form [11]

Thus, we can use the approximate quantum number m to label such levels. p

Moreover, it may be shown [11] that (1) m is one-half of an integer for the case with consideration of the GP effect, while it is an integer or zero for the case without consideration of the GP effect; (2) the lowest level must have m ¼ 0 and be a singlet with A1 symmetry in S3 when the GP effect is not taken into consideration, while the first excited level has m ¼ 1 and corresponds to a doublet E; conversely, with consideration of the GP effect, the lowest level must have m ¼ 14 and be a doublet with E symmetry in S3, while the first excited level corresponds to m ¼ 94 and is a singlet A1. Note that such a reversal in the

ordering of the levels was discovered previously by Hancock et al. [59]. Note p

further that jj ¼ m has a meaning similar to the ji quantum numbers described after Eq. (59). The full set of quantum numbers would then be ð jr ; jy; jjÞ,

which could be employed for a description of the vibronic motion. The energies of the vibronic levels will then assume the form

where oi are the frequencies, xjj is the pseudorotational constant for the j motion in energy units, and so on for the other xij and yijk ði; j; k r; y; jÞ coefficients.

Since Li3 in its electronic ground doublet state is a very floppy molecule and the vibrational levels are dense, one may expect the vibrational spectrum to be irregular. To understand such behavior, the Li3 vibrational spectrum has been analyzed statistically with basis on random matrix theory [75]. It has been found [11] that the full spectrum is more regular than each symmetry block per se, which can be understood by recalling that the levels can interact with each other within a symmetry block, while the full spectrum consists of a random superposition of unrelated sequences of energy levels belonging to different symmetries. As discussed in detail elsewhere [11], the spectrum is found to be quasiregular in short range and quasiirregular in long range. It should also be mentioned that the interactions among the levels of the same symmetry result mainly from the so-called Fermi resonances that occur when two or more levels become nearly degenerate and have the same symmetry. Fermi resonances are produced by the anharmonicity of the potential energy surface and make neardegenerate levels (in the harmonic-oscillator approximation) to repel each other. Thus, they originate extra irregularity in the spectrum of a specific symmetry.

One may think that the dynamical Jahn–Teller effect is equivalent to take into consideration the GP effect that arises, for example, due to the conical intersection in X3-type systems formed from 2S atoms. We find it pedagogical from our calculations for Li3 to distinguish three situations. The first corresponds to the calculations in sets (1)–(3) mentioned above, that is, using only one electronic adiabatic BO potential energy surface without consideration of the GP effect. The second refers to the generalized BO treatment in which the GP effect is also considered. Finally, one has the exact (or nearly exact) solution, which is obtained by solving the multistate quantum dynamics (vibronic) problem; see also Section X.D. If one thinks of the first approach as corresponding to include the dynamic Jahn–Teller effect alone, then Table XIV shows that such an effect has a remarkable importance on the vibrational levels as it may be seen by comparing states with equal sets of quantum numbers ðv1; v2; v3Þ in the C2v point group. In turn, the calculations of sets (4)–(6) would include both the dynamic Jahn–Teller and GP effects. The difference between the above two series of results were then attributable to the GP effect alone; see Figures 6–8. This is found [11] to lead to further shifts of

the energy levels, while playing a significant role in the bound vibrational states of Li3, not only quantitative but also qualitative.

Note that all genuine vibronic degeneracies remain no matter how strong the vibronic interaction is, due to the fact that the permutation–inversion symmetry is unchanged, and hence the potential function retains its original symmetry. For example, the degenerate evE0 vibronic levels cannot split even when large amplitude motions are possible. Only the interaction with rotation can produce such a splitting [28].

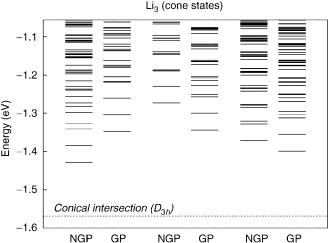
Next, we discuss the J ¼ 0 calculations of bound and pseudobound vibrational states reported elsewhere [12] for Li3 in its first-excited electronic doublet state. A total of 1944 (1675), 1787 (1732), and 2349 (2387) vibrational

states of A , A , and E symmetries have been computed without (with) consi-

1 2 Pþ

deration of the GP effect up to the Li2ðb3 u Þ þ Li dissociation threshold of0:0422 eV. Figure 9 shows the energy levels that have been calculated without consideration of the GP effect up to the dissociation threshold of the lower surface, 1:0560 eV, in a total of 41, 16, and 51 levels of A1, A2, and E symmetries. Note that they are genuine bound states. On the other hand, the cone states above the dissociation energy of the lower surface are embedded in a continuum, and hence appear as resonances in scattering experiments or longlived complexes in unimolecular decay experiments. They are therefore pseudobound states or resonance states if the full two-state nonadiabatic problem is considered. The lowest levels of A1, A2, and E symmetries lie at 1:4282,

Figure 9. Vibrational levels of the first-excited state Li3 calculated without consideration (NGP) and with consideration (GP) of geometric phase effect [12].

1:2729, and 1:3716 eV, respectively; the minimum energy of the conical intersection seam is 1:5692 eV. Dynamical Jahn–Teller effects are therefore seen to have a drastic influence on the vibrational levels (resulting in energy shifts of "0:1 eV). As one would expect, the lowest level in the complete spectrum without consideration of GP effects has A1 symmetry [11].

The assignment of vibrational quantum numbers to the fundamental modes has been done by inspection of the corresponding nuclear probability density plots. Similarly to the plots obtained for the lower sheet [11], the nuclear probability densities of A1 and A2 symmetries show a threefold symmetry, while each component of E symmetry has twofold symmetry about the line b ¼ 0. The nuclear probability densities of the lowest vibrational states concentrate at narrower regions than the corresponding states for the lower sheet, which reflects the fact that the topographies of the two sheets of the potential energy surface are quite different. Although the lowest 100 levels or so obtained for the lower sheet of the potential energy surface could be fit reasonably well using a C2v normal mode expansion, this is not at all the case for the levels in the upper sheet where only the few lowest levels can be unambigously assigned. Indeed, the higher states are rather anharmonic, and nearly degenerate vibrational states occur frequently. Thus, the normal mode scheme employed for the assignment of the vibrational levels in the lower sheet cannot be used in this case, a difficulty that can be attributed to the conical intersection seam. Note that the five lowest levels of A1 symmetry have been assigned by ascending order of energy as ð0; 00Þ, ð1; 00Þ, ð2; 00Þ, ð0; 11Þ, and ð3; 00Þ. Note especially that the notation ðv1; vl22 Þ is used here (and hereafter) to denote the quantum numbers for the symmetric stretching mode (v1), the degenerate mode (v2), and vibrational angular momentum (l2) [28] referring to D3h. Similarly, the five lowest levels of A2 symmetry have been assigned by ascending energy to ð0; 00Þ, ð1; 00Þ, ð2; 00Þ, ð0; 11Þ, and ð3; 00Þ. In turn, the four lowest levels of E symmetry are ð0; 00Þ, ð1; 00Þ, ð0; 11Þ, and ð2; 00Þ, again by ascending order in energy. Thus, the fundamental frequencies for the symmetric stretching mode (A1 symmetry in the D3h point group) are 354.26, 351.01, and 353:34 cm 1 for the A1, A2, and E symmetries in the S3 permutational group, respectively. In turn, the fundamental frequencies for the degenerate mode (E symmetry in the D3h point group) are 824.62, 696.41, and 410.35 cm 1 for A1, A2, and E symmetries in S3, respectively.

Similar calculations with consideration of the GP effect have also been reported [12]. A total of 24, 24, and 50 levels of A1, A2, and E symmetries have been found below the dissociation threshold of the lower surface, 1:0560 eV. These are therefore genuine bound states; the cone states lying above such a dissociation threshold are pseudobound states. The lowest levels of A1, A2, and E symmetries are found to lie at 1:3475, 1:3438, and 1:3989 eV, respectively. The notable feature is that the energy levels have been shifted due to the