1 Алексеев Чеснокова Основы работы в MathCAD

Алексеев Е.Р., Чеснокова О.В

7.5. Решение нелинейных оптимизационных задач

Решение нелинейных задач оптимизации в MathCAD мало чем отличается от линейных. Точно так же надо определить функцию цели, в решающем блоке указать ограничения и обратиться к функциям Minimize или Maximize.

С помощью функции Minimize пользователь MathCAD получает еще один способ решения систем нелинейных уравнений.

Пусть задана система n алгебраических уравнений с n неизвестными.

Задача решения системы (7.12) эквивалентна нахождению минимума функции

эквивалентно решению системы (7.12). Рассмотрим этот метод решения систем нелинейных уравнений на конкретном примере.

ЗАДАЧА 7.8. Решить систему нелинейных алгебраических уравнений

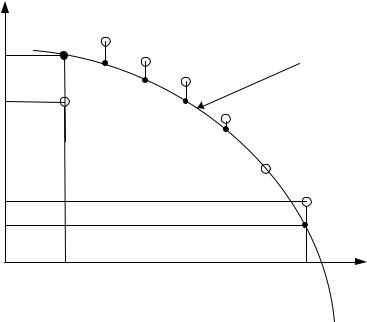
На рис. 7. 15 представлено решение задачи 7.8 с комментариями

Рис. 7.15. Решение системы нелинейных уравнений с помощью функции

Minimize

101

Алексеев Е.Р., Чеснокова О.В

8. Обработка результатов эксперимента в MathCAD

В разделе рассматривается решение задач по обработке реальных количественных экспериментальных данных, полученных в результате всевозможных научных опытов, технических испытаний, астрономических, геодезических и т.п. наблюдений.

8.1. Метод наименьших квадратов

Метод наименьших квадратов позволяет по экспериментальным данным подобрать аналитическую функцию, которая проходит как можно ближе к экспериментальным точкам.

8.1.1. Постановка задачи

Врезультате эксперимента были получены некоторые данные, представленные

ввиде таблицы (табл. 8.1).

Таблица 8.1. Экспериментальные данные

Необходимо построить аналитическую зависимость, наиболее близко описывающую результаты эксперимента.

Идея метода наименьших квадратов заключается в том, что функцию

Y = f(x, a0 a1, ..., ak)

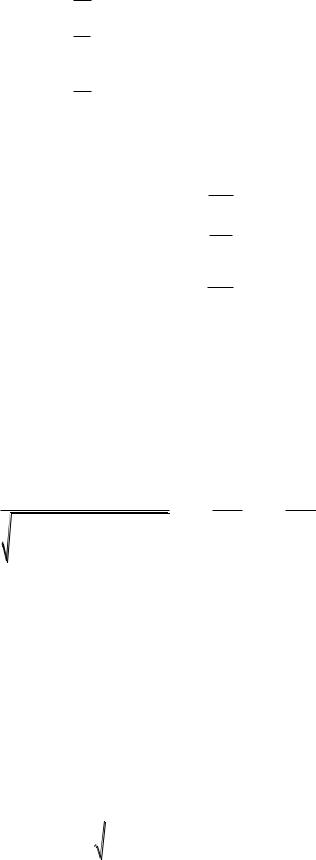
необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений yi от расчетных Yi была наименьшей (см. рис. 8.1):

Рис. 8.1. Геометрическая интерпретация метода наименьших квадратов

102

Алексеев Е.Р., Чеснокова О.В

Задача сводится к определению коэффициентов ai из условия (8.1). Для ее решения необходимо составить систему уравнений

Если параметры ai входят в зависимость Y = f(x, a0 a1, ..., ak) линейно, то получим систему из k+1 линейного уравнения с k+1 неизвестным:

Одной из наиболее часто используемых в методе наименьших квадратов функций является прямая, описываемая уравнением вида y = a0 + a1x, которая называется линией регрессии y на x. Параметры a0 и a1 называются

коэффициентами регрессии.

Существует показатель, характеризующий тесноту линейной связи между x и y, называемый коэффициентом корреляции и рассчитываемый по формуле:

Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки. Если коэффициент корреляции близок к нулю, то это означает, что между x и y не существует линейной связи, но между ними может существовать зависимость, отличная от линейной.

Для того чтобы проверить, значимо ли отличается от нуля коэффициент корреляции, можно использовать критерий Стьюдента. Вычисленное значение критерия определяется по формуле:

103

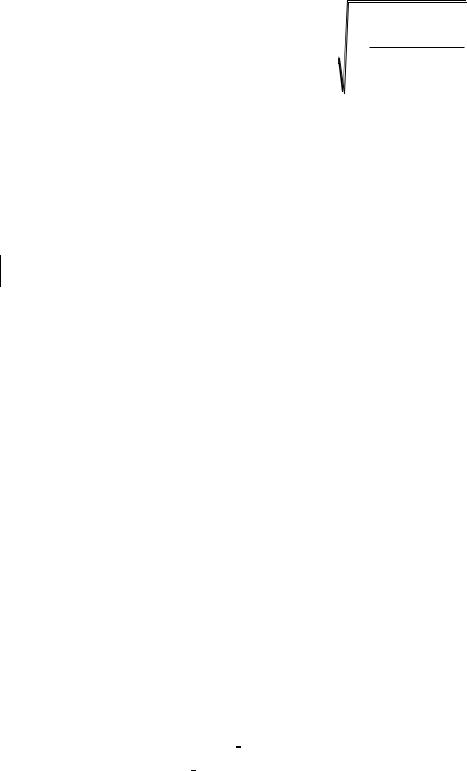
Алексеев Е.Р., Чеснокова О.В

Значение t сравнивается со значением, взятым из таблицы распределения Стьюдента в соответствии с уровнем значимости p и числом степеней свободы k=n–2. Если t больше табличного, то коэффициент корреляции значимо отличен от нуля.

Аналогом коэффициента корреляции r для нелинейных зависимостей является индекс корреляции, рассчитываемый по формуле:

где y – экспериментальные значения, Y – значения, найденные методом наименьших квадратов, My – среднее значение y.

Индекс корреляции по своему абсолютному значению колеблется в пределах от 0 до 1. При функциональной зависимости индекс корреляции равен 1. При отсутствии связи R = 0. Если коэффициент корреляции r является мерой тесноты связи только для линейной формы связи, то индекс корреляции γ – и для линейной, и для криволинейной. При прямолинейной связи коэффициент

8.1.2. Построение линейной зависимости. Определение коэффициента корреляции

Изучение возможностей MathCAD для обработки экспериментальных данных начнем с простейшей задачи подбора линейной зависимости методом наименьших квадратов.

ЗАДАЧА 8.1. В «Основах химии» Д. И. Менделеева приводятся данные о растворимости азотнокислого натрия NaNO3 в зависимости от температуры воды. В 100 частях воды (табл. 8.2) растворяется следующее число условных частей NaNO3 при соответствующих температурах:

Таблица 8.2. Данные о растворимости NaNO3 в зависимости от температуры воды

Необходимо определить, какова будет растворимость азотнокислого натрия при температуре t = 32 в случае линейной зависимости, и определить коэффициент корреляции.

Для определения коэффициентов регрессии a0, a1 в MathCAD существуют следующие функции:

intercept(x,y) возвращает коэффициент регрессии a0;

slope(x,y) возвращает коэффициент регрессии a1.

Для вычисления коэффициента корреляции в MathCAD предназначена функция corr(x,y).

104

Алексеев Е.Р., Чеснокова О.В

В этих функциях x – массив абсцисс экспериментальных точек, y – массив ординат экспериментальных точек.

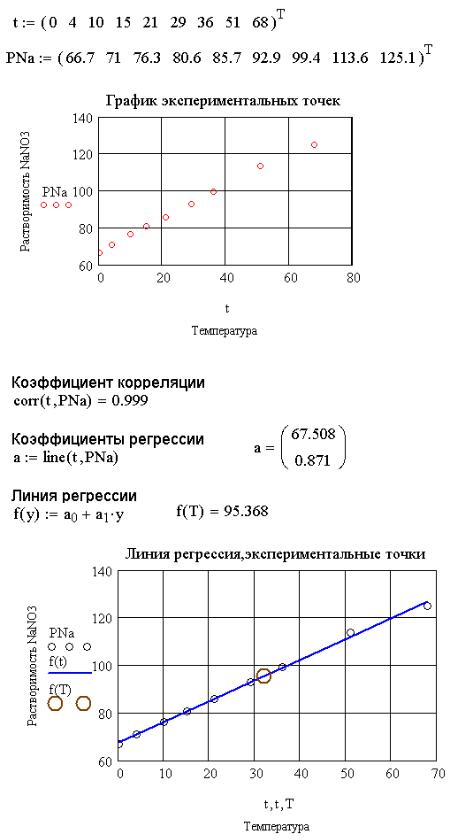
На рис. 8.2 приведено решение задачи 8.1 в MathCAD с комментариями.

Рис. 8.2. Построение линии регрессии и вычисление коэффициента корреляции

105

Алексеев Е.Р., Чеснокова О.В

8.1.3. Построение нелинейной зависимости. Вычисление индекса корреляции

Построение нелинейной аппроксимации рассмотрим на примере решения следующей задачи.

ЗАДАЧА 8.2. Известна табличная зависимость y от х (табл. 8.3).

Таблица 8.3. Табличная зависимость y от x

результаты полученных вычислений.

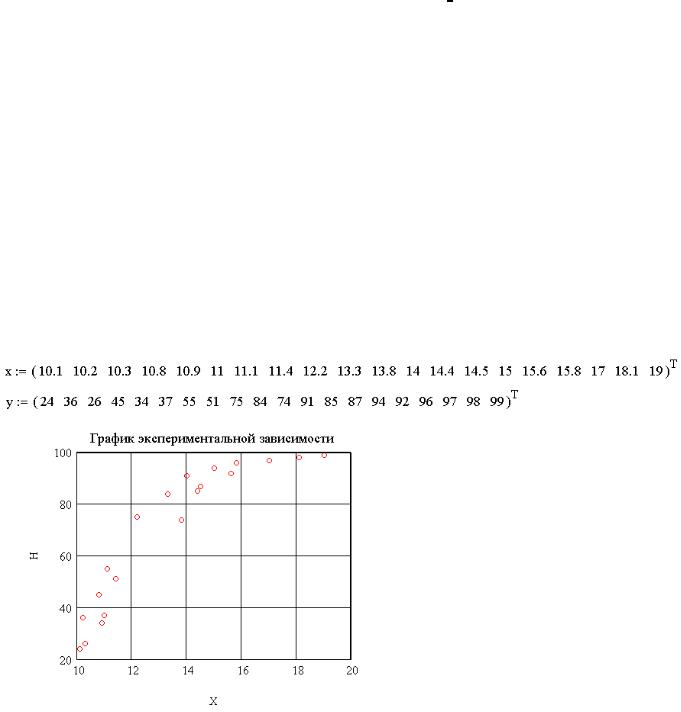
На рис. 8.3. изображен график табличной зависимости y от x.

Рис. 8.3. График экспериментальной зависимости Для построения квадратичной и кубической аппроксимирующей зависимости в

MathCAD можно воспользоваться функциями regress и interp.

Функция regress(x,y,k) возвращает вектор коэффициентов полинома k-й степени, подобранного методом наименьших квадратов по экспериментальным точкам (x – массив абсцисс, y – массив ординат экспериментальных точек).

106

Алексеев Е.Р., Чеснокова О.В

Элементы массива х должны быть упорядочены по возрастанию2. После определения коэффициентов полинома для вычисления значения полинома в конкретных точках можно воспользоваться функцией interp. Функция interp(s,x,y,t) вычисляет значения полинома в точке t, x – массив абсцисс, y – массив ординат экспериментальных точек, s – массив коэффициентов полинома, найденный с помощью функции regress.

С помощью функций regress и interp можно подобрать коэффициенты полного полинома любой степени.

Внимание!!! Функция regress возвращает специальным образом сформированный массив, предназначенный для использования в функции interp, первые три элемента которого являются специальными значениями, используемыми функцией interp, а последующие элементы массива - коэффициентами подобранного полинома.

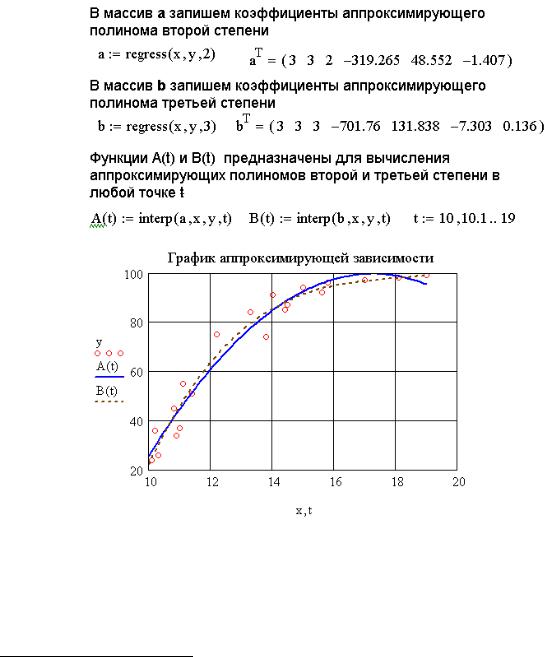
Рис. 8.4. Построение аппроксимирующих зависимостей y a0 a1x a2x2 ,

Для аппроксимации табличной зависимости y(x) полиномами второй и третьей степени необходимо сформировать массивы коэффициентов полиномов a и b, обратившись к функции regress. Далее можно, используя interp,

2 Функции сортировки описаны в третьем разделе

107

Алексеев Е.Р., Чеснокова О.В

построить функции A(t) и B(t), с помощью которых можно вычислить значения аппроксимирующих полиномов второй и третьей степени в любой точке t (рис. 8.4).

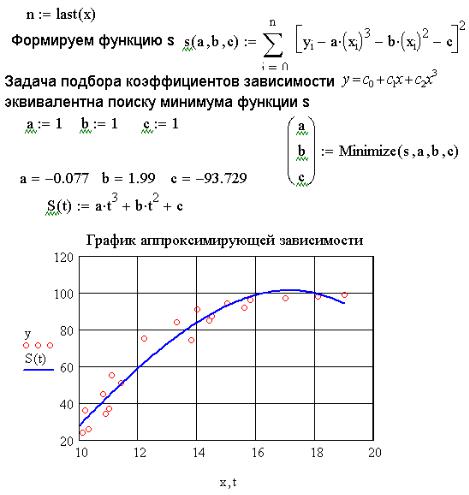
Подобрать зависимость y c0 c1x c2x3 с помощью функций regress и interp не получится. Поэтому вспомним, что аппроксимирующую зависимость необходимо подбирать таким образом, чтобы сумма квадратов отклонений измеренных значений от расчетных была наименьшей. В связи с этим проблема

этой задачи представлено на рис. 8.5.

Таким образом, построены все три зависимости. Осталось определить, какая из них лучше описывает экспериментальные значения, что можно сделать, сравнив индексы регрессии или величины суммы квадратов отклонений.

На рис. 8.6-8.8 представлены расчеты индексов регрессии для трех зависимостей.

Рис. 8.5. Построение аппроксимирующей зависимости y c0 c1x c2x3

108

Алексеев Е.Р., Чеснокова О.В

Рис. 8.6. Вычисление индекса регрессии для квадратичной зависимости

Рис. 8.7. Вычисление индекса регрессии для кубической зависимости

Рис. 8.8. Вычисление индекса регрессии для зависимости y c0 c1x c2x3

109

Алексеев Е.Р., Чеснокова О.В

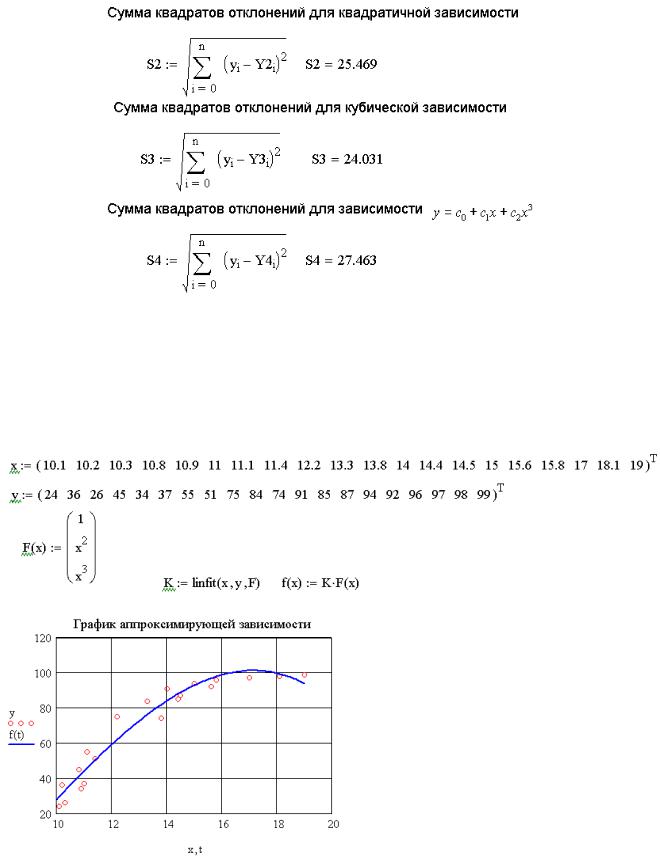
На рис. 8.9 представлены величины сумм квадратов отклонений для всех трех зависимостей.

Рис. 8.9. Вычисление сумм квадратов отклонений подобранных зависимостей Как видно из результатов, приведенных на рис. 8.6-8.9, табличная зависимость,

представленная в табл. 8.3, лучше всего аппроксимируется полиномом третьей степени.

Совет. Представленный на рис. 8.5 метод подбора зависимости является универсальным и подходит для аппроксимации экспериментальных значений любой функцией.

Рис. 8.10. Подбор зависимости с использованием функции linfit

110