1 Алексеев Чеснокова Основы работы в MathCAD

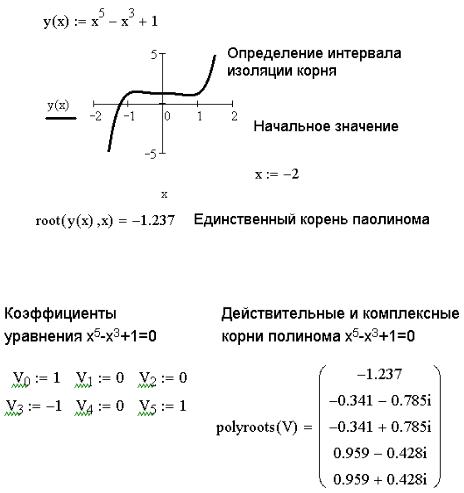
Алексеев Е.Р., Чеснокова О.В

ЗАДАЧА 5.4. Найти решение уравнения y(x)=0, если y(x)=x5–x3+1.

Решим эту задачу при помощи функции root(F(x), x). Для этого выполним следующую последовательность действий:

введем функцию у(x) в рабочий лист;

определим интервал изоляции корня, для чего выполним построение графика функции у(x);

присвоим переменной x значение одного из пределов интервала изоляции, задав тем самым начальное значение;

запишем функцию root(y(x),x) и вычислим корень уравнения.

На рис. 5. 6 приведен ход решения задачи.

Рис. 5. 6. Вычисление действительного корня полинома На рис. 5. 7 показано вычисление всех корней уравнения при помощи функции

polyroots(v). Заметим, среди них есть и мнимые корни.

Рис. 5. 7. Вычисление корней полинома

Далее будет рассмотрено применение функции root(F(x), x) для решения неалгебраических уравнений.

5.1.2. Трансцендентные уравнения

Уравнение, в котором неизвестное входит в аргумент трансцендентных функций (трансцендентные функции – аналитические функции, не являющиеся алгебраическими, например показательные, логарифмические, тригонометрические и т. д.), называется трансцендентным уравнением.

Рассмотрим применение функции root(F(x), x) для решения трансцендентных уравнений.

71

Алексеев Е.Р., Чеснокова О.В

Выражение, стоящее в правой части уравнения, можно представить в виде

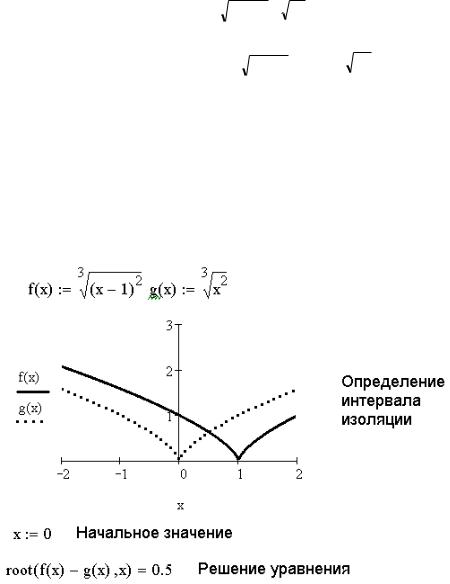
Следовательно, f(x)=g(x), а точка, в которой графики этих функций пересекаются, является графическим решением уравнения. Итак, для решения заданного уравнения (рис. 5.8) выполним следующую последовательность действий:

введем функции f(x) и g(x);

определим интервал изоляции корня;

зададим начальное значение х;

найдем решение при помощи функции root(f(x)–g(x), x).

Рис. 5. 8. Решение трансцендентного уравнения ЗАДАЧА 5.6. Найти корни уравнения f(x)=0.

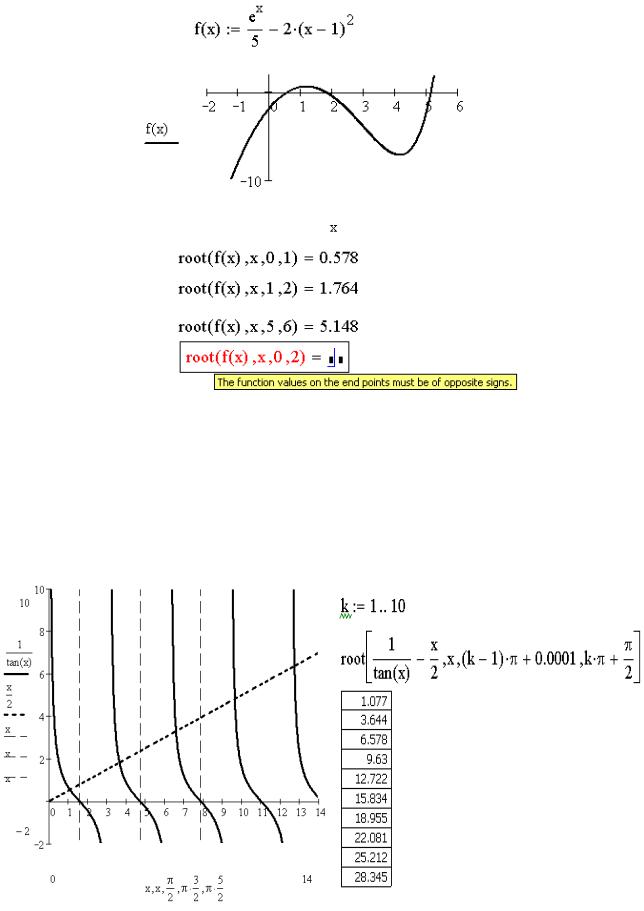
На рис. 5. 9 видно, что график функции f(x) трижды пересекает ось абсцисс, то есть уравнение имеет три корня. Для решения этой задачи воспользуемся тем, что функцию root(f(x), x) можно записать в виде:

root(F(x), x, a, b) – возвращает с заданной точностью значение переменной x, при котором выражение F(x) равно нулю, a и b – пределы интервала изоляции корня.

Понятно, что при такой форме записи функции нет необходимости задавать начальное значение x, так как оно определено в интервале [a,b].

Обратите внимание на последнее обращение к функции root на рис. 5. 11.

MathCAD выдал сообщение об ошибке: «Значения на обоих концах интервала должны иметь противоположные знаки». Произошло это потому, что интервал изоляции задан неверно. На графике видно, что на концах этого интервала функция знак не меняет.

72

Алексеев Е.Р., Чеснокова О.В

Рис. 5. 9. Вычисление корней трансцендентного уравнения

ЗАДАЧА 5.7. Вычислить десять положительных корней уравнения 1/tg(x)–x/2=0. На рис. 5. 10 изображено графическое решение уравнения. Первая точка

пересечения графиков функций 1/tg(x) и x/2 находится в интервале (0; /2), вторая

– ( /2;3 /2), третья – (3 /2;5 /2) и так далее. Следовательно, интервалы изоляции корней заданного уравнения в общем виде можно записать так: ((k-1) ;k + /2), где k – целое число.

Рис. 5. 10. Графическое и аналитическое решение уравнения 1/tg(x)–x/2=0

73

Алексеев Е.Р., Чеснокова О.В

Аналитическое решение уравнения 1/tg(x)–x/2=0 приведено на рис. 5. 10 справа. Обратите внимание на то, как заданы интервалы изоляции корней. Так как функция 1/tg(x) не существует в точках (k-1) , к ним будем прибавлять заведомо очень маленькое число.

5.2. Решение систем нелинейных уравнений

Напомним, что если заданы m уравнений с n неизвестными и требуется найти последовательность из n чисел, которые одновременно удовлетворяют каждому из m уравнений, то говорят о системе уравнений.

Для решения систем уравнений в MathCAD существует так называемый решающий блок. Открывается он ключевым словом Given и имеет следующую структуру:

Начальные условия

Given

Уравнения Ограничительные условия

Выражение, содержащее функцию для решения системы

Рассмотрим назначение каждого из элементов структуры:

Начальные условия – определяют начальные значения искомых переменных и задаются обычным присваиванием;

Уравнения – задаются с применением жирного знака равенства (панель инструментов Boolean) между левой и правой частями уравнения;

Ограничительные условия – задаются в виде неравенств или равенств (панель инструментов Boolean), которые должны выполняться при решении системы уравнений;

Выражение, содержащее функцию для решения системы –

может быть представлено одной из функций: Find, Minerr,

Maximize, Minimize, Odesolve, Pdesolve.

Рассмотрим функции Find и Minerr:

Find (x1,x2, …,xn) – возвращает значение одной или ряда переменных x1,x2, …,xn для точного решения системы;

Minerr(x1,x2, …,xn) – возвращает значение одной или ряда переменных x1,x2, …,xn для приближенного решения системы с

минимальной ошибкой.

Разница между этими функциями заключается в том, что первая используется, когда решение F(x1,x2, …,xn)=0 реально существует, вторая пытается найти такие значения переменных x1,x2, …,xn, при которых функция F(x1,x2, …,xn) будет максимально приближена к нулю. Например, если функция F(x1,x2, …,xn) такова, что при заданной точности вычислений Find выдаст сообщение о том, что решения не существует, то Minerr выдаст значения переменных x1,x2, …,xn, но с меньшей точностью. Применение функций рассмотрим на конкретных примерах.

74

Алексеев Е.Р., Чеснокова О.В

ЗАДАЧА 5.9. Найти уравнение окружности, проходящей через три точки: А(26;4),

В(9;21) и С(17,17).

Уравнение окружности имеет вид: (x–x0)2+(y–y0)2=R2, где M(x;y) – координаты некоторой точки, лежащей на окружности, O(x0;y0) – координаты центра, а R – радиус окружности. Таким образом, задача сводится к отысканию значений x0;y0,

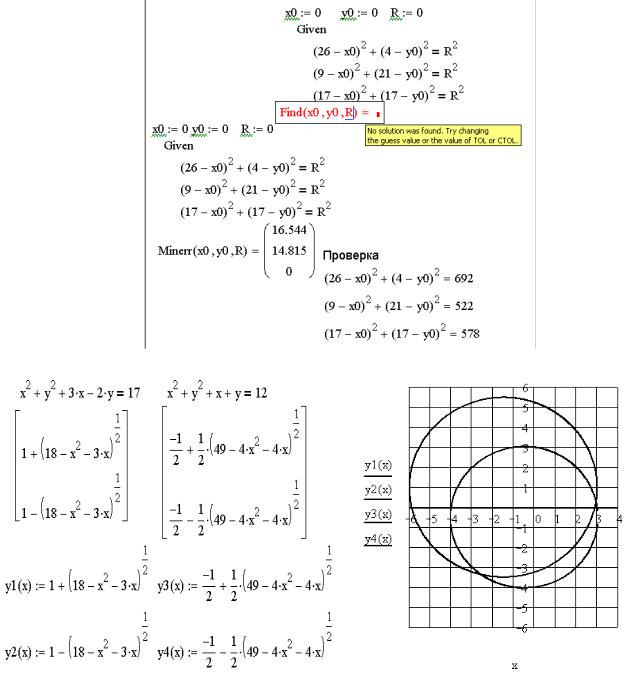
R. Составим систему из трех уравнений и разрешим ее относительно неизвестных x0,y0, R: (26–x0)2+(4–y0)2=R2, (9–x0)2+(21–y0)2=R2, (17–x0)2+(17–y0)2=R2.

На рис. 5. 11 показано решение этой системы при помощи функции Find.

Рис. 5. 11. Решение системы уравнений использованием функции Find Поскольку необходимые параметры найдены, составим уравнение и отобразим

окружность и точки, через которые она проходит, на графике (рис. 5. 12). Последовательность действий следующая:

ввод параметров окружности;

задание уравнения окружности;

запись уравнения в явной форме, то есть выражение у через х при помощи команды Symbolic\Variable\Solve (глава 4, задача 4.3);

определение функций, задающих линии окружности;

ввод координат заданных точек в виде векторов абсцисс и ординат;

создание графика.

На рис. 5. 13 приведено решение рассматриваемой системы уравнений с помощью функции Minerr. Как видим, оно полностью совпадает с решением функцией Find (рис. 5. 11).

На рис. 5. 14 приведен пример некорректного решения поставленной задачи. В начальных условиях переменной R присвоено нулевое значение, то есть предполагается, что радиус окружности равен нулю. При попытке решения функцией Find MathCAD выдает сообщение об отсутствии решений. Minerr решает систему, но предложенное решение не представляет интереса с точки зрения поставленной задачи. Следовательно, решая системы нелинейных уравнений, функцию Minerr использовать нужно осторожно, а начальные значения переменных подбирать как можно точнее.

75

Алексеев Е.Р., Чеснокова О.В

Рис. 5. 12. Графическое решение задачи 5.9

Рис. 5. 13. Решение системы уравнений с использованием функции Minerr

ЗАДАЧА 5.10. Решить систему нелинейных уравнений: x2+y2+3x–2y=17,

x2+y2+x–y=12.

Графическое решение системы приведено на рис. 5. 14.

Очевидно, что система уравнений имеет два решения, так как окружности пересекаются в двух точках. Для определения каждого из них необходимо дважды воспользоваться решающим блоком и соответствующим образом подобрать начальные значения переменных. На рис. 5. 15 показано, как это сделать.

76

Алексеев Е.Р., Чеснокова О.В

Рис. 5. 14. Пример использования функций Find и Minerr

Рис. 5. 14. Графическое решение задачи 5. 10.

ЗАДАЧА 5.11. Решить систему уравнений: x2+y2+3x–2y=4,

x+2y=5.

Данная система легко сводится к одному уравнению при помощи элементарных преобразований (рис. 5.16). Линейное уравнение решается относительно одного из двух неизвестных, например, можно выразить х через у, выполнив команду Symbolic\Variable\Solve при выделенном х. Полученное выражение необходимо подставить в квадратное уравнение и упростить(Symbolic\Variable\Collect).

Решение квадратного уравнения с одним неизвестным, полученного в результате преобразований заданной системы, приведено на рис. 5.17. Графическое решение уравнение показало, что имеется два действительных корня. Поэтому решающий блок используется дважды с соответствующими

77

Алексеев Е.Р., Чеснокова О.В

начальными значениями. Эта задача была приведена исключительно для демонстрации использования решающего блока для определения корней одного уравнения.

Рис. 5. 15. Численное решение задачи 5. 10.

Рис. 5. 16. Приведение системы из задачи 5. 11 к одному уравнению.

Рис. 5. 17. Решение одного уравнения с помощью решающего блока.

78

Алексеев Е.Р., Чеснокова О.В

5.3. Символьное решение уравнений, систем уравнений и неравенств

Символьные операции можно применять к функциям root и Find. Рассмотрим несколько примеров.

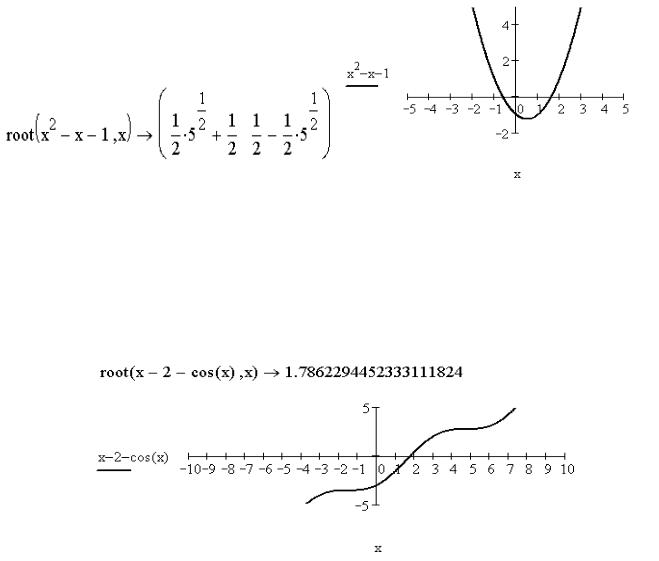
ЗАДАЧА 5. 12. Найти корни полинома x2 x 1 0 .

На рис. 5. 18 показано решение задачи с применением символьной операции Symbolic Evolution на панели инструментов Symbolic к функции root. На этом же рисунке изображен график полинома.

Рис. 5. 18. Решение уравнения из задачи 5.12 Заметим, что повышение степени полинома может привести к громоздкому и

трудно анализируемому результату. Поэтому советуем читателю выбирать метод решения (символьный или численный) в зависимости от постановки задачи и требуемого результата.

ЗАДАЧА 5. 13. Решить трансцендентное уравнение.

Символьное решение уравнения представленное на рис. 5. 19, подтверждено графическим.

Рис. 5. 19. Решение трансцендентного уравнения из задачи 5.13 Но обратите внимание, что не всегда есть смысл прибегать к символьному

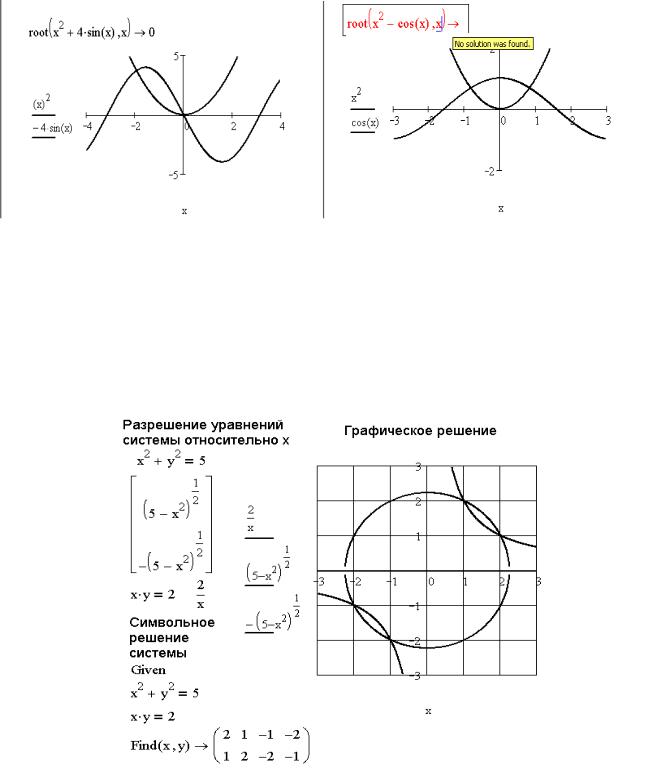
разрешению трансцендентного уравнения. На рис. 5. 20, сверху, приведен пример уравнения, которое реально имеет два корня, но при символьном решении дает только тривиальный.

Кроме того, не для всякого трансцендентного уравнения вообще удается получить символьное решение, хотя численное существует (рис. 5. 20, снизу). Происходит это потому, что символьное решение можно записать только для уравнения, имеющего аналитическое решение, то есть решение, которое может быть представлено в виде формул.

79

Алексеев Е.Р., Чеснокова О.В

Рис. 5. 20. Примеры поиска символьного результата при отсутствии аналитического решения

ЗАДАЧА 5. 14. Решить систему уравнений: x2+y2=5,

x∙y=2.

Графическое и символьное решение системы уравнений приведено на рис. 5. 21. От численного решения символьное отличается тем, что после функции Find ставится стрелка (панель инструментов Symbolic), и оно не требует задания начальных значений.

Рис. 5. 21. Символьное и графическое решение системы уравнений Решать уравнения в MathCAD можно и без использования функции root.

Символьное решение уравнений и неравенств выполняется при помощи операции solve на панели инструментов Symbolic (рис. 5.22) или команды Symbolic\Variable\Solve, которая применялась нами ранее для выражения одной переменной через другую.

80