1 Алексеев Чеснокова Основы работы в MathCAD

Алексеев Е.Р., Чеснокова О.В

Рисунок 3.6. Примеры операций над матрицами

Работа с векторами в MathCAD так же не вызывает затруднений. Вычисления, которые приведены во фрагменте рабочего документа на рисунке 3.7, известны из математического аппарата векторных вычислений.

Внимание!!! Для вычисления длины вектора D (рис.3.7) была использована кнопка Absolute Value (абсолютное значение), расположенная на панели инструментов Calculator, а вычисление определителя матрицы А (рис.3.6) было выполнено при помощи кнопки Determinant (определитель) с панели инструментов Matrix. Визуально эти кнопки не отличаются, но операции, выполняемые ими, различны.

Немного «необычным», с точки зрения классических понятий, может

показаться оператор векторизации, вызываемый кнопкой 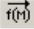. Например, если к выражению sin(M), где M - это вектор, применить этот оператор (рис. 3.8), то результатом вычислений будет вектор, каждый элемент которого равен синусу соответствующего элемента исходного вектора M. В качестве еще одного примера использования оператора векторизации можно привести умножение векторов M и K (рис.3.8). Как известно, выражение M∙K дает скалярное

31

Алексеев Е.Р., Чеснокова О.В

произведение заданных векторов, а это же произведение под знаком длинной стрелки создает новый вектор, каждый элемент которого равен произведению соответствующих компонент исходных векторов.

Рисунок 3.7. Примеры векторных операций

Рисунок 3.8. Примеры векторизации векторов и матриц

32

Алексеев Е.Р., Чеснокова О.В

Внимание!!! В ранних версиях MathCAD функции, аргументами которых могут быть только скалярные переменные, например, sin(M), можно было использовать при работе с векторами только с применением оператора векторизации. Теперь это не обязательно. Если к выражению sin(M), где M – вектор, не применять векторизацию, то она выполнится автоматически. А вот если аргумент функции – матрица, то применение оператора векторизации обязательно (рис.3.8).

В MathCAD с матрицами можно выполнять символьные операции. Меню символьных операций содержит три функции – транспонирование (Transpose), обращение матрицы (Invert) и вычисление определителя матрицы (Determinant).

Для того чтобы произвести какую либо операцию с использованием меню, матрицу необходимо выделить, а затем выбрать необходимый пункт меню щелчком мыши. Фрагмент рабочего листа MathCAD, содержащий символьные операции над матрицей, приведен на рис. 3.9.

Рисунок 3.9. Символьные операции над матрицей Кроме панели инструментов и пунктов меню для работы с матрицами, в

MathCAD существуют специальные функции, которые можно разделить на группы: функции определения матриц и операции с блоками матриц, функции вычисления различных числовых характеристик матриц и функции, реализующие численные алгоритмы решения задач линейной алгебры, функции сортировки. Рассмотрим, наиболее часто используемые функции.

Функции определения матриц и операции с блоками матриц:

matrix(m,n,f) – создает и заполняет матрицу A={aij} размерности m на n, каждый элемент которой aij равен значению функции f(i,j), пример приведен на рис.3.10;

diag(v) – создает диагональную матрицу (рис.3.11), элементы главной диагонали которой хранятся в векторе v;

identity(n) – создает единичную матрицу (рис.3.12) порядка n;

augment(A,B) – из матриц А и В формируется третья матрица (рис.3.13), первые столбцы которой содержат матрицу А, а последние - матрицу В (матрицы А и В должны иметь одинаковое число строк);

33

Алексеев Е.Р., Чеснокова О.В

Рисунок 3.10. Создание матрицы, каждый элемент которой формируется по заданной функции

Рисунок 3.11. Формирование диагональной матрицы

Рисунок 3.12. Создание единичной матрицы

Рисунок 3.13. Формирование матрицы при помощи функции augment(A,B)

stack(A,B) – из матриц А и В формируется третья матрица (рис.3.14), первые строки которой содержат матрицу А, а последние - матрицу В (матрицы А и В должны иметь одинаковое число столбцов);

submatrix(A,l,k,p,r) – формирует матрицу (рис.3.15), которая является блоком матрицы А, расположенным в строках с l по k и в столбцах с p по r (l<k, p<r);

Re(A) – возвращает матрицу (вектор) действительных частей матрицы (вектора) А с комплексными элементами (рис.3.16);

Im(A) – возвращает матрицу (вектор) мнимых частей матрицы (вектора) А с комплексными элементами (рис.3.16).

34

Алексеев Е.Р., Чеснокова О.В

Рисунок 3.14. Формирование матрицы при помощи функции stack(A,B)

Рисунок 3.15. Формирование матрицы при помощи функции submatrix(A,l,k,p,r)

Рисунок 3.16. Применение функций Re(A) и Im(A)

Функции вычисления различных числовых характеристик матриц:

last(v) – вычисление номера последней компоненты вектора v;

length(v) – вычисление количества компонент вектора v;

rows(A) – вычисление числа строк в матрице А;

cols(A) – вычисление числа столбцов в матрице А;

max(A) – вычисление наибольшего элемента в матрице (векторе) А;

min(A) – вычисление наименьшего элемента в матрице (векторе) А;

mean(A) – вычисление среднего значения матрицы (вектора) А;

median(A) – вычисление медианы матрицы (вектора) А;

tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;

ranc(A) – вычисление ранга матрицы А;

norm1(A) – вычисление первой нормы ||A||1 квадратной матрицы

А={aij};

norm2(A) – вычисление второй нормы ||A||2 квадратной матрицы

А={aij};

norme(A) – вычисление евклидовой нормы ||A||e квадратной матрицы

А={aij};

normi(A) – вычисление бесконечной нормы ||A||i квадратной матрицы

А;

cond1(A) – определяет число обусловленности матрицы, вычисленное в первой норме ||A||1;

35

Алексеев Е.Р., Чеснокова О.В

cond2(A) – определяет число обусловленности матрицы, вычисленное во второй норме ||A||2;

condi(A) – определяет число обусловленности матрицы, вычисленное

вбесконечной норме ||A||i;

conde(A) – определяет число обусловленности матрицы, вычисленное

вевклидовой норме ||A||e.

Примеры применения этих функций приведены на рис.3.17.

Рисунок 3.17. Применение функций вычисления числовых характеристик матриц

Функции, реализующие численные алгоритмы решения задач линейной алгебры:

rref(A) – приведение матрицы к ступенчатому виду путем элементарных операций со строками матрицы А;

eigenvals(A) – вычисление собственных значений квадратной матрицы А;

eigenvecs(A) – вычисление собственных векторов квадратной матрицы А;

eigenvec(A,p) – вычисление собственного вектора матрицы А, отвечающего собственному значению p;

genvals(A,B) – вычисляет вектор v обобщенных собственных значений, соответствующий решению уравнения A∙x=v∙B∙x;

genvecs(A,B) – вычисляет матрицу, содержащую собственные векторы, соответствующие обобщенным собственным значениям;

geninv(A) – вычисляет матрицу, левую обратную к матрице А, L∙A=E, где Е – единичная матрица размером n×n, L – прямоугольная матрица размером n×m, А – прямоугольная матрица размером m×n;

36

Алексеев Е.Р., Чеснокова О.В

lsolve(A,b) – решение системы линейных алгебраических уравнений

A∙x=b.

lu(A) – выполняет треугольное разложение матрицы А: A=С∙L∙U, где L и U – соответственно нижняя и верхняя треугольные матрицы, все четыре матрицы квадратные и одного порядка;

qr(A) – выполняет разложение матрицы А: A=Q∙R, где Q – ортогональная матрица, а R – верхняя треугольная матрицы;

cholesky(A) – выполняет разложение матрицы А по схеме Холецкого: А=L∙LT, где А - квадратная, симметричная, положительно определенная матрица, L – треугольная матрица;

svd(A) – выполняет сингулярное разложение матрицы А размером n×m: A=U∙S∙VT , где U и V – ортогональные матрицы размером m×m и n× n соответственно, а S – диагональная матрица, на диагонали которой расположены сингулярные числа матрицы А;

svds(A) – вычисляет вектор, содержащий сингулярные числа матрицы

А размером n×m, где n≥m.

Функции сортировки:

sort(v) – сортировка элементов вектора v в порядке возрастания их значений;

reverse(v) – перестановка элементов вектора v в обратном порядке;

csort(A,n) – перестановка строк матрицы А таким образом, чтобы отсортированным оказался n-й столбец;

rsort(A,n) – перестановка столбцов матрицы А таким образом,

чтобы отсортированной оказалась n-я строка.

Применение этих функций будет рассмотрено далее при решении конкретных задач линейной алгебры. И, прежде чем перейти к рассмотрению этих задач, сделаем несколько замечаний по поводу вывода матриц и векторов, полученных в результате вычислений.

На рис.3.19 показано, что матрица, полученная в результате вычислений, может быть выведена в стандартном матричном виде и в виде таблицы с нумерацией строк и столбцов.

Если не указано иначе, MathCAD определяет автоматически, в каком виде отображать матрицу или вектор. Обычно это зависит от их размерности. Например, слишком длинный вектор автоматически выводится в виде таблицы, с полосами прокрутки для просмотра, так, как показано на рис.3.29.

Для того, чтобы изменить вид отображаемой информации, необходимо выполнить следующие действия:

вызвать диалоговое окно Result Format, дважды щелкнув в области выведенной матрицы или вектора;

выбрать вкладку Display Options;

в поле Matrix display style установить необходимый формат вывода – Automatic (формат определяется автоматически), Matrix (представить в

37

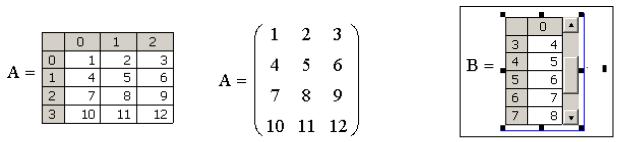
Алексеев Е.Р., Чеснокова О.В

матричном виде), Table (представить в виде таблицы) и нажать кнопку

OK.

3.3. Задачи линейной алгебры

Описанные выше векторные и матричные функции и операторы MathCAD позволяют решать широкий круг задач линейной алгебры. Рассмотрим некоторые из них.

3.3.1. Решение некоторых задач алгебры матриц

Перейдем к конкретным задачам.

ЗАДАЧА 3.1. Для матриц А, В и С проверить выполнение следующих тождеств: (А∙В)∙С=А∙(В∙С) и (АТ+В) С=АТ∙С+В∙С. Решение на рис.3.20.

ЗАДАЧА 3.2. Упростить выражение ∆А-3∙∆В+2∙х–10, где ∆А и ∆В - определители матриц А и В соответственно.

На рисунке 3.21 показано, как можно решить эту задачу, воспользовавшись символьными операциями MathCAD.

ЗАДАЧА 3.3. Проверить, является ли матрица симметрической (АТ=А). Решение приведено на рис.3.22.

ЗАДАЧА 3.4. Проверить, является ли матрица ортогональной (если |A|=detA≠0

и АТ=А-1).

Для решения этой задачи необходимо вычислить определитель заданной матрицы, и убедиться в том, что он не равен нулю. Затем транспонировать исходную матрицу и найти обратную к ней. Если визуально сложно убедиться в том, что транспонированная матрица равна обратной, можно вычислить их разность. В результате должна получиться нулевая матрица (рис.3.23).

ЗАДАЧА 3.5. Проверить, является ли матрица А идемпотентной (А2=А). Показать, что матрица В=2А-Е, где Е – единичная матрица, инволютивна (А2=Е, где Е – единичная матрица).

Для того, чтобы выяснить, является ли матрица А идемпотентной, ее необходимо возвести в квадрат и сравнить с исходной. В формировании матрицы В участвует единичная матрица, которую можно получить при помощи описанной выше функции identity(n). Определить, является ли матрица В инволютивной, можно, сравнив ее с единичной матрицей. Подробно решение задачи приведено на рис. 3.24.

38

Алексеев Е.Р., Чеснокова О.В

Рисунок 3.20. Решение задачи 3.1

Рисунок 3.21. Решение задачи 3.2

39

Алексеев Е.Р., Чеснокова О.В

Рисунок 3.22. Решение задачи 3.3

Рисунок 3.23. Решение задачи 3.4

Внимание!!! Операция возведения в целую неотрицательную степень определена только для квадратных матриц, так как при выполнении этой

операции матрица умножается сама на себя заданное количество раз: А0=Е,

А1=А, А2=А∙А, А3=А∙А∙А,…

ЗАДАЧА 3.6. Решить матричные уравнения А∙Х=В и Х∙A=B, выполнить проверку.

Матричное уравнение - это уравнение вида А∙Х=В или Х∙А=В, где Х - это

неизвестная матрица. Если умножить матричное уравнение на матрицу, обратную к А, то оно примет вид: А-1 А Х=А-1 В или Х А А-1=В А-1. Так как А-1 А=А А-1=Е, а

Е∙Х=Х∙Е=Х, то неизвестную матрицу Х можно вычислить так: Х=А-1 В или Х=В А- 1. Понятно, что матричное уравнение имеет единственное решение, если А и В –

40