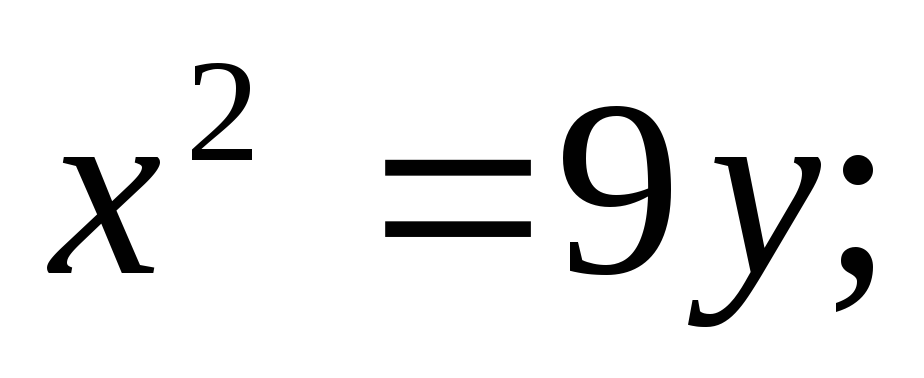- •Глава 2.
- •Векторная алгебра и
- •Аналитическая геометрия
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9 Известны середины трех сторон квадрата . Найдите середину четвертой стороны .
- •Задание 10
- •Задание 11
- •Задание 12
- •Задание 13
- •Задание 14
- •Задание 15
- •Задание 16
- •Задание 17
- •Задание 18
- •Задание 19 Найдите координаты вектора , перпендикулярного векторами.
- •Задание 20
- •Задание 24
- •Задание 25
- •Задание 26
- •Задание 27
- •Задание 28
- •Задание 29
- •Задание 30
- •Задание 31
- •Задание 32
- •Задание 33
- •Задание 34
- •Задание 35
- •Задание 36.
- •Задание 37
- •Задание 38
- •Задание 39
- •Задание 40
- •Задание 41
- •Задание 42
- •Задание 43
- •Задание 44
- •Задание 45
- •Задание 47.
- •Задание 48
- •Задание 49
- •Задание 56
- •Задание 57
- •Задание 58
- •Задание 59
- •Задание 60
- •Задание 61
- •Задание 62 Известны середины трех сторон квадрата . Найдите середину четвертой стороны .
- •Задание 63
- •Задание 64 Даны уравнения прямых , и точка. Требуется:
- •Задание 65
- •Задание 66
- •Задание 67
- •Задание 68
- •Задание 69 Напишите уравнение плоскости, проходящей через три данные точки:
- •Задание 70
- •Задание 71
- •Задание 72
- •Задание 73
- •Задание 74
- •Задание 75
- •Задание 76
- •Задание 77
- •Задание 78
- •Задание 79
- •Задание 80
- •Задание 81
- •Задание 82
- •Задание 83
- •Задание 84.
- •Задание 85
- •Задание 86
- •Задание 87
- •Задание 88
- •Задание 89
- •Задание 90
- •Задание 91
- •Задание 92
- •Задание 93
- •Задание 94
- •Задание 95
- •Задание 96
- •Задание 97
- •Задание 98
- •Задание 99
- •Задание100
- •Задание 101
- •Задание 102
- •Задание 103
- •Задание 104
- •Задание 105
- •Задание 106
- •Задание 107
- •Задание 108
Задание 92
Найдите ортогональную
проекцию точки
![]() на прямую
на прямую![]() .
.
|
|
|
|
|
|
|
|
1. |
(8 , -6 , 4) |
-5x +9y = -21 6x +9z = 99
|
6. |
(1 , 3 , 4) |
3x - 8y = -8 4x - 8z = -136
|
|
2. |
(-8 , -7 , -5) |
8x - 5y = 66 7x - 5z = 29
|
7. |
(9 , 3 , 7) |
-7x - 3y = 375 -10x - 3z = 339
|
|
3. |
(5 , -8 , -6) |
5x +2y = 101 -7x +2z = -183
|
8. |
(7 , -5 , -9) |
-7x - 5y = 368 -2x - 5z = 113
|
|
4. |
(1 , -10 , -5) |
-7x +2y = 38 -5x +2z = 72
|
9. |
(9 , 1 , -1) |
6x - 2y = 66 3x - 2z = 100
|
|
5. |
(-6 , -10 , -5) |
-3x +y = 68 -7x +z = 229
|
10. |
(6 , 7 , 5) |
-3x - 9y = 225 7x - 9z = -369
|
Задание 93
Найдите ортогональную
проекцию точки
![]() на прямую
на прямую![]() :
:
|
|
|
|
|
|
|
|
1. |
(-8 , 8 , -5) |
x = 10t -7 , y = -6t + 26 , z = 2t + 1 |
6. |
(1 , -9 , 9) |
x = -7t -35 , y = 8t -21 , z = 4t + 1 |
|
2. |
(3 , 0 , -5) |
x = 3t + 11 , y = t -16 , z = 8t -10 |
7. |
(-4 , -2 , 6) |
x = -9t -1 , y = -3t + 38 , z = -6t -15 |
|
3. |
(-2 , 4 , -1) |
x = 7t + 20 , y = 5t -14 , z = -t + 13 . |
8. |
(2 , 4 , -6) |
x = 7t -23 , y = 9t -24 , z = 10t + 35 |
|
4. |
(4 , 9 , -9) |
x = -5t + 3 , y = 8t -30 , z = 6t -23 |
9. |
(-2 , -9 , -10) |
x = -9t + 36 , y = 7t -30 , z = 8t -35 |
|
5. |
(-7 , -5 , -8) |
x = -t -14 , y = 9t -20 , z = -4t -32 . |
10. |
(-10 , 9 , 10) |
x = -6t -33 , y = -t + 28 , z = 5t + 17 |
Задание 94
Найдите ортогональную
проекцию точки
![]() на прямую
на прямую![]() ,проходящей
через точки
,проходящей
через точки![]() и
и![]() .
.
|
|
|
|
|
|
1. |
(-7 , -6 , 2) |
(32 , -38 , 18) |
(40 , -48 , 24) |
|
2. |
(-1 , -1 , 3) |
(35 , 1 , -12) |
(30 , 8 , -16) |
|
3. |
(4 , -3 , -8) |
(20 , -26 , -36) |
(13 , -23 , -30) |
|
4. |
(-8 , -5 , -10) |
(7 , 11 , -12) |
(11 , 4 , -20) |
|
5. |
(-9 , -6 , 3) |
(19 , 18 , 17) |
(18 , 23 , 20) |
|
6. |
(10 , 3 , 2) |
(-31 , -23 , 22) |
(-25 , -13 , 30) |
|
7. |
(-10 , 4 , -8) |
(-7 , 28 , 13) |
(-10 , 21 , 7) |
|
8. |
(0 , -2 , -4) |
(35 , -31 , -16) |
(33 , -26 , -8) |
|
9. |
(-5 , 10 , 7) |
(10 , 33 , -4) |
(4 , 38 , 4) |
|
10. |
(-2 , 6 , 8) |
(20 , -38 , 9) |
(26 , -47 , 14) |
Задание 95
1.
Прямая
![]() параллельна плоскости 2x
+ 6y
- 5z
+ 4 = 0 при p
= ... .
параллельна плоскости 2x
+ 6y
- 5z
+ 4 = 0 при p
= ... .
2.
Прямая
![]() перпендикулярна к плоскости Аx
- 2y
+ 6z
- 1 = 0 при p
= ... , A
= ... .
перпендикулярна к плоскости Аx
- 2y
+ 6z
- 1 = 0 при p
= ... , A
= ... .
3.
Прямая
![]() и плоскость 2х – у +Cz
= 0 не пересекаются при С = … .
и плоскость 2х – у +Cz
= 0 не пересекаются при С = … .
4.
Прямая
![]() и плоскость 5х – 6у -z
= 0 не пересекаются при а
= … .
и плоскость 5х – 6у -z
= 0 не пересекаются при а
= … .
5.
Прямая
![]() и плоскость 4х + Ву +Cz
= 0 взаимно перпендикулярны при B
= …, C
= … .
и плоскость 4х + Ву +Cz
= 0 взаимно перпендикулярны при B
= …, C
= … .
6.
Прямая
![]() и плоскость 2х – 2у –z
+ 1 = 0 взаимно перпендикулярны при n
= …, p
= … .
и плоскость 2х – 2у –z
+ 1 = 0 взаимно перпендикулярны при n
= …, p
= … .
7. Прямая L(x = 5t, y = - t, z = рt) параллельна плоскости x – y – z + 3 = 0 при p = … .
8. Прямая L(Ax – y + z = 0, 2x + 4y + 5z = 0) параллельна плоскости x – z + 2 = 0 при A = … .
9.
Прямая
![]() принадлежит плоскостиAx
– 2y
+ z
– 4 = 0 при c
= …, A
= … .
принадлежит плоскостиAx
– 2y
+ z
– 4 = 0 при c
= …, A
= … .
10.
Прямая
![]() и плоскостьx
– y
+ z
+ D
= 0 параллельны, если n
= …, а D
…
.
и плоскостьx
– y
+ z
+ D
= 0 параллельны, если n
= …, а D
…
.
ЗАДАНИЕ 96. Построить кривые второго порядка по заданным уравнениям.
Варианты:
а)
 б)
б)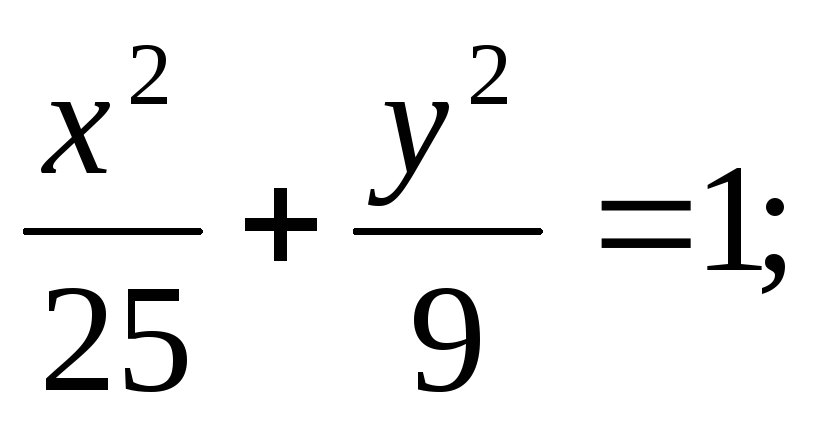 в)
в) г)
г)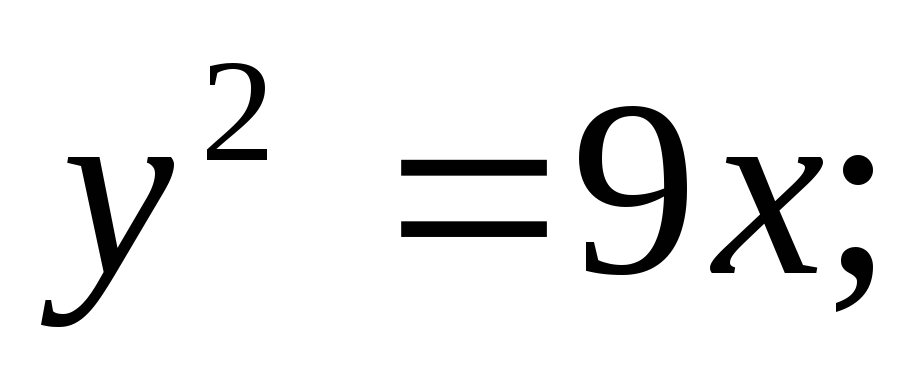
а)
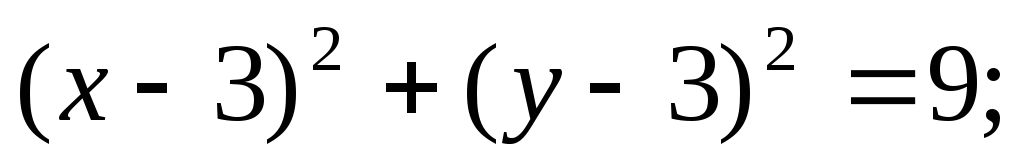 б)
б) в)
в)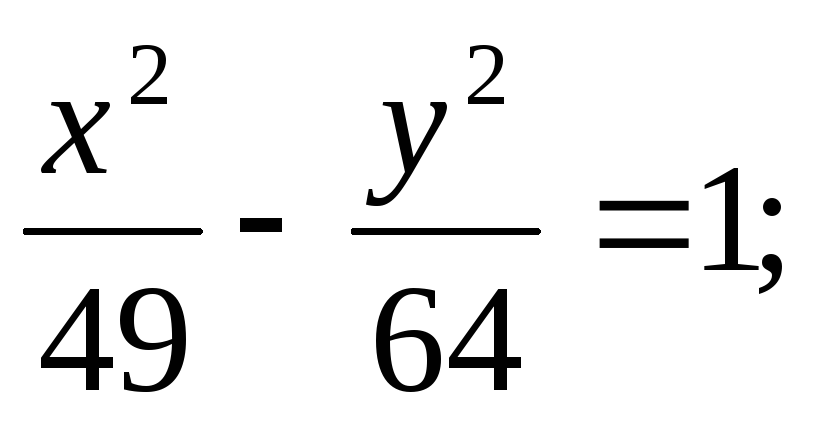 г)
г)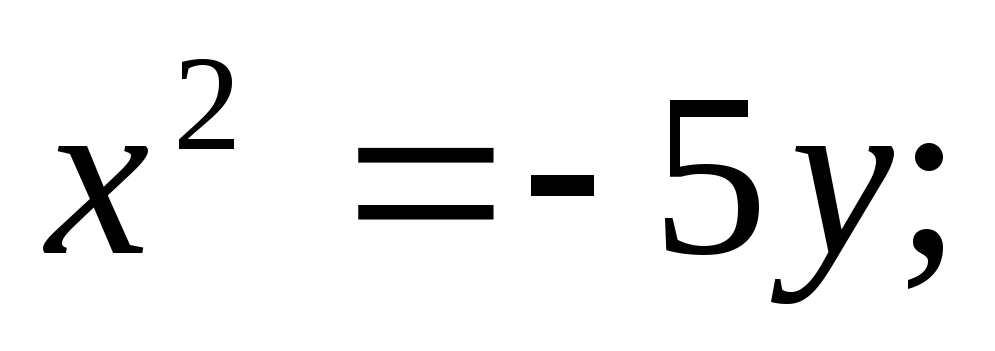
а)
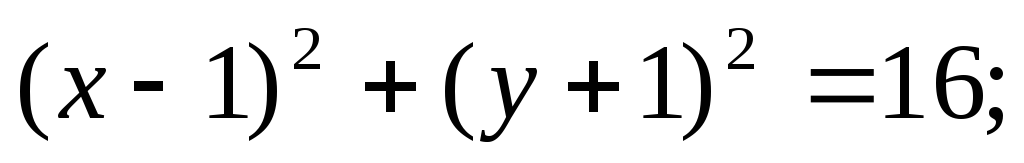 б)
б)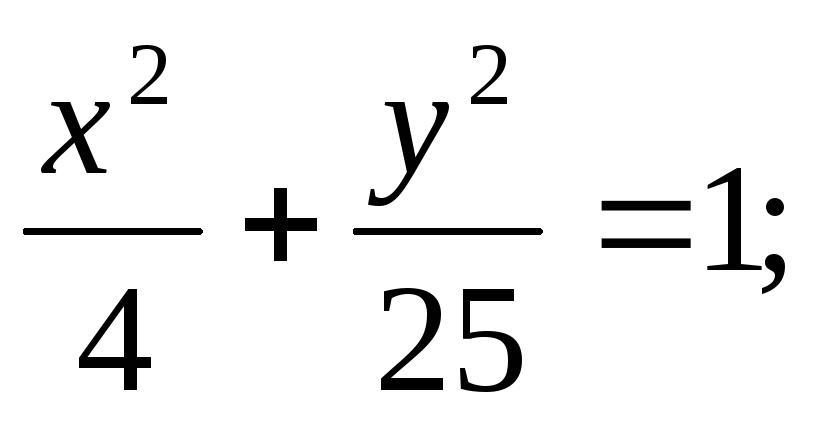 в)
в)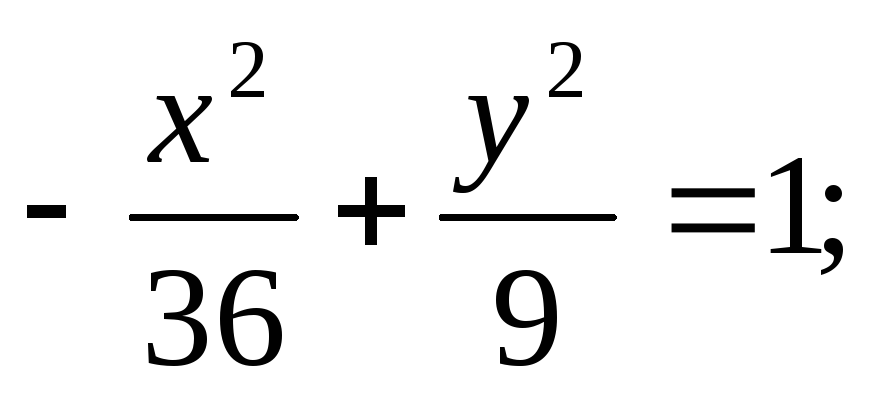 г)
г)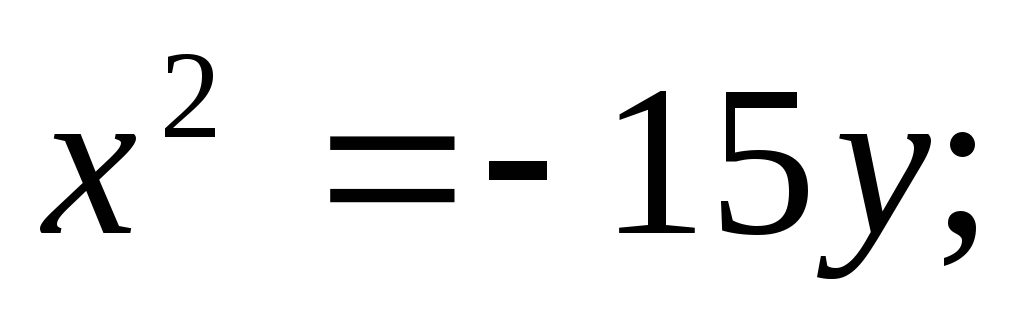
а)
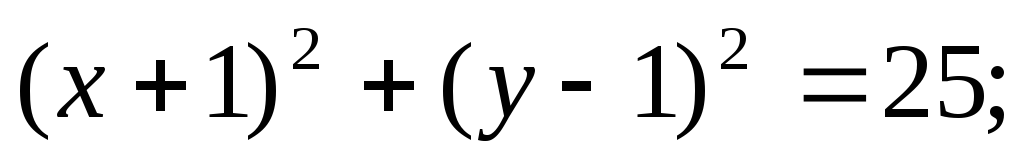 б)
б)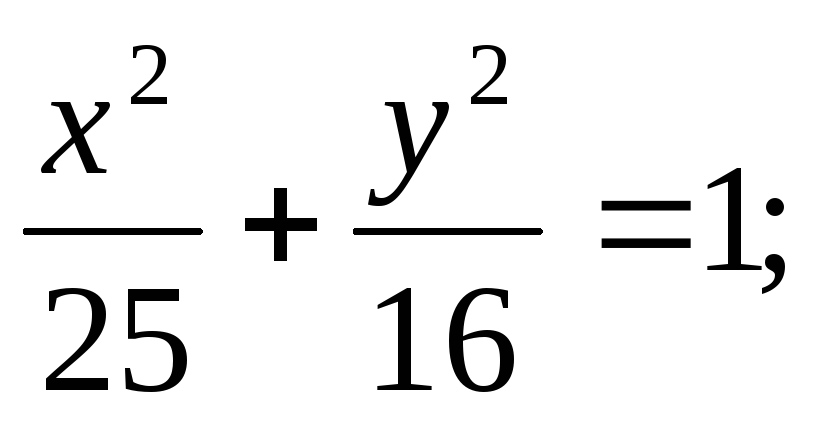 в)
в)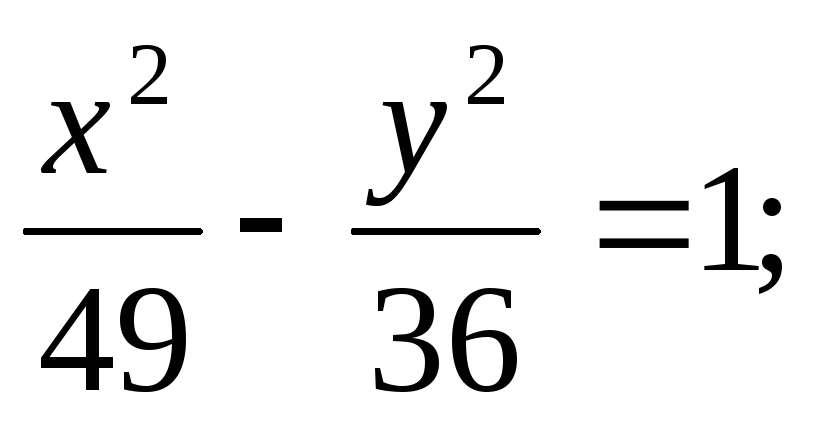 г)
г)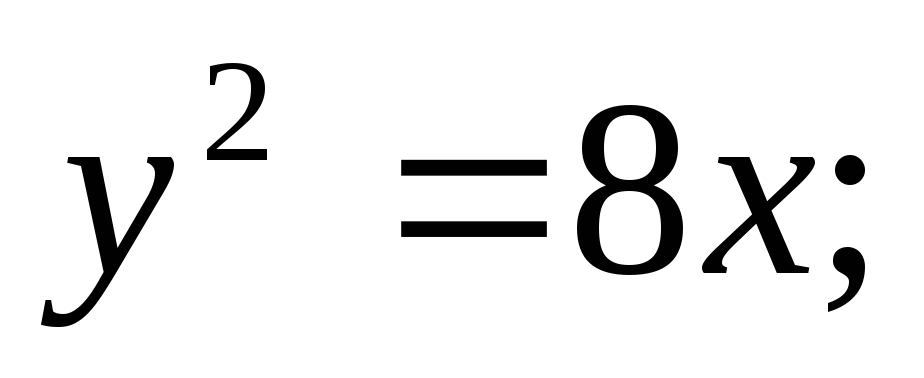
а)
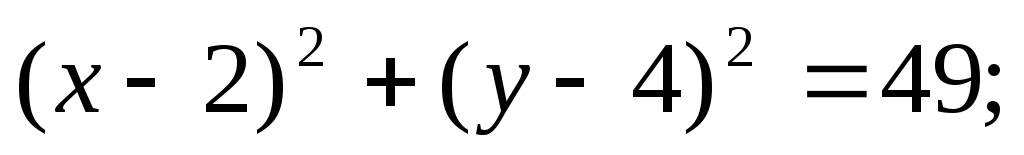 б)
б)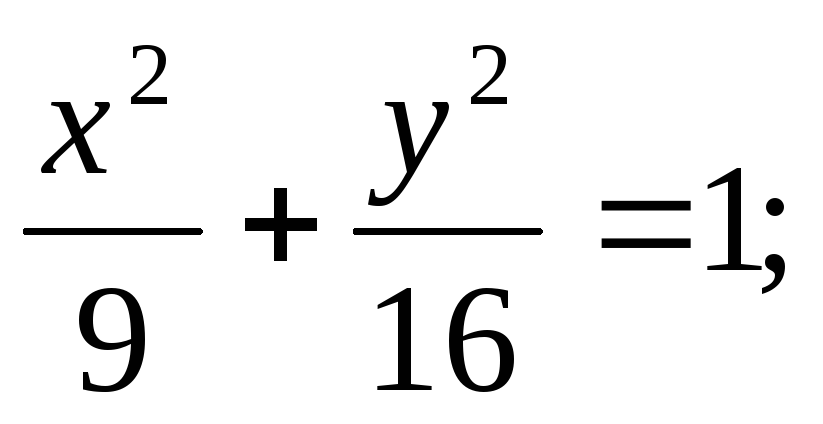 в)
в) г)
г)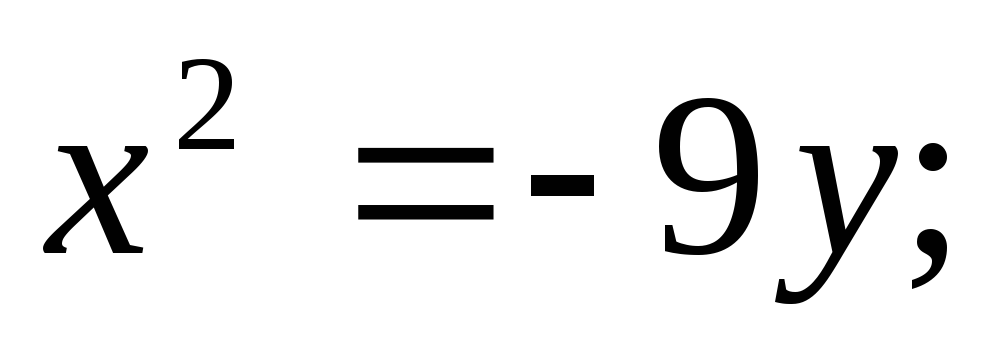
а)
 б)
б)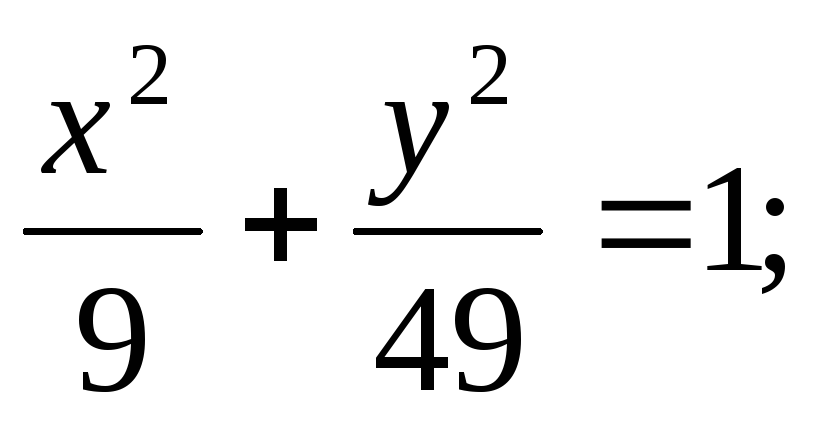 в)
в)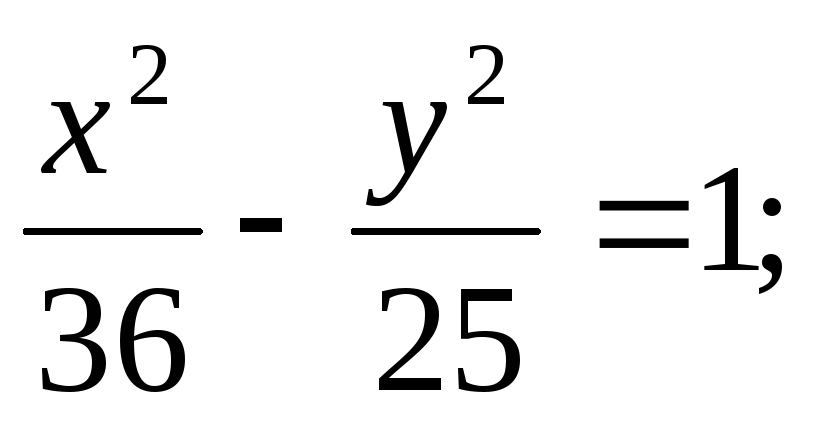 г)
г)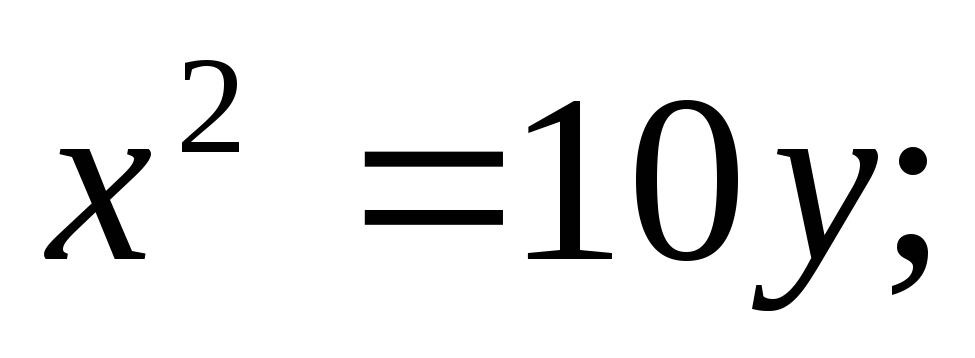
а)
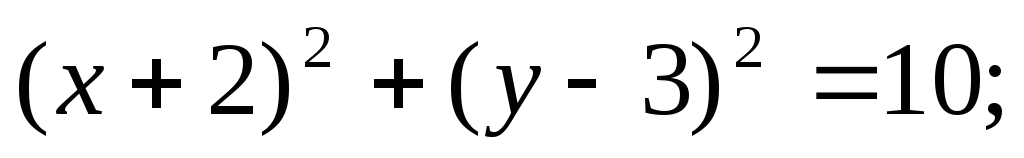 б)
б)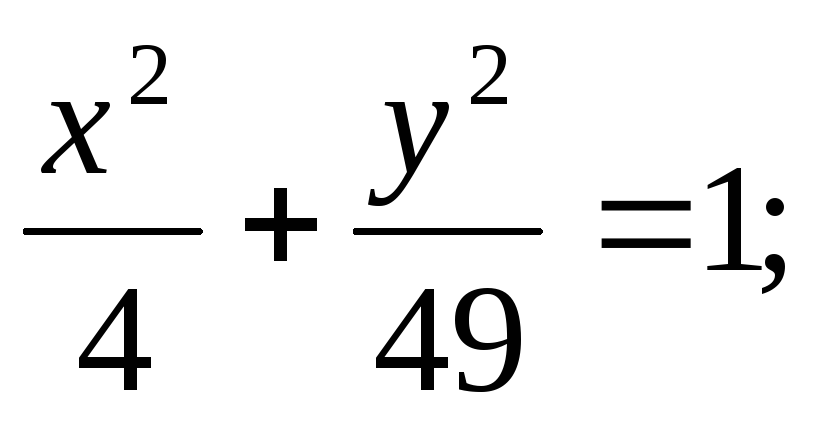 в)
в)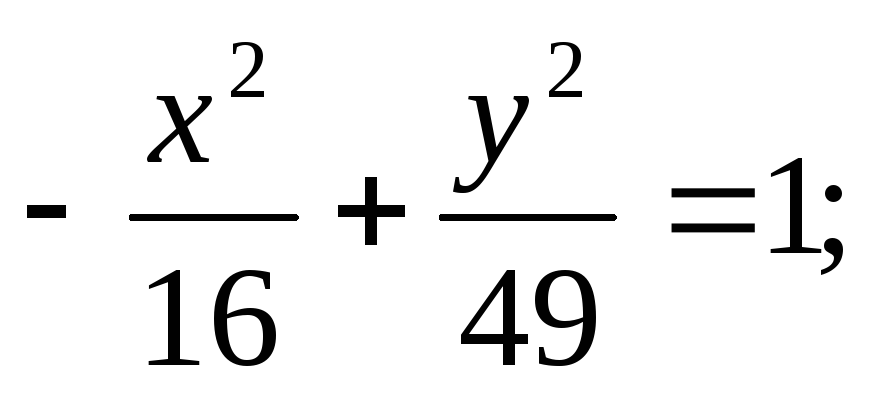 г)
г)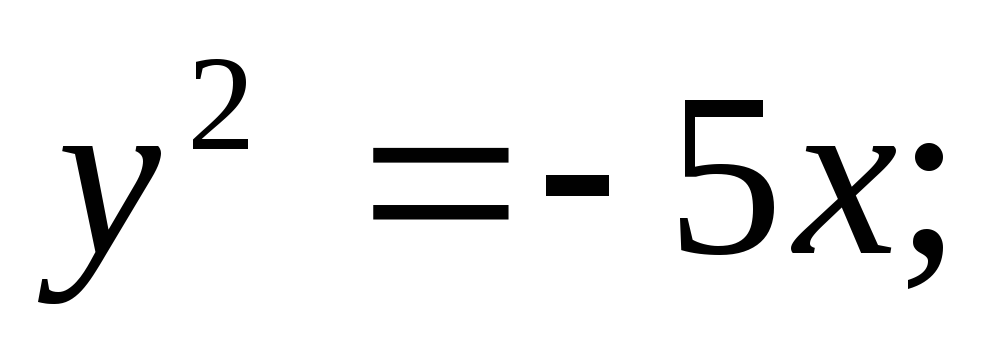
а)
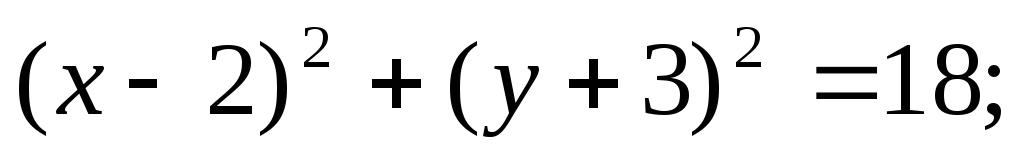 б)
б)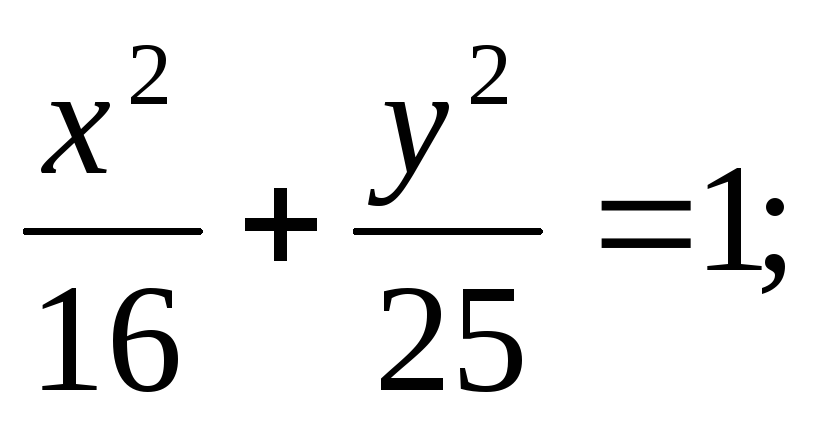 в)
в)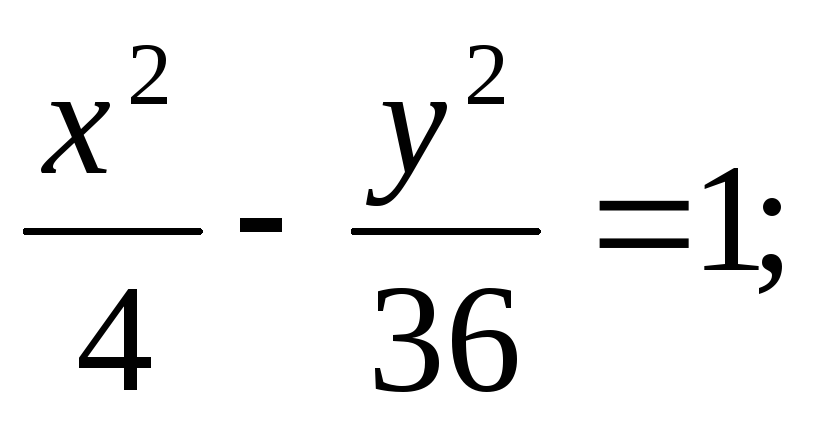 г)
г)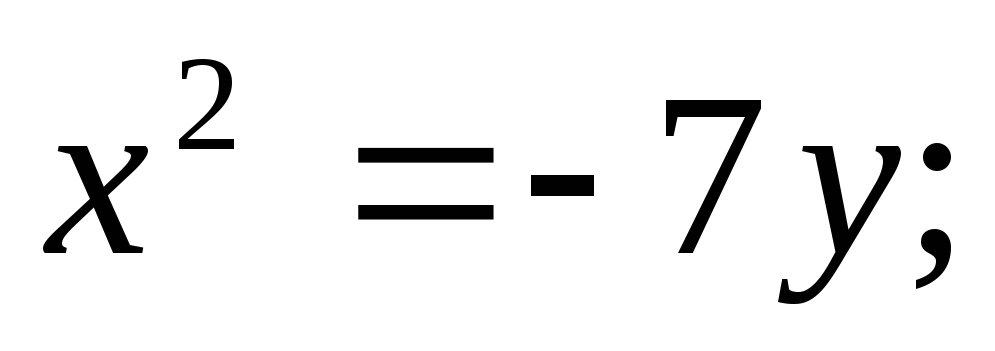
а)
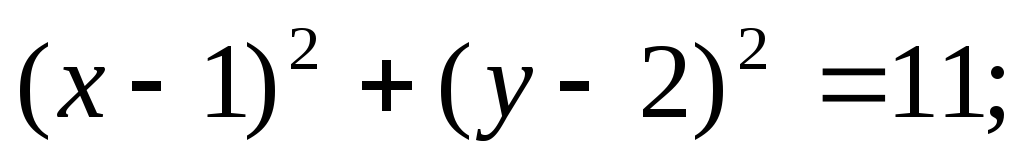 б)
б)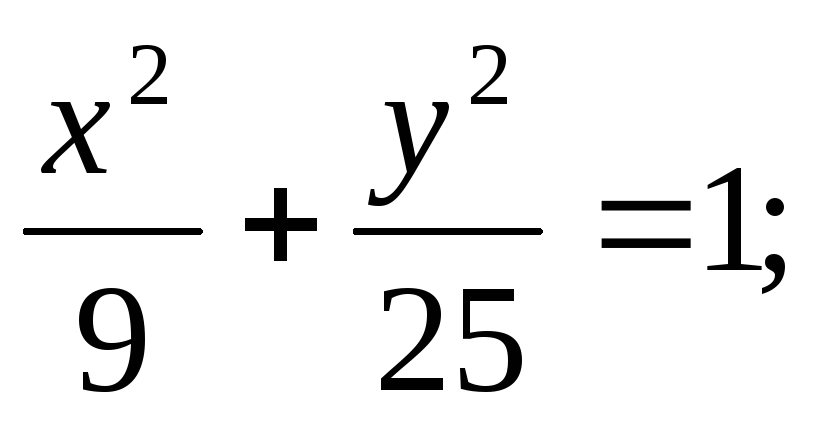 в)
в)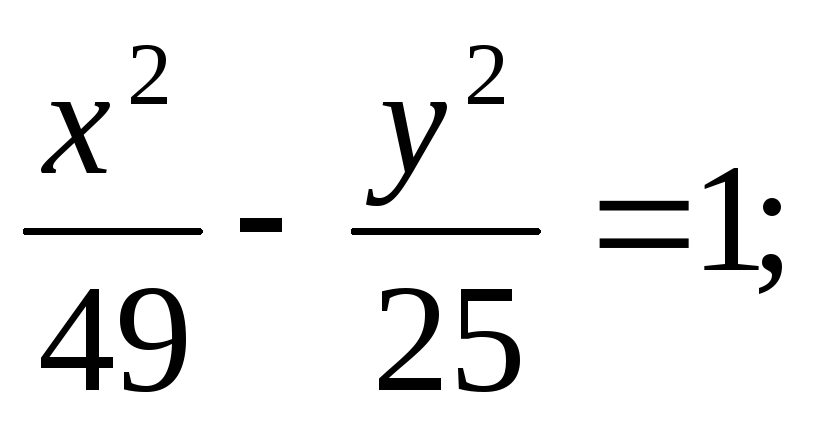 г)
г)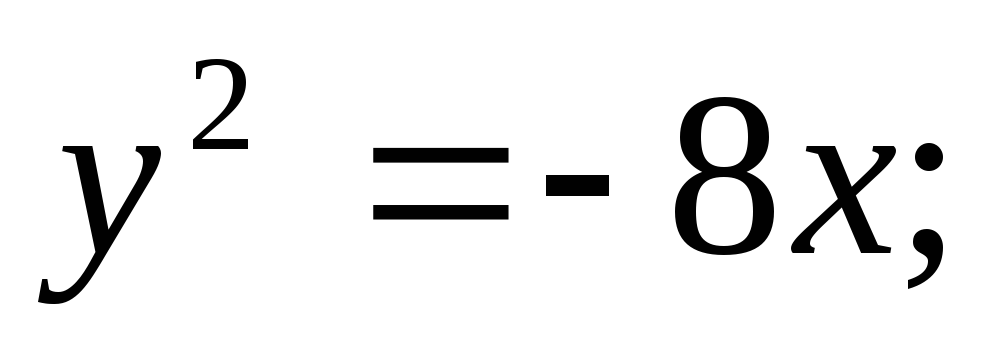
а)
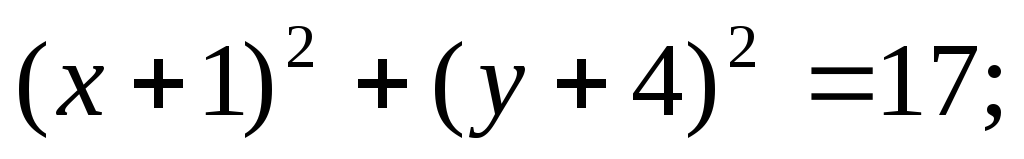 б)
б)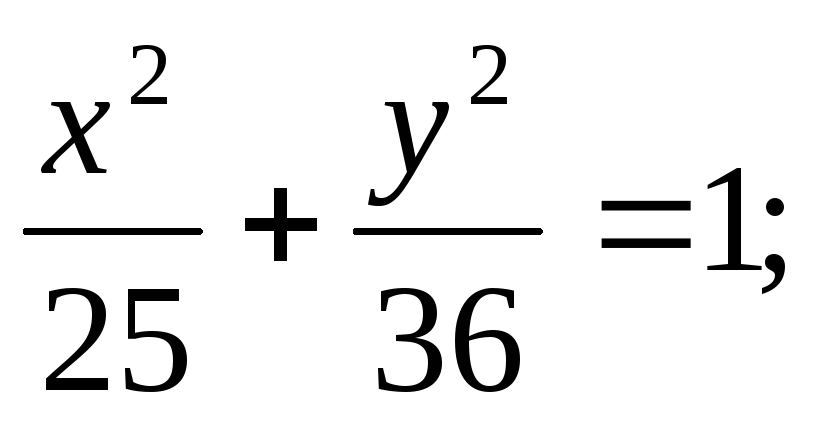 в)
в)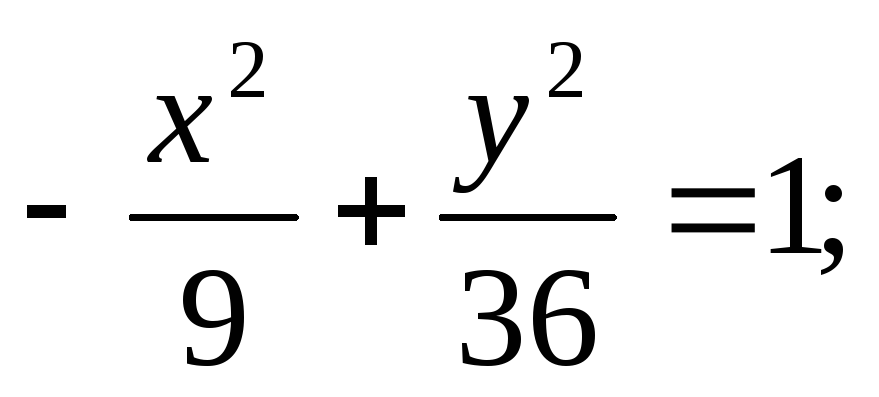 г)
г)