Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Элементы векторной алгебры

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.76 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 224 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Из формулы (4.11.3) следует еще один способ вычисления длины вектора:


	=		2	.	(4.11.4)
a
a		a

Замечание 4.11.2. Формула (4.11.4) применяется в случае гео- метрического способа задания вектора.

4.12. Скалярное произведение в координатах

ТЕОРЕМА 4.12.1. Пусть в ДПСК a = (аx , аy , аz ) , b = (bx ,by ,bz ) .

= axbx+ayby+azbz.

Тогда

Доказательство. По условию

= аx

+ ay

+ az

;

= bx

+ by

+ bz

= (аx

+ ay

+ az

)×(bx

+ by

+ bz

Вычислим

Воспользуемся алгебраическими и геометрическими свойствами

скалярного произведения, при этом будем иметь

аxbx( i × i ) + axby( i × j ) + axbz( i × k ) + aybx( j × i ) + ayby( j × j ) +

+ aybz( j × k ) + azbx( k × i ) + azby( k × j ) + azbz( k × k ) = axbx + ayby + azbz,

что и требовалось доказать.

Замечание. Условие перпендикулярности в координатной форме

a^ b Û axbx +ayby+azbz = 0.

4.13.Приложения скалярного произведения

Геометрические приложения

Проверка перпендикулярности векторов:

= 0 или

axb +ayby+azbz = 0.

Вычисление угла между векторами:

× cos(

), то

Так как

cos (

) =

cos (

) =

a xbx + a yb y + a zbz

a x2 + a 2y + a z2 × bx2 + by2 + bz2

Нахождение проекции вектора на вектор:

a ×b

Так как a ×b = а × прa b пр a b = в координатах a

прa b = a xbx + a yby + a zbz .

a x2 + a 2y + a z2

Неравенство Коши:

Так как a ×b = a × b × cos (a , b ) и cos(a , b ) £1, то

a ×b £ a b a xbx + a yb y + a zbz £ a x2 + a 2y + a z2 × bx2 + by2 + bz2 .

Физические приложения

Вычисление работы силы, действующей при прямолинейном пе- ремещении:

Пусть материальная точка перемещается прямолинейно из точки О в точку А под действием силы F . Тогда, если вектор S = OA – перемеще-

ние материальной точки, а угол между векторами F и S равен a, то рабо- та А, которую совершает эта сила, находится по формуле:

A = F × S × cos a = F × S ,

т.е. работа А равна скалярному произведению силы на вектор перемещения.

Вычисление работы равнодействующей силы:

A = (F1 + F2 + ... + Fn )× S .

4.14. Векторное произведение векторов

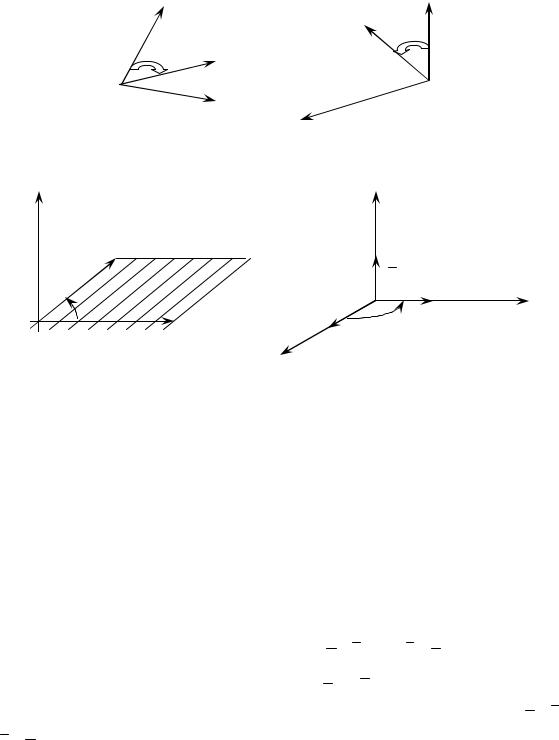
Определение 4.14.1. Упорядоченная тройка некомпланарных век- торов называется правой, если при наблюдении с конца третьего вектора на плоскость, определяемую первыми двумя векторами, кратчайший пово- рот от первого вектора ко второму совершается против часовой стрелки (в положительном направлении) и левой, если этот поворот совершается по часовой стрелке (в отрицательном направлении) (рис. 11).

Определение 4.14.2. Векторным произведением векторов a и b

называется вектор c , удовлетворяющий следующим условиям (рис. 12):

, т.е.

^ плоскости векторов

;

упорядоченная тройка векторов (

) – правая;

sin (

левая

правая

Рис. 11

					k
b					k
b
	α
				i
				i		j	y
						j	y
			x
		a
			Рис. 12
Замечание 4.14.1.			Первые два условия определяют направление

вектора векторного произведения, третье условие – длину вектора вектор- ного произведения. Обозначают векторное произведение следующим обра-

= c .

зом: с = a ´ b или a ,b

Алгебраические свойства векторного произведения

ТЕОРЕМА 4.14.1. Векторное произведение антикоммутативно, т.е.

		´	b	= -	b	´		.	(4.14.1)
	a						a

Доказательство. Так как векторы a ´ b и -(b ´ a ) перпендикуляр-

ны плоскости, проходящей через векторы a и b , то оба эти вектора лежат на одной прямой, т.е. являются коллинеарными. Кроме того, a ´ b и

-(b ´ a ) имеют по определению одинаковые модули (площадь параллело-

грамма остается неизменной).

Тройка векторов ( a , b , a ´ b ) является правой, тройка векторов

( a , b , b ´ a ) - левой. Следовательно, векторы a ´ b и -(b ´ a ) направлены противоположно. Тогда a ´ b = -(b ´ a ) , что и требовалось доказать.

ТЕОРЕМА 4.14.2. Для любого l Î R и для любых векторов a и b справедливы равенства

) ´

´ ( l

)=l(

(4.14.2)

Другими словами, векторное произведение ассоциативно относи- тельно скалярного множителя.

ТЕОРЕМА 4.14.3. Векторное произведение обладает распреде-

лительным свойством:

1)a ´ (b + c ) = a ´ b + a ´ c ;

2)(a + b)´ c = a ´ c + b ´ c .

Упражнение. Теоремы 4.14.2 и 4.14.3 доказать самостоятельно. Замечание 4.14.1. Из алгебраических свойств векторного про- изведения следует, что с векторным произведением можно поступать как с умножением многочленов, учитывая при этом свойство антикомму-

тативности.

Геометрические свойства векторного произведения

ТЕОРЕМА 4.14.4.

Доказательство.

Необходимость.

являются колли-

Пусть векторы

неарными. Покажем, что векторное произведение равно нуль-вектору. Действительно, т.к. векторы a и b являются коллинеарными, то угол a

между этими векторами равен нулю либо 1800 . В этом случае sin a = 0 , а,

следовательно, a ´ b = 0 a ´ b = 0 .

Достаточность.

= 0 . Покажем, что векторы

Пусть

являются коллинеарными. Если какой-либо из векторов

– нулевой,

то он являются коллинеарным любому вектору. Если

¹ 0

¹ 0 , тогда

= 0 следует, что

×sin a = 0 , но тогда равенство воз-

из

можно только при условии, что sin a = 0 , что и означает коллинеарность векторов a и b .

Следствие.

Из Т.14.4

следует, что

(векторный квад-

рат вектора равен нуль-вектору).

ТЕОРЕМА 4.14.5.

S параллелограмма =

Модуль векторного произведения числен-

но равен площади параллелограмма, построен-

ного на векторах

и b (рис. 13).

Рис. 13

ТЕОРЕМА 4.14.6.

Пример. Найти векторное произведение векторов ортонормиро-

ванного базиса (рис. 14).

По свойству коллинеарности векторов имеем:

0, k ´ k = 0 .

. Для вектор-

Рассмотрим векторные произведения

имеем, что па-

ного произведения i

раллелограмм,

построенный на векто-

рах

– квадрат

со стороной, рав-

ной единице. Значит, площадь квадрата

равна единице. Вектор

перпенди-

кулярен векторам i

j , образует с

ними правую тройку, и, следовательно,

есть еди-

векторное произведение

Рис. 14

ничный вектор, направленный по оси

Oz вверх, т.е.

Аналогичным образом находим, что

По Т.4.14.1 (свойства антикоммутативности

векторного

произведения)

имеем:

= -

Замечание 4.14.2.

Векторное

произве-

j -

+ k

дение векторов

можно определить и по

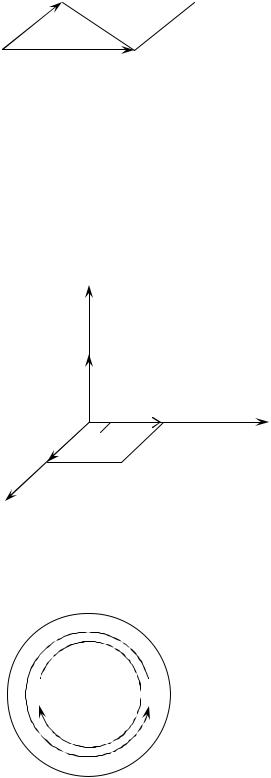
следующей схеме (рис. 15).

Векторное произведение двух любых смеж-

Рис. 15

ных векторов на окружности есть следующий век-

тор со знаком «+», если направление движения

совпадает с положительным направлением (против хода часовой стрелки), и «–», если движение совпадает с отрицательным направлением (по ходу часовой стрелки).

4.15. Векторное произведение в координатах

ТЕОРЕМА 4.15.1. Если векторы a и b заданы в ортонормиро- ванном базисе, то координаты их векторного произведения в том же базисе можно получить, раскрыв символический определитель:


i		j	k
a x		a y	a z	(4.15.1)
	bx	by	bz

Доказательство. Пусть a =ax i +аy j +az k ; b =bx i +by j +bz k . Ум-

ножим векторы a и b векторным образом, раскрывая скобки по алгебраи- ческим свойствам (Т.4.14.1, Т.4.14.2), а также, используя результаты век- торного умножения векторов ортонормированного базиса. Будем иметь:

a × b = (ax i +аy j +az k )×( bx i +by j +bz k )= a xbx i × i + a xby i × j + + a xbz i × k + a ybx j × i + a yby j × j + a ybz j × k + a zbxk × i + + a zb yk × j + a zbz k × k = i (a ybz − a zby ) − j (a xbz − a zbx ) + + k (a xby − a ybx ).

Полученную формулу векторного произведения векторов a и b в координатной форме можно записать в символической формуле:

a y

a z

a x

a y

× b = i

− j

+ k

a x

a y

a z

4.16.Приложения векторного произведения

Геометрические приложения

1.Проверка коллинеарности двух векторов:

a || b a × b = 0 .

2. Определение площади параллелограмма:

Sпараллелограмма = a × b ,

модуль векторного произведения векторов a и b равен площади паралле- лограмма, построенного на этих векторах.

3. Определение площади треугольника:

S= 1 a ´ b , 2

площадь треугольника составляет половину площади параллелограмма,

построенного на векторах a и b .

Физические приложения

1. Момент силы

Определение 4.16.1. Пусть тело закреплено в точке А. В некоторой

точке В этого тела пусть приложена сила F . Моментом силы F отно-

сительно точки А называют вектор равный: AB ´ F .

Приняты обозначения: mom A

M A

´ F

Задача.

Даны точки А(2;1; 3); В(0;1; 3)

и сила

(0; 4; 3). Вы-

числить momB F

Решение.

Вычислим

= (2, 0, 0). Воспользуемся определением

момента силы и вычислим его по формуле 4.15.1:

momB F

= BA ´ F =

Способ 1.=

(0 ×3 - 0 × 4) -

(2 ×3 - 0 × 0) +

(2 × 4 - 0 × 0) =

= i ×0 - j ×6 + k 8 = -6 j + 8 k .


	i		j	k
Способ 2. =	i		j	k	= -2	i	k		= -6		+ 8			.

	2	0		0						j			k
	0	4		3		4	3
	0	4		3
Таким образом, координаты вектора
												= (0, -6, 8).
								momB F				= (0, -6, 8).

2. Линейная скорость вращения

Пусть М точка твердого тела вращается с угловой скоростью ω во-

круг неподвижной оси, тогда скорость u точки М определяется форму-

лой u = w´ r , где r = OM , О – некоторая неподвижная точка оси l.

4.17. Смешанное произведение векторов

Три вектора можно перемножить – 1)

- вектор,

- число,

- вектор.

Определение 4.17.1. Смешанным или векторно-скалярным про-

изведением упорядоченной тройки векторов называется скалярное произ- ведение одного из этих векторов на векторное произведение двух других. abc = a ×b ´ c . .

Замечание 4.17.1. Смешанное произведение представляет собой некоторое число.

Геометрические свойства смешанного произведения

ТЕОРЕМА 4.17.1. Смешанное произведение трех некомпланар- ных векторов равно объему параллелепипеда, построенного на этих век- торах, взятому со знаком «+», если эти векторы образуют правую тройку, и со знаком «-», если они образуют левую тройку.

Упражнение. Теорему 4.17.1 доказать самостоятельно.

ТЕОРЕМА 4.17.2. Смешанное произведение трех ненулевых век-

торов a,b ,c равно нулю тогда и только тогда, когда они компланарны.

Доказательство. ) Предположим противное: пусть a ´ b × c = 0 и

векторы a,b ,c не являются компланарными. Тогда на них можно постро-

ить параллелепипед с объемом V ¹ 0 . Но по Т. 4.17.1 a ´ b × c = ±V , откуда

¹ 0 , что противоречит предположению. Значит,

ком-

имеем

планарны.

Ü) Пусть векторы

компланарны. Тогда вектор

будет

перпендикулярен плоскости, в которой лежат векторы

и, следова-

тельно, вектор a ´ b перпендикулярен вектору c . Значит, из свойств ска- лярного произведения, будем иметь a ´ b × c = 0 , что и требовалось доказать.

Алгебраические свойства смешанного произведения

ТЕОРЕМА 4.17.3. Смешанное произведение не меняется при циклической перестановке его сомножителей:

a ´ b × c = b ´ c × a = c ´ a ×b .

Доказательство. Верность равенства следует из того, что в этом случае не изменяется ни объем параллелепипеда, ни ориентация, соответ- ствующих ребрам, векторов.

ТЕОРЕМА 4.17.4. Смешанное произведение не меняется при пе- ремене местами знаков векторного и скалярного умножения:

a ´ b × c = a ×b ´ c .

Доказательство. Из геометрического смысла смешанного произ-

ведения следует, что a ´ b × c = ±V и a ×b ´ c = b ´ c × a = ±V . Знаки в правых

частях равенств совпадают, т.к. тройки векторов a,b ,c и b,c , a имеют

одинаковую ориентацию. Значит,

Замечание 4.17.2.

Результат, полученный в Т.4.17.4, позволяет

записывать смешанное произведение упорядоченной тройки

векторов

в виде

abc (без знаков скалярного и векторного произведения).

ТЕОРЕМА 4.17.5.

Смешанное произведение меняет

свой знак

при перемене мест любых двух векторов-сомножителей:

= -

= -ba

= -

abc

Упражнение.

Доказать Т.4.17.5 самостоятельно.

4.18. Смешанное произведение в координатах

ТЕОРЕМА 1.18.1. Пусть упорядоченная тройка векторов a,b ,c задана в ортонормированном базисе. Тогда смешанное произведение этих векторов может быть определено по формуле:

a x

a y

a z

c x

c y

c z

Доказательство.

Вычислим

a x

a y

´ b =

- j

+ k

Тогда по определению

будем иметь:

a x

a y

´ b ×

= c x

- c y

+ c z

. (4.18.1)

a x a y

a z

Разложим далее определитель bx by bz по элементам третьей

c x c y c z

строки:

a x

a y

a z

= c x

a y

a z

- c y

a x

a z

+ c z

a x

a y

. (4.18.2)

c x

c y

c z

Сравнивая полученные равенства (4.18.1) и (4.18.2), придем к формуле

			a x	a y	a z
		=	bx	by	bz	, что и требовалось доказать.
a	bc	=	bx	by	bz	, что и требовалось доказать.
			c x	c y	c z

4.19.Приложения смешанного произведения

1.Вычисление объемов параллелепипеда и пирамиды

Vпар.=

Vпирам =

2. Изучение возможного расположения трех векторов

1)a b c = 0 компланарны (линейно зависимы);

2)a b c > 0 не компланарны (линейно независимы), образуют правую тройку;

3)a b c < 0 не компланарны (линейно независимы), образуют левую тройку.

3. Изучение принадлежности четырех точек плоскости

Пусть А(x1, y1, z1); B (x2, y2, z2); С (x3, y3,

z3); D (x4, y4, z4).

Точки будут принадлежать плоскости то-

гда и только тогда, когда векторы

= 0 . Из

будут компланарны

по-

следнего равенства имеем условие принадлеж-

ности четырех точек одной плоскости (рис. 16):

Рис. 16

<<< < Предыдущая 1 2 34 / 224 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб45умк_Цывис_Функции_Интеграл. исчисл..pdf