14-es_1 / Высшая математика (РТФ) / умк_Вакульчик_Элементы векторной алгебры

Определение 5.6.2. Ось, на которой находятся вершины гипербо- лы называется действительной. Ось, на которой нет вершин, называется

мнимой.

Важные характеристики гиперболы

5.x = ± ae - уравнения директрис.

6.e = r , где r - расстояние от точки гиперболы до фокуса; d - рас- d

стояние от точки гиперболы до односторонней директрисы.

7.r1 = ex - a - фокальные радиусы правой ветви гиперболы; r2 = ex + a

центр симметрии в точке C ( x0 , y0 ) .

5.7. Парабола. Каноническое уравнение параболы

Определение 5.7.1. Параболой называется геометрическое место точек плоскости, равноудаленных от фиксированной точки плоскости (фо- куса) и данной прямой (директрисы), лежащей в этой же плоскости.

Расстояние между фокусом и директрисой принято обозначать p . Пусть M (x, y) - произвольная точка параболы. Соединим точку М с

F. Проведём отрезок MN перпендикулярно директрисе. Согласно опреде-

121

быть выведено аналитическими средствами. Его форма зависит от того, в какой части плоскости находится фокус.

1. Пусть фокус F находится в правой полуплоскости, на оси Ox, а вершина параболы в начале координат, тогда каноническое уравнение вы- глядит следующим образом:

y 2 = 2 px .

параболе.

122

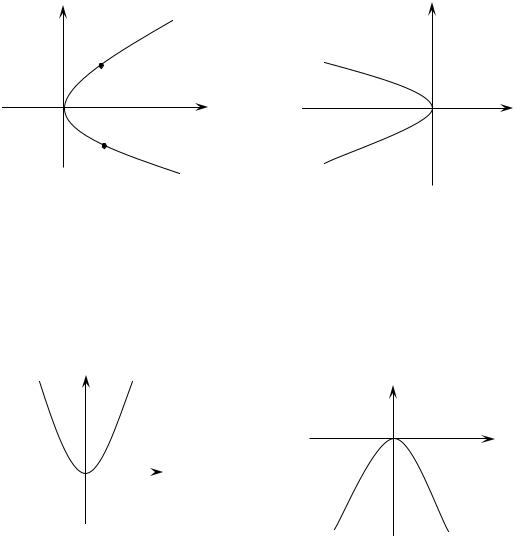
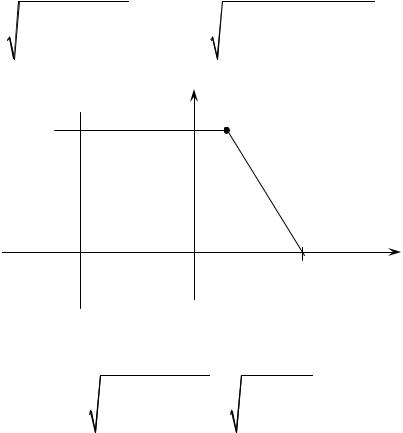
2. Каноническое уравнение параболы, расположенной в левой полу- плоскости (рис. 14), выглядит следующим образом: y 2 = −2 px .

Каноническое уравнение параболы, расположенной в верхней полу-

Оx

болу, вершина которой имеет координаты A( x0 ; y0 ) .

123

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

ВПРОСТРАНСТВЕ

ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

5.8.Определение функции нескольких переменных. Поверхность в пространстве. Алгебраические поверхности

Функция одной переменной не охватывает все зависимости, сущест- вующие в природе. Например, из физики известно, что объём газов по за-

R − const, T − температура, ρ − давление. Очевидно, что V газа зависит от двух переменных величин: ρ и T .

На практике приходится рассматривать объекты с более сложными зависимостями. Следовательно, необходимы новые средства математики для описания таких объектов.

Определение 5.8.1. Переменная величина y называется функцией нескольких переменных, если каждой упорядоченной n-ке чисел соответ- ствует единственное определенное значение y .

Обозначают: y = f ( x1, x2 ,..., xn ). Чаще всего мы будем рассматри- вать функции двух или трёх переменных: z = f ( x, y ); u = f ( x, y, z ) .

Определение 5.8.2. Графиком функции z = f ( x, y ) называется множество точек реального пространства с координатами M ( x, y, f ( x, y )).

Определение 5.8.3. Если в пространстве введена фиксированная система координат (например, ДПСК), то функция z = f ( x, y ) задает неко-

торую поверхность в пространстве.

Определение 5.8.4. Уравнением поверхности в фиксированной системе координат называется такое уравнение с тремя переменными F (x, y, z) = 0 , которому удовлетворяют координаты точек поверхности и

только они.

Определение 5.8.5. Если уравнение поверхности в ДПСК в про- странстве задаётся в виде F (x, y, z) = 0 , где F − многочлен n-ой степени от- носительно x, y, z, то говорят, что задана алгебраическая поверхность n-

го порядка.

124

Ax + By + Cz + (− Ax0 − By0 − Cz0 ) = 0 получим общее уравнение плоскости.

Определение 5.9.3. Уравнение (5.9.1) называется общим уравне- нием плоскости, проходящей через точку M 0 , перпендикулярно вектору n .

Задача 2 (уравнение плоскости в отрезках). Написать уравнение плоскости, если известны величины отрезков, отсекаемых плоскостью на осях координат: a,b,c (рис. 19).

Общее уравнение искомой плоскости имеет вид (*). По условию

126

Задача 4 (уравнение плоскости, проходящей через две точки, па-

раллельно вектору). Написать уравнение плоскости, проходящей через точки M 1 ( x1, y1, z1 ) , M 2 ( x2 , y2 , z2 ) и параллельной вектору а(a x , a y , a z ) .

Решение. Задача имеет смысл, если вектор M 1M 2 не параллелен a

(рис. 22).

1 способ. Возьмём произвольную точку M ( x, y, z ). Тогда

M Îa Û M 1M × M 1M 2 × a = 0 Û

– уравнение плоскости, проходящее через две точки, параллельно данному вектору.

2 способ.

1)М1

2)n = M 1M 2 ´ a .

Задача 5 (уравнение плоскости, проходящей через точку парал-

лельно заданным двум векторам).

Написать уравнение плоскости, проходящей через точку M 1 ( x1, y1, z1 ) ,

параллельно двум векторам а(a x , a y , a z ) , b (bx ,by ,bz ) (рис. 23).

Решить самостоятельно.

128

5.10. Расстояние от точки до плоскости

Пусть заданы точка M 1 ( x1, y1, z1 ) и плоскость α : Ax+By+Cz+D=0. Аналогично, как и для прямой, выводится формула

d (M 1,a) = Ax1 + By1 + Cz1 + D . A2 + B 2 + C 2

Вывести самостоятельно.

5.11. Угол между плоскостями

Определение 5.11.1. За угол между двумя плоскостями принима- ется величина одного из смежных двухгранных углов, образованных при их пересечении.

5.12. Взаимное расположение плоскостей

Пусть заданы общие уравнения двух плоскостей: α1 : A1x + B1 y + C1z + D1 = 0,

3)n1 n2 A1A2 + B1B2 + C1C2 = 0 α1 α 2 ;

4)n1 не параллелен n2 Û a1 Ç a 2 = {L} .

129

ПРЯМАЯ В ПРОСТРАНСТВЕ

5.13.Задание прямой общими уравнениями

Линию в пространстве можно рассматривать, как пересечение двух поверхностей. В частности, прямую в пространстве (алгебраическая линия 1-го порядка) можно задать пересечением двух плоскостей. Следовательно, аналитически прямая будет задаваться системой двух линейных уравнений:

Определение 5.13.1. Формулы (5.13.1) называются общими урав- нениями прямой в пространстве.

Замечание. Плоскости пересекаются по прямой тогда и только тогда, когда они не параллельны. Значит, система уравнений (5.13.1) будет задавать прямую, когда n1 не параллелен n2 .

5.14. Канонические уравнения прямой, проходящей через точку, параллельно данному вектору

циональности в (5.14.1) будет иметь своё определённое значение. Если обозначить его t R , то получим параметрические уравнения прямой: