умк_Вакульчик_Элементы векторной алгебры

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ответ: а) sin (P, L) =

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.76 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2217 18 19 20 21 22 > Следующая >>>

7. Студенты самостоятельно решают задачу:

ЗАДАЧА. Установить, что каждое из следующих уравнений опре- деляет параболу, найти координаты ее вершины А и величину параметра р:

а) y	2 = 4x − 8 ;	б) y = −	1	x	2	+ 2x − 7 ;	в) x = 2 y 2	−12 y + 14 .
		б) y = −	6	x		+ 2x − 7 ;
			6

Ответ: а) A(2;0) , p = 2 .

б) A(6;−1) , p = 3 .

в) А(-4; 3), p = 1 . 4

Замечание. У всех студентов, работающих у доски, проверяет- ся знание таблицы производных, правил дифференцирования.

Домашнее задание

1.Подготовка теоретического материала по теме «Уравнение по- верхности в пространстве. Плоскость как поверхность 1-го порядка. Урав- нение плоскости по точке и нормальному вектору, в «отрезках», по трем точкам. Угол между плоскостями. Расстояние от точки до плоскости».

2.Составить уравнение эллипса, зная, что:

а)	его большая полуось равна 10 и	фокусы				имеют				координаты
F1 (−6;0) , F2 (10;0) ;
б) a = 5 , F1 (−3;5), F2 (3;5).
	( x − 2)2		y	2			x	2		( y − 5)2
	Ответ: 1)	+			= 1;	2)			+	= 1.
	Ответ: 1)	+	36		= 1;	2)			+	= 1.
	100		36			25				16
3.	Установить, что уравнение 16x 2 − 9 y 2 − 64x −18 y + 199 = 0 опре-

деляет гиперболу. Найти ее центр, полуоси, эксцентриситет, уравнения асимптот и директрис.

Ответ: C (2;−1) , a = 3 , b = 4 , ε = 5 , 4

уравнения асимптот: 4x + 3y − 5 = 0 и 4x − 3y −11 = 0 , уравнения директрис: y = −4, 2 и y = 2,2 .

4. Установить, что каждое из следующих уравнений определяет па- раболу. Найти координаты ее вершины А и величину параметра р.

а) y = 4x 2 − 8x + 7 ;	б) x = −	1		y 2 + y .

	4
	Ответ: а) A(1;3) , p =		1		, б) A(1;2) , p = 2 .

	8

161

IV. Уравнение поверхности в пространстве. Плоскость как поверхность 1-го порядка. Уравнение плоскости по точке и нормальному вектору, в «отрезках», по трем точкам. Угол меж- ду плоскостями. Расстояние от точки до плоскости

1. Краткий теоретический обзор с использованием лекционного ма- териала, графической схемы, информационной таблицы. Основной акцент ставится на усвоение способов задания плоскости в пространстве, изуче- ние взаимного расположения плоскостей. Провести краткий анализ реше- ния обучающих задач.

Обучающая задача. Даны четыре точки

A1 (0,7,1) ,

A2 (2, −1,5) , A3 (1,6,3) , A4 (3, −9,8) . Составить уравнения:

а) плоскости A1A2 A3 ,

б) плоскости, проходящей через точку A4 перпендикулярно к векто-

ру A1A2 .

Вычислить косинус угла между координатной плоскостью Oxy и плоскостью A1A2 A3 .

Решение.

а) Воспользуемся уравнением плоскости, проходящей через три точки:

	x - x1				y - y1		z - z1						x - 0 y - 7 z -1
	x - x1				y - y1		z - z1						x - 0 y - 7 z -1
	x2 - x1				y2 - y1		z2 - z1				= 0 ,		2 - 0 -1 - 7 5 -1						= 0 ,
	x3 - x1				y3 - y1		z3 - z1						1 - 0 6 - 7 3 -1
	x y - 7 z -1											x y - 7 z -1						x y - 7 z -1
	x y - 7 z -1											x y - 7 z -1						x y - 7 z -1
	2	-8		4		= 0 ,			2 ×			1	-4		2		= 0 ,	1	-4	2	= 0 ,
	1	-1		2								1 -1			2			1	-1	2
x ×			-4 2		- ( y - 7) ×			1	2	+ ( z -1) ×				1	-4	= 0 ,
x ×			-4 2		- ( y - 7) ×			1	2	+ ( z -1) ×				1	-4	= 0 ,
			-1	2				1	2					1	-1

x ×(-6) - ( y - 7) ×(0) + ( z -1) ×(3) = 0 ,

−6x + 3z − 3 = 0 ,

( A1A2 A3 ): 2x − z + 1 = 0 .

б) a ^ A1A2 n α = ( 1, -4, 2 ) .

162

Воспользуемся формулой:

A( x − x0 ) + B ( y − y0 ) + C ( z − z0 ) = 0 ,

1( x − 3) − 4( y + 9) + 2( z − 8) = 0 , x − 3 − 4 y − 36 + 2z −16 = 0 ,

α : x − 4 y + 2z − 55 = 0 .

Для вычисления угла между плоскостями воспользуемся формулой:

cos (

2 ) =

1 ×

В нашем случае

1 = (0,0,1) ,

2 = (2,0, -1).

Поэтому,

0 × 2 + 0 × 0 +1×(-1)

cos (

2 ) =

-1

= -

12 + 0 2 + 0 2 × 2 2 + 0 2 + (-1)2

1 × 4 +1

2. Студент у доски решает:

−2x + y − z + 1 = 0

Задача 1.

Заданы плоскость Р:

точка

M ( 1;1;1 ) . Написать уравнение плоскости P′ ,

проходящей через точку М,

параллельно плоскости Р, и вычислить расстояние r( P, P′ ) .

Ответ: 2x − y + z − 2 = 0 , r =

Задача 2.

Написать уравнение плоскости P′ ,

проходящей через

заданные точки

M 1 ( 1;2;0 ) и M 2 ( 2;1;1 ) перпендикулярно плоскости Р:

−x + y −1 = 0 .

Ответ: x + y − 3 = 0 .

3.Студент у доски решает:

Задача 1. Написать уравнение плоскости, проходящей через точ- ку M ( 1;1;1 ) параллельно векторам a1 = ( 0;1;2 ) и a2 = ( -1;0;1 ) .

Ответ: x − 2 y + z = 0 .

Задача 2. Написать уравнение плоскости, проходящей через точ- ки M 1 ( 1;2;0 ) и M 2 ( 2;1;1 ) параллельно вектору a = ( 3;0;1 ).

Ответ: −x + 2 y + 3z − 3 = 0 .

4. Студенты самостоятельно выполняют следующее задание: иссле- довать взаимное расположение плоскостей. В случае их параллельности,

163

найти расстояние ρ( P1, P2 ) между плоскостями, а в случае пересечения

плоскостей, найти косинус угла между ними.

а)	P1 : − x + 2 y − z + 1 = 0 ,	P2 : y + 3z −1 = 0 .
б)	P1 : 2x − y + z −1 = 0 ,	P2 : − 4x + 2 y − 2z −1 = 0 .

Ответ а пересекаются ( )

: ) , cos P1, P2

б) параллельны, ρ( P1, P2 ) =

= −			1	.
= −				.
	2		15
	3	.


2	6
2	6

Домашнее задание

1.Подготовка теоретического материала по теме «Прямая в про- странстве, как линия пересечения двух плоскостей. Уравнение прямой в пространстве».

2.Выполнить следующие задания:

Упражнение 1.

Заданы плоскость Р:

x + y − z + 1 = 0

и точка

M ( 3;−2;1 ) . Написать уравнение плоскости

P′ , проходящей через точку

М, параллельно плоскости Р, и вычислить расстояние ρ( P, P′ ) .

Ответ: x + y − z = 0 , ρ =

Упражнение 2.

Написать уравнение плоскости, проходящей через

точку M ( 0;−1;1 ) параллельно векторам

1 = ( 3;1;2 ) и

2 = ( −1;0;1 ) .

Ответ: x − 5 y + z − 6 = 0 .

Упражнение 3.

Написать уравнение плоскости, проходящей через

точки M 1 ( 1;3;0 ) и M 2 ( 2;0;−1 ) параллельно вектору

= ( 2;1;0) .

Ответ: x − 2 y + 7z + 5 = 0 .

Упражнение 4.

Исследовать взаимное расположение

плоскостей.

В случае их параллельности, найти расстояние ρ( P1, P2 ) между плоско-

стями, а в случае пересечения плоскостей, найти косинус угла между ни- ми.

А) P1 :	x − y + 1 = 0 ,	P2 :	y − z + 1 = 0 ;
б) P1 :	2x − y − z + 1 = 0 ,	P2 :	− 4x + 2 y + 2z − 2 = 0 .
				1
		Ответ: а) пересекаются, cos (P1, P2 ) = −			;
		Ответ: а) пересекаются, cos (P1, P2 ) = −		2	;
				2

б) совпадают.

164

V. Прямая в пространстве, как линия пересечения двух плоскостей. Уравнение прямой в пространстве

1.Мини-контрольная по способам задания плоскости.

2.Краткий теоретический обзор с использованием лекционного ма- териала, графической схемы, информационной таблицы. Основной акцент ставится на усвоение способов задания прямой в пространстве, на изуче- ние взаимного расположения прямых в пространстве. Провести краткий анализ решения обучающих задач.

Обучающие задачи

Задача 1. Даны четыре точки A1 (0,7,1) , A2 (2, −1,5) , A3 (1,6,3) ,

A4 (3, −9,8) . Составить уравнения:

а) прямой A1A2 ,

б) прямой A4M , перпендикулярной к плоскости A1A2 A3 , в) прямой A3 N , параллельной прямой A1A2 .

Вычислить синус угла между прямой A1A4 и плоскостью A1A2 A3 .

Решение.

а) Воспользуемся формулой уравнений прямой, проходящей через две точки

x − x1

y − y1

z − z1

x − 0

y − 7

z −1

x2 − x1

y2 − y1

z2 − z1

2 − 0

−1 − 7 5 −1

y − 7

z −1

y − 7

z −1

т.е. A A :

−8

−4

б)

Из

условия

перпендикулярности

прямой

A4M и плоскости

A1A2 A3

следует, что в качестве направляющего вектора прямой можно

взять нормальный вектор

= ( 2,0, −1) плоскости A1A2 A3 . Воспользуемся

формулой

x − x0

y − y0

z − z0

A M :

x − 3

y + 9

z − 8

−1

165

в)

A1A2

|| A3 N , значит, воспользуемся формулой:

x - x0

y - y0

z - z0

= (2 - 0; -1 - 7;5 -1) = (2;-8;4) ||(1;-4;2) .

A1A2

Тогда

A N :

x -1

y - 6

z - 3

-4

= (m, n, p) и

Синус угла между прямой с направляющим вектором

плоскостью с вектором нормали

= ( A, B,C )

вычисляется по формуле:

sin j =

В нашем случае

( A A A ) = ( 2,0, -1 ) ,

S A1A2 = A1A4 = (3 - 0, -9 - 7,8 -1) = (3, -16,7), n × S = 2 ×3 + 0 ×(-16) -1× 7 = 6 - 7 = -1,

n = 2 2 + 0 2 + (-1)2 = 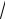4 +1 = 5 ,

S = 32 + (-16)2 + 7 2 = 9 + 256 + 49 = 314 .

Значит,	sin j =		-1	=	1	.
			-1		1


	5	× 314			1570

Задача 2. Исследовать взаимное расположение прямых:

x - 2

y + 4

z - 3

x -1

y - 4

z + 2

-3

-2

Найти расстояние и косинус угла между заданными прямыми.

Решение. По

условию имеем направляющие векторы заданных

прямых

1 (2, -3,0)

2 (3,1, -2) ,

а также точки, принадлежащие этим

прямым,

M 0 (2, -4,3)

и M ′0 (1, 4, -2). Тогда

0 = (-1,8, -5). Исследуем

M 0M ¢

взаимное расположение прямых. Для этого вычислим смешанное произве-

дение				рассматриваемых			трех	векторов:
			2	-3	0
			2	-3	0
		¢ =	3	1	-2	= 29 ¹ 0 прямые скрещиваются.
	S1 S 2 M 0M 0	¢ =	3	1	-2	= 29 ¹ 0 прямые скрещиваются.
			-1	8	-5

166

Расстояние между скрещивающимися прямыми определим по фор-

′

муле d ( L1, L2 ) =

. Векторное произведение

× S 2

2 -3

= 6

+ 4

+11

S 2

;

S 2

36 +16 +121

173 .

-2

Отсюда d ( L , L

) =

. Для определения косинуса

S1 ´ S 2

173

cos j =

угла между прямыми воспользуемся формулой:

S 2

Будем

S 2

иметь

cos j =

182

3. Студент у доски решает:

Упражнение 1. Прямая L задана общими уравнениями. Написать для этой прямой канонические уравнения и уравнения в проекциях.

L : 2x - y + 2z - 3 = 0,

x + 2 y - z -1 = 0.

Ответ:

x - x0

y - y0

z - z0

-3

где M 0 ( x0 ; y0 ; z0 ) –

точка прямой L.

Например, M 0

. Уравнения в проекциях:

4x + 3y - 5 = 0,

; -

5x + 3z - 7 = 0,

5 y - 4z +1 = 0.

Студент у доски решает:

Упражнение 2.

Для

прямых

L :

x + 7

y + 4

z + 3

-2

x - 21

y + 5

z - 2

. Требуется:

-4

-1

а) доказать, что прямые не лежат в одной плоскости, т. е. являются скрещивающимися;

167

б) написать уравнение плоскости, проходящей через прямую L2 па- раллельноL1 ;

в) вычислить расстояние между прямыми;

Ответ: б) 4x + 3y + 12z − 93 = 0 ; в) 13 .

Домашнее задание

1.Подготовка теоретического материала по теме «Взаимное распо- ложение прямой и плоскости».

2.Выполнить следующие задания:

Задание 1.	Прямая L задана общими уравнениями:
	L : x − y + z + 2 = 0,
	x + 2 y − 4z −1 = 0.
Написать канонические уравнения прямой, проходящей через точку
M 0 (1; −3;0) .
	Ответ:	x −1	=		y + 3	=	z	.
	Ответ:		=			=		.
	6			5		4
Задание 2.	Даны четыре точки A1 (2, −3,1), A2 (2, −1,5) ,			A3 (1,0,3),

A4 (3, −5, 4). Составить уравнения:

а) прямой A1A2 ,

б) прямой A4M , перпендикулярной к плоскости A1A2 A3 , в) прямой A3 N , параллельной прямой A1A2 ,

Вычислить синус угла между прямой A1A4 и плоскостью A1A2 A3 .

Ответ: а)

x − 2

y + 3

z −1

;

б)

x − 3

y + 5

z − 4

;

в)

x −1

z − 3

; sin ϕ =

−2

Задание 3. Исследовать взаимное расположение прямых

x − 2

y + 5

z − 3

x − 3

y − 4

−3

−2

Найти угол и расстояние между заданными прямыми.

Ответ: прямые скрещиваются; 1; cos ϕ = − 11 . 5 5

168

VI. Взаимное расположение прямой и плоскости

1.Мини-контрольная по способам задания прямой в пространстве.

2.Краткий теоретический обзор с использованием лекционного ма- териала, графической схемы, информационной таблицы. Основной акцент ставится на изучение взаимного расположения прямой и плоскости в про- странстве.

3.Два студента у доски решают (один – с помощью аудитории и преподавателя, другой – самостоятельно):

Упражнение 1. Заданы прямая	L :	x −1	=	y	=	z + 1	и точка
		2
M (0;1;2) L (проверить!). Требуется:			1		0

а) написать уравнение плоскости,	проходящей через прямую L и

точку М; б) написать уравнение плоскости, проходящей через точку М пер-

пендикулярно прямой L;

в) написать уравнение перпендикуляра, опущенного из точки М на прямую L.

Ответ: а) x − 2 y + z = 0 ,

б) 2x + y −1 = 0 ,

x − 2 y + z = 0,

y −1

z − 2

в) 2x + y −1 = 0,

или

−1

Упражнение 2. Заданы плоскость P : x + y − z + 1 = 0

прямая

L :

x −1

z + 1

, причем L P (проверить!). Требуется:

а)

вычислить

sin (P, L) и координаты точки пересечения прямой и

плоскости;

б) написать уравнение плоскости, проходящей через прямую L пер- пендикулярно к плоскости Р.

б) 3x − y + 2z −1 = 0 .

169

4. Студент у доски решает:

Задача.

Написать уравнение прямой, проходящей

через

точку

M 0 (7;1;0)

параллельно плоскости 2x + 3y − z −15 = 0 и пересекающей

прямую

y −1

z − 3

x − 7

y −1

Ответ:

−28

VII. Поверхности второго порядка

Поверхности в пространстве – это геометрическое место точек, удовлетворяющих какому-либо условию. Прямоугольная система коорди- нат Oxy z в пространстве позволяет установить взаимно однозначное соот- ветствие между точками пространства и тройками чисел x, y и z − их коор- динатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности. Ме- жду поверхностями второго порядка и кривыми второго порядка можно установить связь, а именно практически все кривые второго порядка име- ют свой аналог в составе поверхностей второго порядка.

Проведем классификацию поверхностей второго порядка.

= 1

−

= 0

эллипсоид

конус

−

= 1

однополостный

эллиптический

гиперболоид

цилиндр

170

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2217 18 19 20 21 22 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб45умк_Цывис_Функции_Интеграл. исчисл..pdf