Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Элементы векторной алгебры

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.76 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2216 17 18 19 20 21 22 > Следующая >>>

Основная и дополнительная литература

1.Бугров, Я.С. Элементы линейной алгебры и аналитической гео- метрии / Я.С. Бугров, С.М. Никольский. – М.: Наука, 1980.

2.Гусак, А.А. Справочник по высшей математике / А.А. Гусак, Г.М. Гусак. – Мн.: Навука и тэхника, 1991.

3.Мышкис, А.Д. Лекции по высшей математике / А.Д. Мышкис. –

М.: Наука, 1973.

4.Сборник задач по математике для втузов. Линейная алгебра и осно- вы математического анализа / под ред. А.В. Ефимова и Б.П. Демидовича. –

М.: Наука, 1986.

5.Сборник задач по математике для втузов. Специальные разделы математического анализа / под ред. А.В. Ефимова и Б.П. Демидовича. – М.:

Наука, 1981.

I. Прямая на плоскости как линия 1-го порядка. Уравнение прямой на плоскости по точке и нормальному вектору (направ- ляющему вектору, угловому коэффициенту), по двум точкам, в «отрезках». Расстояние от точки до прямой

1.Краткий теоретический обзор с использованием лекционного ма- териала, графической схемы, информационной таблицы. Основной акцент ставится на усвоение способов задания прямой на плоскости.

2.Вместе со всей аудиторией обсуждение решений обучающих задач.

Обучающая задача. Даны		вершины треугольника АВС:
A(−2, −3) , B (1,6) , C (6,1) (рис. 1). Найти:
а) уравнение стороны АВ;		B
б) уравнение высоты СН;
в) уравнение медианы АМ;		H
г) точку N пересечения ме-		M
дианы АМ и высоты СН;			L
д) уравнение прямой, прохо-		N
дящей через вершину С параллель-	А		C
дящей через вершину С параллель-
но стороне АВ;


е) расстояние от точки С до
прямой АВ.		Рис. 1
		Рис. 1

151

Решение.

а) уравнение прямой, проходящей через две точки

x - x1

y - y1

. Значит,

x2 - x1

y2 - y1

x - (-2)

y - (-3)

x + 2

y + 3

x + 2

y + 3

АВ:

, или

1 - (-2)

6 - (-3)

3x + 6 = y + 3 . Таким образом, окончательно имеем

АВ: 3x − y + 3 = 0 .

б) высота CH AB

AB || СН.

Воспользуемся каноническим

уравнением прямой:

x − x0

y − y0

AB = ( 3 ;−1) =

CH ;

C (6;1).

x − 6

y −1

или −( x − 6) = 3( y −1) ,

или −x + 6 = 3y − 3 . Следова-

−1

тельно, СН:

x + 3y − 9 = 0 .

в) определим координаты М, как середины отрезка ВС.

xM	=	x B + x C		;		y M =			y B + y C			.

			2							2
	1 + 6 6 + 1							7		7
M			;		,	M			;		.
	2
			2				2			2

Теперь по двум известным точкам

А и М составляем уравнение

медианы АМ:

x - (-2)

y - (-3)

x + 2

y + 3

или

x + 2

y + 3

или

- (-2)

(-3)

13( x + 2) =11( y + 3),

или 13x + 26 = 11y + 33 .

Таким образом, АМ:

13x −11y − 7 = 0 .

г) для нахождения координат точки

N пересечения медианы АМ и

высоты СН составляем систему уравнений:

13x -11y - 7 = 0,

13 ×(9 - 3y ) -11y - 7 = 0,

- 9 = 0.

= 9 - 3y.

x + 3y

13 ×(9 - 3y ) -11y - 7 = 0 , 117 − 39 y −11y − 7 = 0 , −50 y + 110 = 0 .

152

= ( 3 ;-1). По точке и


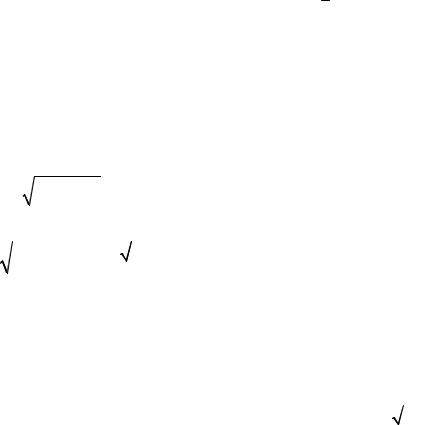
Отсюда, имеем y =	11	;			x = 9 -		33	=	12	.
	5
						5		5
	12			11
Таким образом, N			;			.

5				5

д) так как прямая, проходящая через вершину С, параллельна сторо- не АВ, то за вектор нормали можно взять вектор n AB

нормальному вектору составляем уравнение прямой:

A( x - x0 ) + B ( y - y0 ) = 0 ,

C (6;1).

L: 3( x - 6) -1( y -1) = 0 или 3x −18 − y + 1 = 0 , L: 3x − y −17 = 0 .

е) расстояние от точки С до прямой АВ вычисляем по формуле:

d =

Ax0 + By0

+ C

A2 + B 2

3 × 6 -1 + 3

» 6,3 .

d =

32 + (-1)

Ответ: а) АВ:

3x − y + 3 = 0 ,

б) СН:

x + 3y − 9 = 0 ,

в) АМ: 13x −11y − 7 = 0 ,

12 11

г) N

;

д) 3x − y −17 = 0 ,

е) d =

» 6,3.

3. Два студента у доски параллельно решают по две задачи:

Задача 1.

Прямая L задана точкой M 0 (-1;2)Î L и нормальным

вектором

= ( 2,3 ) . Требуется написать уравнение прямой

L, привести

его к общему виду.

Ответ: L: 2x + 3y − 4 = 0 .

Задача 2.

Написать

уравнение прямой

L1 , проходящей через

точку M 1 ( 2;7 ) , перпендикулярно заданной прямой L: 2x + 3y − 4 = 0 . На- писать уравнение прямой L2 , проходящей через точку M 2 ( - 3;2 ) парал- лельно заданной прямой L.

Ответ: L1 : 3x − 2 y + 8 = 0 , L2 : 2x + 3y = 0 .

153

Задача 3.	Прямая		L задана точкой	M 0 (−1;2) L				и	направ-
ляющим вектором		= ( 3; −1 ) . Записать каноническое и параметрические
ляющим вектором	S	= ( 3; −1 ) . Записать каноническое и параметрические
уравнения прямой L.								x = −1 + 3t,
				x + 1	=	y − 2		x = −1 + 3t,
			Ответ:L:				,		= 2 − t.
			Ответ:L:				,
				3		−1		y
Задача 4.	Прямая		L задана двумя своими точками						M 1 ( 1;2 )

и M 2 ( −1;0 ) . Записать каноническoе и параметрические уравнения пря- мой L.

	x −1	=	y − 2		x = 1 + t,
Ответ:L:				,
Ответ:L:				,
	1		1		y = 2 + t.
4. Студент у доски решает:					A( 1;2 ) ,
Треугольник АВС задан координатами своих вершин					A( 1;2 ) ,

B ( 2;−2 ) и C ( 6; −1 ) . Требуется:

а) Написать уравнение стороны АВ.

Ответ: АВ : 4x + y − 6 = 0 .

б) Написать уравнение высоты CD и вычислить ее длину.

Ответ: СD : x − 4 y −10 = 0 , d = 17 ≈ 4,12 .

в) Найти косинус угла ϕ между высотой СD и медианой ВМ.

Ответ: cos (CD, BM ) =				1	.


		2
5. Студент у доски решает задачу:
Задача. Дана точка M 1 ( 1;2 ) и прямая	L. Вычислить расстояние
от точки M 1 до прямой L. Найти точку M 1′ , симметричную точке M 1 от-
носительно прямой L.
Ответ: d ( M 1, L) =	6		≈ 1,9 , M 1′ (−2,6; 3, 2) .


	10
	10

Домашнее задание

1.Повторение теоретического материала по теме «Прямая на плос- кости». Изучение обучающих задач из следующего практического занятия.

2.Решить следующие задачи:

154

Задача 1.			Прямая L задана точкой M 0 (−2;3) L и нормальным
вектором		= ( 2,3 ) . Требуется написать уравнение прямой							L, привести
	n
его к общему виду.					Ответ: L: 2x + 3y − 5 = 0 .

Задача 2.			Написать уравнение прямой L1 , проходящей через
точку M 1 ( 2;−5 ) ,			перпендикулярно заданной прямой				L: x + 3y − 7 = 0 .
Написать уравнение прямой					L2 , проходящей через точку M 2 ( − 3;1 ), па-
раллельно заданной прямой L.
					Ответ: L1 : 3x − y −11 = 0 ,
							L2 : x + 3y = 0 .
Задача 3.			Прямая		L задана точкой M 0 (−2;3) L						и направ-
ляющим вектором				= ( 0;−1 ) . Записать каноническое и параметрические
			S
уравнения прямой L.											x = −2,
						x + 2	=	y − 3
					Ответ: L:					,	y = 3 − t.
						0		−1
Задача 4.			Прямая L задана двумя своими точками M 1 ( 1;−2 ) и

M 2 ( −1;7) . Записать каноническoе и параметрические уравнения прямой L.

			x −1	=	y + 2			x = 1 − 2t,
		Ответ: L:					,	y = −2 + 9t.
			−2		9
Задание на 9 баллов:
Задача 5.	Даны две	противоположные		вершины квадрата
A( 1;3 ) и C ( −1;1 ) . Найти координаты двух его других вершин и написать
уравнения его сторон.		Ответ: B ( 1;1 ) , D (−1;3) ,

		( AB) : x −1 = 0 , ( BC ) : y −1 = 0 ,
		(CD) : x + 1 = 0 , ( AD): y − 3 = 0 .
Задача 6.	Написать уравнения сторон треугольника							АВС, если
задана его вершина	A( 1;3 ) и	уравнения двух медиан				x − 2 y + 1 = 0 и
y −1 = 0 .
	Ответ: x − y + 2 = 0 , x − 4 y −1 = 0 ,						x + 2 y − 7 = 0 .

155

II. Решение задач на взаимное расположение прямой на плоскости

1.	Мини-контрольная по теме «Производная» (на 5 минут).
2.	Студенты самостоятельно решают:
Даны прямые L :		x -1	=	y + 3	; L		:	x + 2		=	y	. Требуется:
Даны прямые L :			=		; L	2	:			=		. Требуется:
	1	2	-1			2		1		0
		2	-1					1		0
a)	Исследовать взаимное расположение прямых L1 и L2 .
											Ответ: пересекаются.
б)	Найти точку пересечения прямых L1							и L2		, угол между прямыми.
				Ответ: L Ç L						= M ( - 5;0 ) , cos j =			2	.
									2

							1			5
										5

3.Решение и обсуждение задач на 9 баллов из домашнего задания 5 (два студента у доски, пока идет обсуждение первой задачи, второй сту- дент готовит решение второй).

4.Со всей аудиторией анализ решения обучающей задачи.

Обучающая задача. Составить уравнения сторон треуголь- ника, зная одну его вершину C ( 4;3 ) , а также уравнения биссектрисы x + 2 y − 5 = 0 и медианы 4x + 13y −10 = 0 , проведенных из одной вершины.

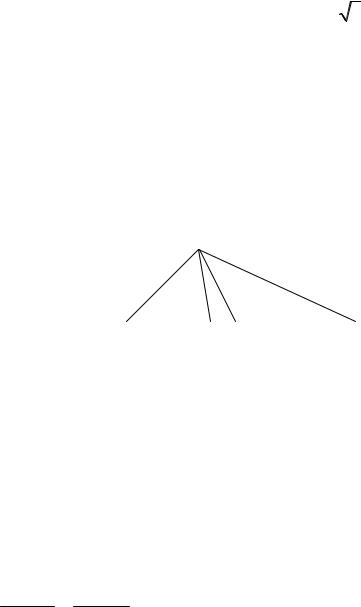
Решение.		Так как точка C ( 4;3 )		B
не принадлежит ни одной из прямых				B
не принадлежит ни одной из прямых
x + 2 y − 5 = 0 и 4x + 13y −10 = 0 ,			то
предположим, что прямые выходят из
вершины	В.	Обозначим	ВК: A	K M	C
x + 2 y − 5 = 0 , ВМ : 4x + 13y −10 = 0 .				Рис. 2
Найдем координаты вершины			В,	Рис. 2
Найдем координаты вершины			В,

как точку пересечения двух прямых. Для этого решим систему уравнений:

B :	x + 2 y - 5 = 0,			x = 5 - 2 y,	x = 5 - 2 y,
	4x +13y -10 = 0		20 - 8 y +13y -10 = 0		5 y = -10
	y = -2,	или B ( 9;	-2 ).
	x = 9

Составим уравнение стороны ВС по двум точкам по формуле:

x - x1 = y - y1 . x2 - x1 y2 - y1

156

BC :	x	− 4	=	y − 3	, или	x − 4	=	y − 3	, или x − 4 = − y + 3 , или
	9					5
		− 4		−2 − 3				−5
BC :	x + y − 7 = 0 .

Так как ВК − биссектриса, то точки, лежащие на прямой ВК равно- удалены от сторон АВ и ВС.

Продолжим биссектрису ВК и проведем через точку С прямую, пер- пендикулярную к ВК (рис. 3).

Так как ВК: x + 2 y − 5 = 0 , то nBK = ( 1;2 ) SCK ′ = ( 1;2 ) , C ( 4;3 ) :


	x − 4	=		y − 3	, или	2x − 8 = y − 3 , или
1		=			, или	2x − 8 = y − 3 , или
1			2
CK′ : 2x − y − 5 = 0 ,
где K′ − точка пересечения биссектрисы ВК и перпендикуляра.
Найдем координаты точки K′ :
	K′ :	x + 2 y − 5 = 0,				x = 5 − 2 y,		x = 5 − 2 y,		y = 1,
	K′ :		2x − y − 5 = 0				= 0.		−5 y = −5.	,	x = 3.

						10 − 4 y − y − 5

Итак, K′( 3;1 ) .

Найдем координаты точки C′ , симметричной точки С, относительно биссектрисы ВК по формулам:

x K ′ =

xC′ + xC

y K ′

yC′ + yC

+ 4

3 =

xC′

xC′ = 6 − 4 ,

xC′ = 2 .

1 =

yC′

+ 3

yC′ = 2 − 3 ,

yC′ = −1.

C′( 2; −1 ) .

C′ AB по построению. По двум точкам находим уравнение прямой

АВ ( B ( 9;−2 ), C′( 2; −1 ) ).

x − 2

y + 1

или

x − 2

y + 1

или

−x + 2 = 7 y + 7 , или

9 − 2

−2 + 1

−1

AB : x + 7 y + 5 = 0 .

Достроим АВС до параллелограмма

ABCM ′ (рис. 4).

Через точку С проведем прямую, параллельную АВ. n AB = ( 1;7 ) , C ( 4;3 ) .

157

	B			B
A
			A	K M	C
	K M	C


	K’
C’					M ¢
					M ¢
	Рис. 3			Рис. 4

Найдем уравнение прямой по точке и перпендикулярному вектору:

A( x − x0 ) + B ( y − y0 ) = 0 .

1( x − 4) + 7( y − 3) = 0 , или x − 4 + 7 y − 21 = 0 , или

CM ′ : x + 7 y - 25 = 0 .

Найдем координаты точки M ′ , где M ′ = BM Ç CM ′ .

4x + 13y −10 = 0,		100 − 28 y + 13y −10 = 0,
M ′ :	= 0.
x + 7 y − 25	= 0.	x = 25 − 7 y.
−15 y = −90,	y = 6,	т.е. M ′(−17;6 ) .
		т.е. M ′(−17;6 ) .
x = 25 − 7 y.	x = −17,

Так как в треугольнике ВМ − медиана, то в параллелограмме BM ′ будет диагональю. Диагонали параллелограмма точкой пересечения делят-

ся пополам. Следовательно, координаты точки

М можно найти,

как сере-

дину отрезка BM ′ .

x B + xM ′

y M

y B + y M ′

9 −17

= −4 ,

y M

= −2 + 6 = 2 .

M ( − 4;2 ).

Точка M AC . По двум точкам можно составить уравнение прямой

АС. M ( − 4;2 ), C ( 4;3 ) .

x + 4

y − 2

или

x + 4

y − 2

или x + 4 = 8 y −16 ,

или

4 + 4 3 − 2

AC : x − 8 y + 20 = 0 .

Ответ: AB : x + 7 y + 5 = 0 ,

BC : x + y − 7 = 0 ,

AC : x − 8 y + 20 = 0 .

4. Мини-диктант по способам задания прямой на плоскости.

158

Домашнее задание

1.Повторить теоретический материал по лекциям и информацион- ной таблице по теме «Линии 2-го порядка на плоскости. Эллипс, гипербо- ла, парабола».

2.Решить:

1) Даны прямые L :	x +1	=	y - 4	;		L		:	x - 2	=	y	. Требуется:
1) Даны прямые L :		=		;		L	2	:		=		. Требуется:
1	-2	0					2	1		5
	-2	0						1		5
а) Исследовать взаимное расположение прямых L1										и L2 .
									Ответ: пересекаются.
б) Найти точку пересечения прямых L1 и L2 , угол между прямыми.
	Ответ: L Ç L					= M ( 2,8; 4 ), cos j = -							1	.
	Ответ: L Ç L				2	= M ( 2,8; 4 ), cos j = -								.
		1			2					26
										26

2) Уравнение одной из сторон угла есть 4x − 3y + 9 = 0 , уравнение его биссектрисы есть x − 7 y + 21 = 0 . Написать уравнение прямой, на кото- рой лежит другая сторона угла.

Ответ: 3x + 4 y −12 = 0 . 3) Треугольник АВС задан координатами своих вершин A(-1; -1 ) ,

B ( 1;3 )	и C ( 4; -1 ) . Из вершины В проведена высота. К какой из сторон
ближе расположена середина этой высоты?
							Ответ: к стороне АВ.
4) Дано уравнение эллипса 24x 2 + 49 y 2 =1176 . Найти:
а)	длины его полуосей;			г)	уравнения				директрис и
б)	координаты фокусов;	расстояние между ними.
в)	эксцентриситет;
	Ответ: а) а=7, b = 2					; б) F1 ( − 5,0) , F2 (5,0 ) ,
	Ответ: а) а=7, b = 2				7	; б) F1 ( − 5,0) , F2 (5,0 ) ,
		в) ε =	5	, г) x = ±			49	, d =	98	= 19,6 .
		в) ε =		, г) x = ±				, d =	5	= 19,6 .
		7			5				5

5) Установить, что уравнение 4x 2 + 3y 2 − 8x + 12 y − 32 = 0 определя- ет эллипс. Найти его центр С, полуоси, эксцентриситет и уравнения ди- ректрис.

Ответ: C (1;−2) , a = 23 , b = 4 , ε = 1 , D1 : y + 10 = 0 , D2 : y − 6 = 0 . 2

159

III. Линии 2-го порядка на плоскости. Эллипс, гипербола, парабола

1.Краткий теоретический обзор с использованием лекционного материала, графической схемы, информационной таблицы, с изображени- ем на доске схематических графиков кривых. Основной акцент ставится на усвоение канонических уравнений трех основных классов невырожденных кривых второго порядка и их построение в декартовой прямоугольной сис- теме координат.

2.Два студента у доски решают упреждающие задачи 4 и 5 из до- машнего задания. Проводится анализ и обсуждение их решений со всей аудиторией.

3.Студенты самостоятельно решают задачу:

Задача. Построить гиперболу 16x 2 − 9 y 2 = −144 . Найти:

а) полуоси;		г) уравнения асимптот;
б) координаты фокусов;		д) уравнения директрис.
в) эксцентриситет;
Ответ: а) а=3, в =4; б) F1 ( 0, −5 ) , F2 ( 0,5 ) ,
в) ε =	5	, г) y = ±	4	x ,	д) y = ±	16	.

4		3			5

4.Преподаватель у доски напоминает методику выделения полного квадрата в квадратном трехчлене.

5.Студент у доски решает задачу:

ЗАДАЧА. Установить,	что	данное	уравнение
9x 2 −16 y 2 + 90x + 32 y − 367 = 0	определяет гиперболу. Найти ее центр С,
полуоси, эксцентриситет, уравнения асимптот и директрис.
	Ответ:	С(-5,1);	а=8, в=6; ε =	5	;

			4

уравнения асимптот: 3x − 4 y + 19 = 0 , 3x + 4 y + 11 = 0 ;

уравнения директрис: x = − 7 , x = 57 . 5 5

6. Студент у доски решает задачу:

ЗАДАЧА. Написать уравнение параболы с вершиной в начале ко- ординат, если известно, что парабола расположена в левой полуплоскости

симметрично относительно оси ОХ и p = 1 . 2

Ответ: y 2 = −x .

160

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2216 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб45умк_Цывис_Функции_Интеграл. исчисл..pdf