Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Элементы векторной алгебры

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

4.76 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2211 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА МОДУЛЯ

			Нагляд
		Номер	ные и	Формы
		Номер	мето-	Формы
	Название вопросов,	практи-	диче-	кон-
	которые изучаются на лекции	ческого	ские	троля
		занятия	посо-	знаний
			бия

1.	Понятие об уравнении линии на плоско-		4, 5, 8,
сти. Прямая на плоскости как линия 1-го по-			4, 5, 8,
сти. Прямая на плоскости как линия 1-го по-			9, 12,
рядка. Уравнение прямой на плоскости по			9, 12,
рядка. Уравнение прямой на плоскости по		I	13, 18,	ПДЗ
точке и нормальному вектору (направляю-		I	13, 18,	ПДЗ
точке и нормальному вектору (направляю-			21, 22,
щему вектору, угловому коэффициенту), по			21, 22,
щему вектору, угловому коэффициенту), по			25
двум точкам, в «отрезках».			25
двум точкам, в «отрезках».
2. Расстояние от точки до прямой. Взаим-			4, 5, 8,
ное расположение двух прямых на плоско-			9, 12,	Опрос
сти. Линии 2-го порядка на плоскости. Эл-		II, III	13, 18,	Опрос
липс, гипербола, парабола.			21, 22,
			25
3.	Понятие уравнения поверхности в про-		4, 5, 8,
странстве. Плоскость как поверхность 1-го			4, 5, 8,
странстве. Плоскость как поверхность 1-го			9, 12,
порядка. Уравнение плоскости по точке и			9, 12,
порядка. Уравнение плоскости по точке и		IV	13, 18,	Р, ПДЗ
нормальному вектору, в «отрезках», по трем		IV	13, 18,	Р, ПДЗ
нормальному вектору, в «отрезках», по трем			21, 22,
точкам. Угол между плоскостями. Расстоя-			21, 22,
точкам. Угол между плоскостями. Расстоя-			25
ние от точки до плоскости.			25
ние от точки до плоскости.
4. Прямая в пространстве, как линия пере-			4, 5, 8,
сечения двух плоскостей. Уравнения прямой			9, 12,
в пространстве по точке и направляющему		V, VI	13, 18,	Р, ПДЗ
вектору, по двум точкам. Взаимное распо-			21, 22,
ложение прямой и плоскости.			25
5. Поверхности 2-го порядка в пространст-			4, 5, 8,
ве. Эллипсоид, гиперболоиды, конус 2-го			9, 12,	ИДЗ,
порядка, параболоиды, цилиндры 2-го по-		VII	13, 18,	ИДЗ,
порядка, параболоиды, цилиндры 2-го по-		VII	13, 18,	опрос
рядка. Метод сечений.			21, 22,	опрос
			25
	Принятые сокращения:
	ПДЗ – проверка домашнего задания;
	Р − разминка
	ИДЗ – индивидуальное домашнее задание;
	101

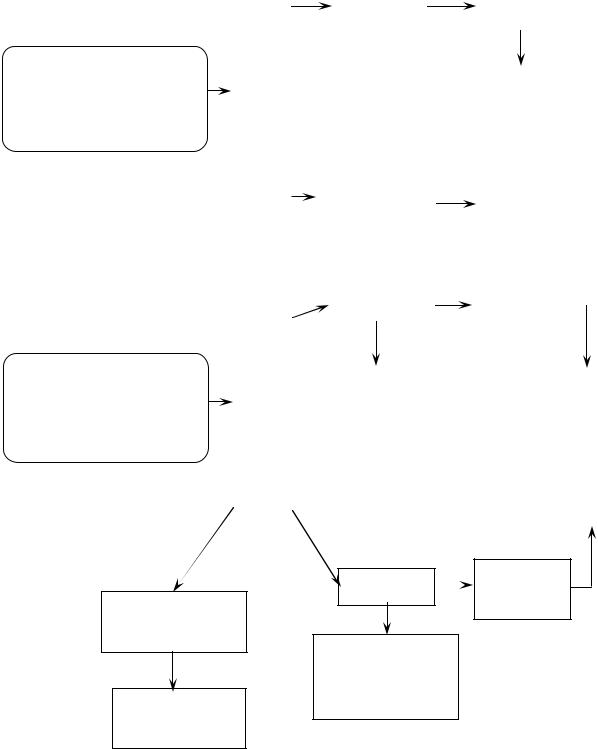
ГРАФИЧЕСКАЯ СХЕМА МОДУЛЯ

Способы

Прямая

задания

АНАЛИТИЧЕСКАЯ

Взаимное рас-

ГЕОМЕТРИЯ

положение

на

плоскости

М Н

А А

Кривые 2-го

Канонические

порядка

уравнения

					Способы
				Плоскость	Способы
				Плоскость	задания

	С	К
		К
		О
АНАЛИТИЧЕСКАЯ	И	О
АНАЛИТИЧЕСКАЯ	И	О		Взаимное	Взаимное рас-
ГЕОМЕТРИЯ	С	Р		Взаимное	Взаимное рас-
ГЕОМЕТРИЯ	С	Р	расположение		положение
в	Т	Д	расположение		положение
в	Т	Д		плоскостей	прямой и плос-
пространстве	Е	И		плоскостей	прямой и плос-
пространстве	М Н				кости, угол
	М Н				кости, угол
	А А				между прямой
		Т			и плоскостью

Прямая

Способы

Поверхности 2-го порядка

задания

Взаимное рас- положение

прямых

Канонические

уравнения

102

ИНФОРМАЦИОННАЯ ТАБЛИЦА

«АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ»

Аналитическая геометрия на плоскости

1. Общее уравнение прямой

Всякое уравнение первой сте- пени относительно двух пере- менных определяет прямую на плоскости Аx+ВУ+C=0.

2. Уравнение прямой, прохо- дящей через данную точку в данном направлении

у-у0=k(х-х0).

3. Уравнение прямой линии на плоскости, проходящей через

данную точку М0(х0, у0), перпендикулярно дан-

ному вектору N ( A, B) .

N× M 0M = 0 , А(х - х0 ) + В( у - у0 ) = 0 .

4.Уравнение прямой линии, проходящей через две точки

М1М 2 = (х2 - х1, у2 - у1) М1M = (х - х1, у - у1)

х- х1 = у - у1 .

х2 - х1 у2 - у1

5. Каноническое и параметрические уравнения прямой линии на плоскости

1. Каноническое

уравнение прямой

2. Параметрические уравнения прямой на

на плоскости, проходящей через точку

плоскости, проходящей через точку

М0(х0, у0)

с направляющим вектором

М0(х0, у0) с направляющим вектором

х - х

у - у

х = х

+ mt

s(m, n)

s(m, n) , M 0M = t × s ,

или

у = у0 + nt

6. Уравнение прямой линии в отрезках

7. Расстояние d от М0(х0, у0) до прямой

у - 0

х - а

, а×b ¹ 0

, или

= 1.

Ах+Ву+С=0,

d =

Aх0 + Ву0

+ С

b - 0 0 -

a b

А2 + В2

8. Угол между прямыми на плоскости

Пусть

прямые

заданы

общими

уравнениями

L1 : A1x + B1 y + C1 = 0 ,

L2 : A2 x + B2 y + C2 = 0 , тогда cos (L1, L2 ) = cos (

2 ) =

1 ×

1. Пусть L1 и L2 заданы каноническими уравне-

Пусть L1 и L2 заданы уравнения-

ниями

L :

x - x1

y - y1

x - x2

y - y2

ми

угловыми

коэффициентами

L1 : y = k1x + b1 , L2 : y = k 2 x + b2 ,

тогда cos (L1, L2 ) = cos (

2 ) =

1 ×

тогда tg (L1, L2 ) = tg j = tg (b - a) =

s 2

tg b - tg a

k2 - k1

1+ tg b× tg a

1+ k2 ×k1

9. Взаимное расположение двух прямых на плоскости

Пусть заданы две прямые своими общими уравнениями (все остальные способы мож-

но к этому свести): L1 : A1x + B1 y + C1 = 0 ,

L2 : A2 x + B2 y + C2 = 0 . Тогда прямые L1 и L2:

- совпадают,

- параллельны и не совпадают,

- пересекаются

L º L

L ║ L

L Ç L

= M

;

103

Аналитическая геометрия в пространстве

1. Плоскость в пространстве

Ах+Ву+Сz+D=0 – общее уравнение плоскости

1) А(х-х0)+В(у-у0)+С(z-z0)=0 – уравнение плос-

кости проходящей через точку М(х0;у0;z0)

n( А, В, С) .

2) Уравнение плоскости, проходящей через точ-

ку, || двум векторам

, M α Û

= 0

M 0M

х - х0

y - y0

z - z0

a x

a y

a z

= 0 .

b y

3) Уравнение плоскости проходящей через две

точки, || вектору

M(x, y, z) α Û

M 1M ×M1M 2 ×

= 0

x - x1

y - y1

z - z1

x2 - x1

y2 - y1

z2 - z1

= 0 .

ах

ау

аz

4) Уравнение плоскости проходящей через три точки M(x, y, z) α Û M1M × M1M 2 × M1M 3 = 0

x - x1	y - y1	z - z1
x - x1	y - y1	z - z1
x2 - x1	y2 - y1	z2 - z1	= 0
x3 - x1	y3 - y1	z3 - z1

2. Прямая в пространстве

	А х + В у + С z + D = 0				– общее
	1	1	1	1	– общее
	А2 х + В2 у + С2 z + D2 =				0
уравнение прямой
Параметрические уравнения пря-
мой
			х = х0 + mt,
				+ nt,
			у = у0	+ nt,
				+ pt,
			z = z0	+ pt,

где t коэффициент пропорцио- нальности

Канонические уравнения прямой

х- х0 = у - у0 = z - z0 = t m n p

Канонические уравнения прямой, проходящей через точки

M 1(х1, у1, z1) , M 2 (х2 , у2 , z 2 )

х- х1 = у - у1 = z - z1

х2 - х1 у2 - у1 z2 - z1

Расстояние от точки до плоскости

1. if M 1 удовлетворяет уравнению L, то

d(M1, L) = 0 .

2.if M 1 L , то

d (M 1, a) = Ax1 + By1 + Cz1 + D . A2 + B 2 + C 2

Угол между плоскостями

Пусть заданы две плоскости

a1 : A1x + B1 y + C1z + D1 = 0 ,

a2 : A2 x + B2 y + C2 z + D2 = 0 .

cos (a1, a 2 ) = cos (

2 )

1 ×

Взаимное расположение плоскостей

Пусть заданы общие уравнения двух плоскостей: a1 : A1x + B1 y + C1z + D1 = 0 , a2 : A2 x + B2 y + C2 z + D2 = 0 . Тогда возможны следующие случаи:

º a

;

Û A A + B B

+ C C

= 0 a

^ a

;

Û a

Ç a

= {L} .

a2 ;

104

Взаимное расположение двух прямых в пространстве

Пусть

L :

x − x0

y − y0

z − z0

L :

x - x0 ' =

y - y0

z - z0

1. L º L1 Û

3. L Ç L1 = {M1} Û

4. Пусть L и L1 скрещиваю-

1 M 0M 0 '

′

щиеся Û

1 M 0M 0 '¹ 0.

5. Расстояние между скре-

L º L1

M 0M 0 '= 0,

щивающимися

прямыми:

M 0

d ( L, L1 ) =

S S1 M 0 M 0 '

S ´ S1

2. L L1 Û S S1 , но

0¢

0 S

M 0

M ′

′

Расстояние от точки до прямой

Угол между двумя прямыми в

L :

x - x0

y - y0

z - z0

М1(х1, у1, z1)

пространстве

cos (L1, L2 ) = cos (

2 ) =

S 2

d (M 1, L) =

M 0M1

×sin a =

0M 1

×sin (M 0M

S ).

Взаимное расположение прямой и плоскости

Пусть прямая L задана каноническими уравнениями x - x0 = y - y0 = z - z0 , плоскость m n p

a - общим уравнением

1) L α

1.S ^ n Û S × n = 0 .

2.M 0 Îa Û

Ax0 + By0 + Cz0 + D = 0

a S

Ax + By + Cz + D = 0 . В пространстве прямая и плоскость могут:

2) L α

3) L Ç a = {M1}

= 0

2. M 0 Ïa Û

¹ 0

Ax0 + By0 + Cz0 + D ¹ 0

M 0

S a

Угол между прямой и плоскостью

Пусть заданы плоскость

α : Ax + By + Cz + D = 0 и прямая L : x - x0 = y - y0 = z - z0 .

m	n	p
sin b =		Am + Bn + Cp
		Am + Bn + Cp


	A2 + B 2 + C 2 × m 2 + n 2 + p 2
	A2 + B 2 + C 2 × m 2 + n 2 + p 2

Определение точки пересечения

прямой и плоскости

L Ç a = {M1} Û S × n ¹ 0 .

Ax + By + Cz + D = 0,

		+ mt,
x = x0		+ mt,
		.
y = y	0	+ nt,
		+ pt.
z = z0		+ pt.

105

Невырожденные кривые второго порядка на плоскости

1. Эллипс

x 2

y 2

2. Гипербола

x 2

y 2

a 2

b 2

a 2

b 2

Важные характеристики:

1. Координаты

фокусов:

F1 (-c; 0) , F2 (c; 0) , c 2 = a 2 - b 2 2. A1 (-a; 0) , A2 (a; 0) , B1 (0; -b) ,

B2 (0;b) - координаты вершин эл- липса

3.	e =	c	,			(e < 1)	- эксцентриси-

тет		a

4.	x = ±				a	- уравнения директрис.
					e

5.	e =	r		,		где r	- расстояние от

		d

точки эллипса до фокуса; d - рас- стояние от точки эллипса до од- носторонней директрисы.

r1	= ex - a	- фокальные ра-
6.		- фокальные ра-
r2	= ex + a

диусы точек эллипса.

Важные характеристики:

7.Координаты фокусов:

F1 (-c; 0) , F2 (c; 0) , c 2 = a 2 + b 2 .

8. A1 (-a; 0) , A2 (a; 0) - координаты вершин гиперболы.

9. e = c , (e > 1) . a

10.y = ± b × x - уравнения асимптот.

11. x = ± ae - уравнения директрис.

12. e = r , где r - расстояние от точки гипер- d

болы до фокуса; d - расстояние от точки ги- перболы до односторонней директрисы.

r1	= ex - a	- фокальные радиусы правой
13.		- фокальные радиусы правой
r2	= ex + a
ветви гиперболы;
r3	= -ex + a	- фокальные радиусы левой
r4 = -ex - a		- фокальные радиусы левой
r4 = -ex - a

ветви гиперболы.

3. Парабола

1. x 2 = 2 py

2. x 2 = −2 py

3. y 2 = 2 px

4. y 2 = −2 px

106

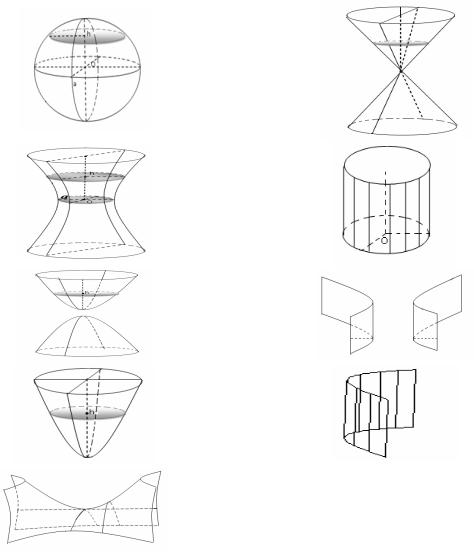
Поверхности 2-го порядка

Поверхностью второго порядка называют поверхность, заданную алгебраиче- ским уравнением второй степени.

Ах2+Ву2+Сz2+ Dху+Eхz+Gуz+Mх+Ну+Nz+F=0

где А2 + В2 + С2 ¹ 0 .

Поверхность второго порядка можно разбить на классы основных невырожден-

ных поверхностей, имеющих одну и ту же форму канонического уравнения:

1) эллипсоид,

4) конус второго поряд-

эллиптический

ци-

однополостный ги-

ка,

линдр,

перболоид,

эллиптический пара-

гиперболический ци-

двуполостный гипер-

болоид,

линдр,

болоид,

гиперболический па-

параболический

ци-

раболоид,

линдр

= 1

−

= 0

эллипсоид

конус

−

= 1

однополостный

эллиптический

гиперболоид

цилиндр

−

= −1

−

= 1

двуполостный

гиперболический

гиперболоид

цилиндр

x 2

y 2

= 2z

x2 = 2 py

p 2

q 2

параболический

эллиптический

цилиндр

параболоид

x 2

−

y 2

= 2z

p 2

q 2

гиперболический

параболоид

107

5.1. Алгебраические линии.

Прямая на плоскости – линия первого порядка. Способы задания прямой

Определение 5.1.1. Уравнением линии на плоскости Oxy назы-

вается такое уравнение F ( x, y ) = 0 с двумя переменными, которому удов-

летворяют координаты точек (x, y), лежащих на линии, и только они. Пе- ременные x и y называют координатами точек заданной линии.

Замечание 5.1.1. Уравнение линии позволяет изучение геомет- рических свойств линии заменить исследованием ее уравнения.

Замечание 5.1.2. В аналитической геометрии на плоскости мы будем рассматривать задачи двух типов:

1. По уравнению линии определить её вид, геометрические свойст- ва, расположение на плоскости.

2. Зная геометрические свойства линии, задать её аналитически – уравнением или системой уравнений, связывающих её координаты.

Замечание 5.1.3. В аналитической геометрии провести прямую означает описать её уравнением, связывающим координаты точек этой прямой.

Задача 1 (задание прямой точкой и углом наклона к оси Ох).

Провести

прямую

через точку

M 0 ( x0 , y0 )

под

углом

оси Ох

(рис. 1).

M 0 ( x0 , y0 ) L,

Дано:

угол ме-

жду ( L,Ox) = α .

Найти: уравнение L .

Решение.

Возьмём

произ-

вольную

точку

M (x, y) L

и рас-

смотрим

прямоугольный

М0АМ. В

треугольнике

М0АМ,

tg α =

y − y0

;

tg α = k ; значит,

x − x0

Рис. 1

y − y0

M L k =

y − y0

= k ( x − x0 ) .

(5.1.1.)

x − x0

y = kx + (−kx0 + y0 ) или

Уравнение (5.1.1.) можно переписать в виде

y = kx + b .

(5.1.2)

108

Вывод: Прямую на плоскости можно задать точкой и углом на- клона к положительному направлению оси Ox , или его тангенсом (угло- вым коэффициентом).

Определение 5.1.2. Уравнение вида (5.1.2) называют уравнением прямой с угловым коэффициентом k.

Определение 5.1.3. Если уравнение линии (L) в ДПСК имеет вид P ( x, y ) = 0 , где P − многочлен n-ной степени, то говорят, что задана алгеб-

раическая линия n-го порядка.

Например, прямая y = kx + b − линия первого порядка, а парабола

y = ax 2 + bx + c , окружность x 2 + y 2 = R 2 − алгебраические линии второго

порядка.

Графики же логарифмических функций, тригонометрических функ- ций и т.п. не являются алгебраическими линиями, их называют трансцен-

дентными линиями.

ТЕОРЕМА 5.1.1. Уравнение Ax + By + C = 0 (*) задает прямую на плоскости.

Доказательство. В уравнении (*) возможны два случая:

1. B = 0 , тогда Ax + C = 0 . Если А=0, то уравнение (*) теряет смысл,

поэтому очевидно A ¹ 0 , следовательно

x = −

− прямая, параллельная

оси Оy, т.е. имеет вид x=a.

2. B ¹ 0 ,

тогда

(*) преобразуется

к эквивалентному уравнению

By = -C - Ax ,

y = −

x −

. Обозначим −

= k ,

−

= b , таким образом,

имеем, что уравнение (*) принимает вид y = kx + b , которое задает уравне-

ние прямой на плоскости.
Замечание 5.1.4.	По определению 5.1.3 уравнение (*) является
линией 1-го порядка на плоскости.
Определение 5.1.4.	Уравнение Ax + By + C = 0	называется об-

щим уравнением прямой на плоскости.

5.2. Способы задания прямой на плоскости

Определение 5.2.1. Вектор, перпендикулярный данной прямой, называется вектором нормали данной прямой (нормальным вектором).

Обозначается: n, N , n L .

109

Задача 1

(задание прямой точкой и вектором нормали).

Провести прямую L,

проходящую через точку M 0 ( x0 , y0 ) , перпен-

дикулярно вектору

( A, B) (рис. 2).

Дано:

M 0 L ,

перпендикулярен L.

М0(х0, у0) М(х, у)

Решение.

Возьмём произвольную

точку

( x, y )Î L ,

тогда M 0 L Û

Рис. 2

M 0M

= 0

векторное уравнение искомой

M 0M

прямой.

= ( x - x0 , y - y0 )

= A( x - x0 ) + B ( y - y0 ) ,

значит

M 0M

A( x - x0 ) + B ( y - y0 ) = 0 . Таким образом, получили

A( x - x0 ) + B ( y - y0 ) = 0

(5.2.1)

уравнение, которому должны удовлетворять координаты произвольной точки прямой.

Докажем, что это уравнение действительно описывает прямую. Из

(5.2.1) следует Ax + By + (-Ax0 - By0 ) = 0 .	Обозначим (-Ax0 - By0 ) = C .
Значит, (5.2.1) равносильно Ax + By + C = 0	(*) - общему уравнению пря-

мой. По теореме 5.1.1 оно задает прямую на плоскости.

Вывод: прямую на плоскости можно задать точкой и нормальным вектором.

Определение 5.2.2. Вектор, имеющий направление заданной пря- мой, называется направляющим вектором данной прямой. Обозначается:

s, q, a, S L .

Задача 2 (задание прямой точкой и направляющим вектором).

Провести прямую L на плоскости,

проходящую

через точку

M 0 ( x0 , y0 ) в направлении вектора

(m, n) (рис. 3).

Дано: M 0

L , S ║L.

S (m, n)

Найти: уравнение L.

M (x, y)

Решение.

Пусть M ( x, y )Î L , тогда выпол-

няется условие M ( x, y )Î L Û

║

(по ус-

M 0 (x0 , y0

M 0M

Рис. 3

ловию коллинеарности).

- x0

y - y0

(5.2.2)

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 2211 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб45умк_Цывис_Функции_Интеграл. исчисл..pdf