Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Диф.уравнения_Ряды

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

5.68 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 227 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

2.7. Особые решения

Рассмотрим задачу Коши
	y′ = f (x, y) ,		(1)
	y(x0 ) = y0 .		(2)
Справедлива теорема о существовании и единственности решения
задачи Коши.
Теорема 1.	Если функция f(x,y) и ее частная производная	f	′(x, y)
			y
непрерывны в некоторой замкнутой области D плоскости Oxy,		содержа-
щей точку (x0,y0),	то существует единственное решение y = y(x)	уравне-

ния (1), определенное в интервале (x0 – ε, x0 + ε) и удовлетворяющее усло-

вию (2).

Другими словами: при любых начальных условиях в области D су- ществует единственное решение, если только f(x,y) удовлетворяет поло- женным условиям.

С геометрической точки зрения это означает, что через каждую внутреннюю точку (x0,y0) области D проходит единственная интеграль- ная кривая дифференциального уравнения (1).

Точки плоскости xOy, через которые проходит более чем одна инте- гральная кривая дифференциального уравнения, называются особыми точ- ками этого уравнения.

Интегральная кривая дифференциального уравнения первого поряд- ка называется особой, а соответствующее ей решение – особым решением дифференциального уравнения, если через каждую ее точку проходит, по крайней мере, еще одна интегральная кривая этого уравнения.

Пример 1. Решить уравнение 1 − y2 dx − ydy = 0 .

Решение. Разделив переменные и интегрируя, получим

x = −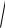1 − y2 + c или (x − c)2 + y2 = 1.

В общем интеграле (x − c)2 + y2 = 1 исходного дифференциального уравнения содержатся не все решения, т.к. при делении на 1 − y2 потеря-

ны решения y = ±1, которые нельзя найти из общего интеграла. Интеграль-

ные кривые исходного уравнения – семейство окружностей радиусом 1 с

центром в точках (c;0) и прямые y = ±1. Но через каждую точку прямых y = ±1 проходит еще одна интегральная кривая (окружность) исходного дифференциального уравнения. Значит y = ±1 – особые решения данного

уравнения.

Решение, в каждой точке которого нарушается единственность ре- шения задачи Коши, называется особым. Если в дифференциальном урав-

нении (1) функция f(x,y) непрерывна по переменным x				и y и имеет част-
ную производную по	y (ограниченную или нет), то особыми решениями
				∂f
могут быть только те кривые		y = ϕ(x) , во всех точках которых ∂y			обра-
щается в бесконечность.
Если семейство кривых		φ(x, y,c) = 0 , являющихся интегральными
кривыми уравнения		′	имеет огибающую	y = ϕ(x) ,	то она
	F (x, y, y ) = 0

представляет собой особую интегральную кривую этого же уравнения. Ес- ли функция φ(x, y,c) непрерывно дифференцируема, то огибающая вхо-

дит в состав кривой, определяемой системой уравнений

f(x, y,c) = 0,

¶f(x, y,c) =

¶ 0.

Пример 2. Найти особые решения уравнения y¢ = 3 y2 +1.
		+1 всюду непрерывна, но ∂f	=	2	×	1
Решение. Функция f (x, y) = 3	y2

		¶y	3			3 y
не ограничена в окрестности точки	(x0,0), следовательно, возможно суще-
ствование особого решения y = 0.	Но y = 0 – не решение исходного урав-

нения, значит, данное дифференциальное уравнение особых решений не имеет.

Пример 3.	Найти особые решения уравнения y¢ = 3 ( y - 2x)2 + 2 .
Решение.	Правая часть уравнения всюду непрерывна, но частная

производная по y
∂f =	2
¶y	33
¶y	33	y - 2x

обращается в бесконечность в точках на прямой y = 2x. Непосредственной проверкой устанавливает, что эта прямая – интегральная. Установим, что решение y = 2x – особое решение исходного уравнения. Найдем общее

решение этого дифференциального уравнения. Полагая y − 2x = t , получим

dt = 3t2 , т.е. x + c = 33t или, возвращаясь к переменным x и y, получим dx

27( y − 2x) = (x + c)3 .

Кривые этого семейства касаются прямой y = 2x при x0 = – c, т.е. в каждой точке интегральной кривой y = 2x нарушается единственность.

Следовательно, решение y = 2x –				особое решение.
Пример 4. Пусть общее решение некоторого дифференциального
уравнения первого порядка	y =		x2		+ cx + c2 . Найдите особые решения то-

	2
го же уравнения.
Решение. Дискриминантную кривую найдем из системы уравнений
		x		2
y −					− cx + c2 = 0

	2
			−x − 2c = 0.

(второе уравнение получено дифференцированием по c первого уравне-

ния). Исключив параметр с, получим y =	x2	– это кривая является оги-

4

бающей, т.к. выполнены условия для огибающей. Действительно, если

	x2		∂φ		∂φ
φ(x, y,c) = y −		− cx − c2 , то	∂x	= −(x + c) ;	∂y	= 1.
	2

Эти частные производные ограничены и одновременно не обраща-

ются в нуль, значит y = x2 – особое решение. 4

Замечание 1. В процессе интегрирования дифференциального урав- нения приходится выполнять действия, которые могут нарушить равно- сильность уравнения (например, деление на выражения, содержащие пе- ременные). В этих случаях требуется каждый раз проверять, не произойдет ли при этом потеря решений, которые могут оказаться особыми.

						2x
Пример 5. Решить уравнение							ydx + (1 − x2 )dy = 0 .
Решение. Разделяя переменные, имеем
	2x	dx +	dy		= 0	(1 − x2 = 0;			= 0) .
								y
1 − x2

				y

Общий интеграл -ln

1 - x2

+ 2

= c .

Из уравнения 1 − x2 = 0 находим x = ±1.

Функции x = 1

x = – 1

( y ¹ 0)

– частные решения исходного уравнения. Уравнение

= 0 дает

особое решение

y = 0 (x ¹ ±1) .

Решить уравнение xdy + x

- y dx = 0 .

Пример 6.

-1

Решение.

Данное уравнение однородное. Полагая y = u ×t ,

получим

xdt +

dx = 0

t -1

– уравнение с разделяющимися переменными,

которое

имеет общее решение 2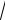t -1 + ln x = c и особое решение t =1, или, воз-

вращаясь к искомой функции y, получим		2	y	-1 + ln	x	= c –	общее реше-


ние, а y = x (x ¹ 0)	– особое решение.		x


Замечание 2.	Уравнение Бернулли	y¢ + p(x) y = g(x) yn					(n ¹ 0; n ¹1)
при 0 < n < 1, имеет особое решение y = 0.

Замечание 3. Если m = m(x, y) – интегрирующий множитель для дифференциального уравнения первого порядка, то кривые, в точках кото- рых m обращается в нуль или бесконечность, могут быть особыми реше- ниями данного дифференциального уравнения.

2.8. Уравнения, не разрешенные относительно производной

Уравнение первого порядка, неразрешенное относительно производ- ной, имеет следующий вид

′	(1)
F (x, y, y ) = 0 .

Если уравнение (1) разрешимо в элементарных функциях относи- тельно y′ , тогда получаем одно или несколько уравнений, разрешенных

относительно	y′ :
	y′ = fk (x, y)	(k = 1,2,3,...)	(2)
где fk (x, y)	– вещественные функции от x и y.
Интегрирование уравнения (1) сводится к интегрированию уравне-
ний (2).
Пример 1. Решить уравнение		( y¢)2 - 4 y = 0 .

Решение. Данное уравнение

два:

y′ = 2

распадается на

y′ = −2

y = (x + c)2 ;

(x ³ -c)

и второе –

тогда первое имеет решение

y = (x + c)2 ;

(x £ -c) .

Решением данного уравнения будет

y ≡ 0 .

Уравнение вида

′ ′

′

) = 0

(3)

F ((x, y, y ,( y )

,...,( y )

дифференциальное уравнение первого порядка n-ной степени. Если урав-

нение разрешимо (в элементарных функциях) относительно	y′ :
y′ = fk (x, y); (k = 1,2,..., m ≤ n) ,	(4)

то задача его интегрирования сводится к интегрированию уравнений (4).

Если каждое из уравнений (4) имеет общий интеграл
ϕk (x, y) = c;	(k = 1,2,..., m ≤ n) ,	(5)

тогда общим интегралом уравнения (3) является совокупность общих ин- тегралов (5). Общий интеграл (3) можно записать в виде одной формулы

(ϕ1(x, y) − c)(ϕ2 (x, y) − c)...(ϕm (x, y) − c) = 0 .

Если хоть одно из уравнений (4) имеет особые решения, то оно будет

особым решением и для уравнения (3).

Пример 2.

Решить уравнение

′

+ (4xy +

2x +1) y

′

- 2x = 0 .

2 y( y )

- (4xy + 2 y +1)( y )

Решение.

Решая кубическое уравнение относительно y′ ,

получим

y′ = 1; y′ = 2x ;

y′ =

. Интегрируя эти уравнения, получим

y = x + c ;

2 y

y = x2 + c ; y2 = x + c ,

тогда общий интеграл данного дифференциального

уравнения имеет вид

( y − x − c)( y − x2 − c)( y2 − x − c) = 0 . Особых решений

данное уравнение не имеет.

Пример 3.

Решить уравнение

′

− 2 y

′

+ 1 − y + x = 0 .

( y )

Решение.

Решая квадратное уравнение относительно y′ , получим

y′ = 1 + y − x; y′ = 1 − y − x .

Общее решение – y = x +	(x + c)	2	и особое решение – y = x	– огибающая
Общее решение – y = x +	4		и особое решение – y = x	– огибающая
	4
кривая общего решения.
Если дифференциальное уравнение содержит только y′ , т.е. имеет вид
			′	(6)
			F ( y ) = 0 ,	(6)
причем оно определяет хоть одно вещественное значение				y′ , то можно

найти все интегральные кривые этого уравнения без квадратур. Действи- тельно, если

y′ = ak	(k = 1,	2,	...)				(7)
вещественные корни уравнения (6), тогда		F (ak ) = 0;		(k = 1, 2,	3,	...) .
Из уравнения (7) находим	y = a x + c		(k = 1,	2, ...) или	a		=	y − c	,
						k
	k							x

поэтому уравнение (6) имеет множество интегральных кривых

F y − c = 0 .x

Найденное множество – общий интеграл (6). Отметим, интеграл (8) получается из дифференциального уравнения (6)

(8)

что общий заменой y′

на y − c . x

Пример 4. Решить дифференциальное уравнение ( y′)3 + ( y′)2 − y′ + 1 = 0 .

Решение. Общим интегралом данного уравнения будет

y − c 3		y − c 2		y − c
	+		−		+ 1 = 0 .

x		x		x

Если дифференциальное уравнение не содержит искомой функции, то есть оно имеет вид

′	(9)
F (x, y ) = 0	(9)
и разрешимо (в элементарных функциях) относительно y′ :
y′ = fk (x) (k = 1, 2, ...) ,	(10)
тогда y = ∫ fk (x)dx + c .

Отметим, что уравнения (10), а, следовательно, и (9) могут иметь

решения вида

x = a ,

(11)

которые могут быть особыми.

Пример 5.

Решить уравнение

( y¢)2 -

= 0 .

y′ , получим

Решение.

Решая квадратное уравнение относительно

y¢ = ±

, интегрируя, имеем y =

+ c ; y = −

+ c . Особое решение

будет

y ≡ 0 .

Если уравнение (9) трудно разрешимо относительно

y′ , то целесо-

образно ввести параметр t				и заменить уравнение (9) двумя уравнениями:
x = ϕ(t) и	y	′	= y(t) . Так как	′	′
				dy = y dx , то в данном случае	dy = y(t) × j (t)dt ,

откуда

y = ∫y(t) × j¢(t)dt + C ,

а, следовательно, интегральные кривые уравнения (9) определяются в па- раметрической форме следующими уравнениями:

x = ϕ(t) ,

y = ∫y(t)j¢(t)dt + C .

Если уравнение (9) разрешимо относительно		′	то почти
Если уравнение (9) разрешимо относительно		x, x = j( y ) ,	то почти
всегда удобно в	качестве параметра выбрать y′ = t . Тогда		x = ϕ(t) ,
dy = y¢dx = t × j¢(t)dt,	y = ∫tj¢(t)dt + C .

Пример 6. Решить уравнение ( y¢)3 − y¢ −1 − x = 0 .

x =

y =

Решение. Данное уравнение легко разрешимо относительно x, ( y′)3 − y′ −1. Полагая y′ = t , получим x = t3 − t −1, dy = y¢dx = t(3t 2 -1)dt ,

3t 4 - t2 + C .

4 2

Тогда семейство искомых интегральных кривых данного дифферен- циального уравнения в параметрической форме определяется формулами

x = t3		- t -1,

	3t	4		t	2
y =			-			+ C.
	4
			2

Пример 7. Решить уравнение			x	′	2		′	.
Пример 7. Решить уравнение			x	1 + ( y )		= y		.
Решение.	Пусть	y′ = tgt,			π	π		,	тогда	x = sin t ,
Решение.	Пусть	y′ = tgt,		t −		;		,	тогда	x = sin t ,
					2	2
′		y = − cost + C .
dy = y dx = tgt × costdt = sin tdt ,		y = − cost + C .
Исключая	t из уравнений		x = sin t ,					y = − cost + C		получим
x2 + ( y − c)2 = 1	семейство окружностей.
Если дифференциальное уравнение имеет вид
			′							(12)
		F ( y, y ) = 0 ,								(12)
и оно трудно разрешимо относительно				y′ , то, как и в предыдущем случае,

целесообразно ввести параметр t					и заменить уравнение (12) двумя урав-
нениями: x = ϕ(t) и y′ = y(t) .
Так как	′
	dy = y dx , то
		dy		′			′
	dx =		=	ϕ (t)dt	или	x = ∫	ϕ (t) dt + C .
				ψ(t)
		y′					ψ(t)

Значит, искомые интегральные кривые дифференциального уравне- ния (12) определяются уравнениями

∫ϕ′(t) dt + C и y = ϕ(t) .

ψ(t)

Вчастности, если уравнение (12) легко разрешимо относительно y,

′

. Действительно,

если

′

то за параметр удобно взять y

y = j( y ) , то, полагая

′

y′ = t , получим

y = ϕ(t), dx =

= ϕ

(t)dt , а

x = ∫ ϕ

(t)dt + C .

y′

′

+ y

′

− y + 5 = 0 .

Пример 8. Решить уравнение ( y )

+ ( y )

Решение.

Данное

уравнение

легко

разрешимо

относительно y:

′ 5

′

+ y

′

+ 5 .

y = ( y )

+ ( y )

Полагая y′ = t , получим

y = t5 + t3 + t + 5 ,

5t 4

+ 3t 2 + 1

5t4

3t 2

dx =

= 5t3

+ 3t

dt , x

+ ln

+ C .

y′

Уравнения

y = t5 + t3 + t + 5

и x =

5t4

3t 2

+ ln

+ C являются па-

раметрическими уравнениями семейства интегральных кривых.

Пример 9. Решить уравнение				y =	1 + ( y¢)2 .
Решение. Пусть y′ = sht , тогда					y = cht
dx =	dy	=	sht	dt = dt,		x = t + C .
			sht
	y¢
Исключая (это возможно)			из	y = cht		и x = t + C параметр t, полу-

чим y = ch(x − C) .

Рассмотрим общий случай уравнения (1)

F (x, y, y′) = 0 .

Заменим уравнение (1) его параметрическим представлением

x = ϕ(u,σ)

y = ψ(u,σ)

y′ = q(u,s)

(13)

Так как

′

dy = y dx , тогда имеем

¶y

¶j

du +

¶j

du +

¶s

ds = q(u,s)

¶u

¶s

¶u

откуда, выражая производную

dσ

, получим

¶j

¶y

q(u,s) ¶u

¶u

(14)

¶y

¶j

¶s - q(u,s)

¶s

уравнение первого порядка, уже разрешенное относительно производной, а значит можно искать решение, опираясь на методы, рассмотренные в пре- дыдущих параграфах. Отметим, что уравнение (14) далеко не всегда будет интегрироваться в квадратурах.

Если уравнение (1) легко разрешимо относительно y, то за парамет-

ры u и s удобно брать

x и

y′ . Действительно, если уравнение (1) при-

′

= p –

параметры, тогда получим

водится к виду y = f (x, y ) , то x

y = f (x, p), dy = ∂f

dx + ∂f

или

∂f

+ ∂f

, откуда

¶x

¶p

p =

∂f

(15)

¶x

¶p

¶x

Интегрируя уравнение (15) (если это удается) получим Φ(x, p,c) = 0 .

Совокупность уравнений Φ(x, p,c) = 0 и y = f (x, p) , где p – параметр,

определяющий семейство интегральных кривых исходного дифференци- ального уравнения.

Отметим, что уравнение (15) может быть получено дифференциро- ванием уравнения y = f (x, y′) по x.

Действительно, дифференцируя уравнение y = f (x, y′) по x и по-

лагая y′ = p , получим

p = ∂f + ∂f × dp , ¶x ¶p dx

а это уравнение (15). Поэтому этот метод называют интегрирование диф-

ференциальных уравнений с помощью дифференцирования.
Если уравнение (1) легко разрешимо относительно x, т.е.
						′		(16)
		x = f ( y, y ) ,						(16)
то выбрав за параметры	y и	y	′	= p и используя зависимость				′
то выбрав за параметры	y и	y		= p и используя зависимость				dy = y dx ,
получим
	dy = p				¶f dy +	¶f
	dy = p				¶f dy +	¶f	dp
					¶y	¶p

или			∂f	+ ∂f
	1	=			×	dp	.	(17)
			¶y
	p			¶p		dy
Интегрируя уравнение (17), получим
	Φ( y, p,c) = 0 .
Это уравнение и x = f ( y, p)				определяют интегральные кривые ис-

ходного уравнения. Отметим, что уравнение (17) может быть получено из уравнения (16) дифференцированием по y.

Рассмотренным методом в п. 2.6 решены уравнения Лагранжа и Клеро.

2.9. Приближенные методы решения дифференциальных уравнений первого порядка

Выше были рассмотрены некоторые классы дифференциальных уравнений первого порядка и методы их решения. Если ни один из них не приводит к решению задачи или требует сложных преобразований и вычис-

<<< < Предыдущая 1 2 3 4 5 67 / 227 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб40умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб35умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб45умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб93умк_Яско_ Диф.уравнения_Ряды.pdf