
14-es_1 / Высшая математика (РТФ) / умк_Цывис_Диф.уравнения_Ряды
.pdf
стояния от дна сосуда. Считаем, что высота уровня жидкости в емкости в момент времени t = 0 равна h, площадь сечения на высоте х равна S(x), а
площадь отверстия на дне емкости равна S. |
|
|
|
|
|
|
|
|
Известно, что скорость истечения жидкости v |
в тот момент, когда вы- |
|||||||
сота ее уровня равна х, определяется по формуле v = C × |
|
, где g = 9,8 |
м |
, |
||||
2gx |
||||||||
|
||||||||
|
|
|
|
|
с |
2 |
|
|
|
|
C = 0,6 ). |
|
|
|
|||
С – коэффициент, зависящий от типа жидкости (для воды |
|
|
|
|
||||
Считаем, что на бесконечно малом промежутке времени dt |
истече- |
|||||||
ние жидкости равномерно, а поэтому за промежуток времени dt |
вытекает |
|||||||
столбик (цилиндр) жидкости, высота которого vdt |
и площадь сечения S, |
|||||||
что приводит к понижению уровня жидкости в емкости на dx (т.е. имеем столбик (цилиндр) жидкости объема S (x)dx ). Приравнивая полученные
объемы, приходим к дифференциальному уравнению первого порядка с
разделяющимися переменными C × S × |
|
|
|
|
||
2gxdt = -S (x)dx . |
||||||
Учитывая начальное условие t(0) = h , |
|
приходим к математической |
||||
модели рассматриваемого процесса (задача Коши), который имеет вид |
||||||
dt = - |
S (x) |
|
, |
|||
|
|
|
|
|
||
|
|
|
|
|||
|
C × S × 2gx . |
|||||
t(0) = h.
Задачи для самостоятельной работы
1. yxdx + (x + 1)dy = 0 . Ответ: y = c(x +1)e− x , x = -1 . 2. y′ = cos( y − x) .
Ответ: y = x + 2pn, n Î Z; x + c = ctg y − x . 2
3. 2x2 yy¢ + y2 = 2 .
1
Ответ: y2 = ce x + 2 . 4. y¢ - xy2 = 2xy .
Ответ: y(ce− x2 -1) = 2; y = 0 . 5. (1 - x2 ) y¢ - xy = xy2 .
Ответ: y(c
 1 − x2 −1) = 1.
1 − x2 −1) = 1.
31

6. |
y¢ = (x − y)2 + 1. |
||
Ответ: y = x × |
1 |
. |
|
|
|||
|
|
x + c |
|
7. |
y′ = sin(x − y) . |
||
Ответ: x + c = ctg( y − x - π); y = x + pn, n Î Z . 2 4
8. y′ = ax + by + c .
Ответ: (ax + by + c)b = cebx . 9. (x + y)2 y¢ =1.
Ответ: x + y = tg( y + c) .
10. (Задача Лейбница 1684 г.) Найти все кривые, у которых длина подкасательной – постоянная, равная a.
x
Ответ: y = ce a .
11. Найти все кривые, у которых отрезок касательной, заключенный между осями координат, делится точкой касания в отношении m:n.
Ответ: c = xm yn . Если m = n , то xy = c .
12. В баке находится 100 л раствора, содержащего 10 кг соли. В бак непрерывно подается вода (5 л в мин), которая перемешивается с имею- щимся раствором. Смесь вытекает из бака с той же скоростью, что и пода-
ется вода. Сколько соли в баке останется через 1 ч.
−t
Ответ: количество соли x(t) =10e20 ; x(60) = 0,5 кг.
13. Найти все кривые, для которых площадь треугольника, образо- ванного касательной, ординатой точки касания и осью абсцисс, есть вели- чина постоянная, равная a2.
Ответ: 2a2 = y(c ± x) .
2.3. Однородные дифференциальные уравнения первого порядка
Определение. Функция f(x,y) называется однородной функцией по- рядка k относительно x и y, если справедливо тождество
f (tx,ty) = tk f (x, y), "t Î R .
32

Пример 1. f (x, y) = x2 + y2 |
– |
однородная функция порядка 2, |
т. к. |
||||||||||
f (tx,ty) = t2 f (x, y) . |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
однородная функция порядка |
2 |
, |
|
|
Функция |
f (x, y) = 3 x2 + y2 |
– |
т. к. |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
f (tx,ty) = t |
3 |
f (x, y) . |
|
|
|
|
|
||||||
Функция |
f (x, y) = |
2xy |
|
– |
однородная функция нулевого поряд- |
||||||||
x2 + y2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||
ка, т.к. f (tx,ty) = t0 × f (x, y) . |
|
|
|
|
|
||||||||
Дифференциальное уравнение первого порядка |
|
||||||||||||
|
|
|
|
|
|
|
y′ = f (x, y) |
(1) |
|||||
называется однородным, если f(x,y) – однородная функция нулевого порядка. Найдем общее решение дифференциального уравнения (1). Так как
уравнение (1) однородное, |
то |
f (x, y) = f (tx,ty) , полагая |
t = |
1 |
, получим |
||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
f (x, y) = f (1; |
y |
) . Полагая |
y |
|
= и или y = иx и y¢ = и + xи¢ |
и подставляя в |
|||||||||||||||
|
|
||||||||||||||||||||
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дифференциальное уравнение |
y¢ = f (1; |
y |
) , получим x ×и′ + u = f (1;u) или |
||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||
x |
du |
= f (1;u) - u . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Последнее уравнение – |
дифференциальное уравнение первого порядка |
|||||||||||||||||||
с разделяющимися переменными. Разделяя переменные, получим |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
du |
= |
dx |
, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
f (1;u) - u |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||
интегрируя которое, имеем |
∫ |
|
|
du |
= ln |
|
cx |
|
, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
f (1;u) - u |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и, подставляя вместо u отношение y , находим общее решение уравнения (1). x
Пример 2. Найти общее решение дифференциального уравнения
|
|
|
− |
x |
|
|
|
y¢ = |
xy + y |
2 × e |
y |
||||
|
|||||||
|
|
|
. |
||||
x |
2 |
|
|||||
|
|
|
|
|
|||
Решение. Так как правая часть данного уравнения – однородная функция, то исходное дифференциальное уравнение первого порядка – од-
33
нородное, |
поэтому, полагая |
|
y |
= u , y = u × x; y′ = xu′ + u и подставляя в дан- |
|||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||
ное уравнение, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
du |
+ u = u + u2e− |
|
|
или |
eu |
du = |
dx |
, |
||||||||||||
|
|
|
|
|
|
x |
u |
||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
u2 |
x |
||||||||
1 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда −e |
|
= ln |
|
x |
|
− c или e y |
+ ln |
|
x |
|
= C – |
|
|
|
|
|
|
|
|||||||||
u |
общийинтегралисходного уравнения. |
||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
Дифференциальное уравнение первого порядка |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
P(x, y)dx + Q(x, y)dy = 0 |
(2) |
|||||||||||||||||
называется однородным, если P(x,y) и Q(x,y) – однородные функции сво- их аргументов одного и того же порядка, непрерывные вместе со своими частными производными первого порядка.
Подстановка y = ux; dy = udx + xdu приводит однородное диффе- ренциальное уравнение первого порядка к дифференциальному уравнению с разделяющимися переменными.
Замечание 1. Решая уравнение (2) относительной производной, получим
|
|
dy |
= − |
P(x, y) |
= ϕ(x, y) |
(3) |
|
|
dx |
|
|||
|
|
|
Q(x, y) |
|
||
однородное дифференциальное уравнение типа (1), т. к. функции |
P(x,y) |
|||||
и Q(x,y) – |
однородные функции одного и того же порядка, а, следователь- |
|||||
но, ϕ(x,y) |
– однородная функция нулевого порядка. |
|
||||
Пример 3. Найти общее решение уравнения
(xy + y2 )dx − (2x2 + xy)dy = 0 .
Решение. Функции P(x, y) = xy + y2 и Q(x, y) = (2x2 + xy) – однород-
ные функции второй степени, следовательно, данное дифференциальное
уравнение – однородное. |
|
|
|
|
|
|
||||||
Полагая y = ux, |
dy = udx + xdu, |
после преобразования получим |
||||||||||
|
|
|
|
2 + u |
du = − |
dx |
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
u |
|
x |
|
|
|
|||
Интегрируя, получим 2ln u + u + ln x = c или |
u2 x = ce−u ( c = ec1 ). |
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|||
|
y |
|
|
|
|
|
|
|
− |
y |
|
|
|
|
|
|
|
|
|
|
|
||||
Так как u = |
, |
то общий интеграл имеет вид |
y2 = cxe x . |
|||||||||
|
||||||||||||
x
34

Замечание 2. К однородным уравнениям приводятся уравнения вида
|
|
|
|
|
|
|
|
|
|
ax + by + c |
|
|
|
|
|
|
|
|
|
|
|
y¢ = F |
|
|
, |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
a1x + b1 y + c1 |
|
|
|||
где |
|
C |
|
+ |
|
C1 |
|
¹ 0 . |
x = x1 + h, y = y1 + k, |
|
|||
|
|
|
|
|
|||||||||
С помощью преобразования |
где |
||||||||||||
|
|
|
|
|
|
|
|
|
|
ah + bk + c = 0 |
, |
|
|
ются решением системы уравнений |
a1h + b1k + c1 = 0 |
если |
|||||||||||
(4)
h и k явля-
a |
b |
¹ 0 , |
a1 |
b1 |
|
уравнение (4) приводится к однородному. |
|
|
|||||||
|
Уравнение (4) сводится к уравнению с разделяющимися переменны- |
||||||||
ми с помощью преобразования ax + by = t (или |
ax + by + c = t) |
в случае, |
|||||||
когда |
|
a |
b |
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
||||
|
|
a1 |
b1 |
|
|
|
|
|
|
|
Пример 4. |
Найти общее решение уравнения |
|
||||||
|
|
|
|
|
|
(2x − 4 y + 6)dx + (x + y − 3)dy = 0 . |
|
||
|
Решение. |
Данное уравнение приводится к однородному. Решая |
|||||||
|
|
|
|
|
|
2x - 4 y + 6 = 0 |
получим x0 = 1, y0 = 2. |
|
|
систему уравнений x + y - 3 = 0 |
Применяя |
||||||||
замену переменных x = x1 + 1 и y = y1 + 2, получим однородное уравне- |
|||||||||
ние |
|
(2x1 - 4 y1)dx1 + (x1 + y1)dy1 = 0 . |
Полагая |
y1 = u × x1 , |
получим |
||||
2x (1 - 2u)dx + x (1 + u)(udx + x du) = 0 или (2 - 3u + u2 )dx + x (1 + u)du = 0 . |
||||||||||||||||||||||||||||||||
1 |
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|||||
Выражение |
u2 + 3u - 2 |
|
|
равно нулю при |
u = 1 |
и |
u = 2, поэтому |
|||||||||||||||||||||||||
функции |
u = 1 |
и |
u = 2 являются решениями этого уравнения. Остальные |
|||||||||||||||||||||||||||||
решения получим, разделяя переменные |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
(1 + u)du |
+ |
dx1 |
= 0 |
или |
|
|
3 |
|
|
- |
|
2 |
|
du + |
dx1 |
= 0 . |
|
|||||||||||||
|
|
u2 - 3u + 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
x1 |
|
|
|
|
|
|
u - 2 |
|
|
u -1 |
|
|
x1 |
|
|
||||||||||||||
Интегрируя, получим ln |
|
x |
|
|
+ ln |
|
u - 2 |
|
3 |
= ln C |
или |
x |
(u - 2)3 |
= C , |
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
(u -1) |
2 |
|
|
|
|
|
|
|
1 |
|
(u -1)2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x (u - 2)3 |
= C(u -1)2 |
|
|
|
|
|
|
|
y |
|
3 |
|
|
|
y |
2 |
|
|
|||||||||||||
то есть |
или x |
|
1 |
- |
2 |
= C |
1 |
-1 |
откуда имеем |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
x1 |
|
|
|
|
|
x1 |
|
|
|
|||||||||
( y - 2x )3 |
= C( y - x )2 |
, возвращаясь к x и y получим |
|
||
1 |
1 |
1 |
1 |
|
|
|
|
|
|
( y - 2x)3 = C( y - x -1)2 . |
(5) |
35
Равенствам u = 1 и u = 2 в переменных x |
и y соответствуют ре- |
|||||
шения исходного уравнения y = x + 1 и y = 2x. Решение y = 2x |
получаем |
|||||
из общего решения (2) при С = 0. |
|
y + 2 |
|
y − 2x |
|
|
Пример 5. Найти общее решение уравнения |
y′ = |
+ tg |
. |
|||
|
|
|||||
|
|
x + 1 |
x + 1 |
|||
Решение. Данное уравнение становится однородным, если положить x + 1 = x1 и y + 2 = y1, поэтому заменой переменных y1 = x1u , x = x1 – 1 и y = ux1 – 2 приводим исходное уравнение к уравнению с разделяющимися
|
du |
|
ux1 − 2 − 2(x1 −1) |
|
|
|
|
du |
||||||||||||||||
переменными x1 |
|
+ u = u + tg |
|
|
|
|
|
или |
x1 |
|
= tg(u − 2) . Раз- |
|||||||||||||
dx |
|
x |
dx |
|||||||||||||||||||||
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
деляя переменные, получим |
|
du |
= |
dx1 |
или |
ln |
|
sin(u − 2) |
|
= ln |
|
x |
|
+ ln |
|
C |
|
|
||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
tg(u − 2) |
|
x1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
или sin(u − 2) = Cx1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отметим, что функция |
u - 2 = kp(k Î Z ) – |
решение данного уравне- |
||||||||||||||||||||||
ния, которое получаем из общего решения при С = 0. |
Возвращаясь к пере- |
|||||||||||||||||||||||
менным x и y, получим |
|
|
|
|
|
||
|
y + 2 |
− 2 |
|
= c(x + 1) |
или c(x + 1) = sin |
y − 2x |
|
sin |
|
|
|
. |
|||
x + 1 |
|
||||||
|
|
|
|
|
x + 1 |
||
2.4. Линейные дифференциальные уравнения
Линейным дифференциальным уравнением первого порядка относи-
тельно переменной y называется уравнение: |
|
y′ + P(x) y = Q(x) , |
(1) |
где P(x) и Q(x) – функции переменной x или постоянные числа.
Если в уравнении (1) Q(x) = 0, то уравнение называется линейным однородным, в противном случае – линейным неоднородным.
Рассмотрим методы интегрирования уравнения (1).
Метод И. Бернулли
Суть метода И. Бернулли состоит в следующем: |
общее решение |
уравнения (1) будем искать в виде произведения двух функций |
|
y = u(x) × s(x) . |
(2) |
Одна из этих функций произвольная (но не равная нулю), а другая должна быть определена так, чтобы произведение удовлетворяло линей- ному уравнению (1).
36

|
|
Действительно, |
любую функцию |
|
y(x) |
|
можно представить в виде |
|||||||||||||||||||||||||||
|
y(x) = |
y(x) × s(x) |
= u(x) × s(x); |
s(x) ¹ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
s(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференцируя равенство (2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
′ |
|
|
′ |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
(3) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= u σ + σ u |
|
|
|
|
|
|
|
|
|
||||||||||||
и подставляя (2) и (3) в (1), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
′ |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
||||||
|
|
|
|
|
|
|
|
|
|
u |
σ + u(σ + P(x)σ) = Q(x) . |
|
|
|
|
|
||||||||||||||||||
|
|
Подбираем хотя бы одну функцию s(x) |
такую, чтобы |
σ′ + P(x)σ = 0 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
Полученные уравне- |
|||||||
в (4), а, тогда из уравнения (4) получим u σ = Q(x) . |
||||||||||||||||||||||||||||||||||
ния – |
уравнения с |
разделяющимися |
|
переменными. |
|
Действительно, |
||||||||||||||||||||||||||||
|
dσ |
= -P(x)dx , |
|
|
т.е. |
|
s(x) = ce |
−∫ P( x)dx |
, |
|
|
полагая |
c |
|
= |
1, |
получим |
|||||||||||||||||
|
s |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s(x) = e |
−∫ P( x)dx |
, тогда s |
du |
= Q(x) |
|
или |
|
du |
|
= Q(x)e |
∫ P( x)dx |
, т.е. |
|
|
|
|||||||||||||||||||
|
dx |
|
|
dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
u(x) = ∫Q(x)e |
∫ P( x)dx |
dx + C . |
|
|
|
|
|
(5) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Тогда общее решение уравнения (1) |
имеет вид |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
y = u(x) × s(x) = (∫Q(x)e∫ P( x)dx dx + c)× e−∫ P( x)dx . |
|
|
|
|
|
||||||||||||||||||||||||
|
|
Пример 1. |
Найти частное решение уравнения |
xy¢ - 3y = x2 , |
|
удовле- |
||||||||||||||||||||||||||||
творяющее условию y(1) = 2. |
|
|
|
|
|
|
|
|
|
′ |
|
|
′ |
|
′ |
|
|
|
|
|
|
|
|
|||||||||||
|
|
Решение. |
Пусть |
y = u × s, |
|
тогда |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
= u σ + σ u . Подставляя эти со- |
|||||||||||||||||||||||||||||
отношения в исходное уравнение, получим |
|
xu¢s + xus¢ - 3us = x2 или |
||||||||||||||||||||||||||||||||
|
xu¢s + u(xs¢ - 3s) = x2 . Откуда |
xs′ - 3s = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
s = |
x2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xu¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Решая первое уравнение из совокупности, получим |
dσ |
= 3 |
dx |
, т.е. |
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
x |
||
s = x3 , |
тогда du = |
dx |
, т.е. u = C - |
1 |
. Следовательно, |
искомое общее ре- |
||||||||||||||||||||||||||||
x2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
шение исходного дифференциального уравнения –
y= u × s = x3 C - 1 = Cx3 - x2 .
x
Найдем частное решение, удовлетворяющее условию y(1) = 2 (зада- ча Коши)
2 = c · 1 – 1, т.е. c = 3.
37
Искомое частное решение имеет вид
y = 3x3 − x2 .
Метод Лагранжа (метод вариации произвольной постоянной)
Суть метода вариации произвольной постоянной интегрирования ли- нейного дифференциального уравнения первого порядка (1) состоит в сле-
дующем: общее решение дифференциального уравнения y′ + P(x) y = Q(x)
будем искать в виде общего решения соответствующего однородного уравнения
y′ + P(x) × y = 0 , |
(6) |
считая произвольную постоянную этого решения непрерывной функцией от x, т.е. C = C(x).
Находим общее решение соответствующего однородного уравнения
y′ + P(x) y = 0 |
– это уравнение с разделяющимися |
переменными, т.е. |
||
dy |
= -P(x)dx |
или |
|
|
|
|
|
||
y |
|
|
|
|
|
|
y = C × e |
−∫ P( x)dx |
(7) |
|
|
|
||
есть общее решение однородного дифференциального уравнения (6). Об-
щее |
решение |
линейного |
дифференциального |
уравнения |
(1) |
||||||
y′ + P(x) y = Q(x) |
будем искать в виде общего решения (7) однородного |
||||||||||
уравнения (6), считая постоянную |
|
С в формуле (7) непрерывной диффе- |
|||||||||
ренцируемой функцией от переменной x, |
т.е. |
|
|
|
|||||||
|
|
y = C(x) × e |
− |
∫ |
P( x)dx |
. |
|
(8) |
|||
|
|
|
|
|
|
||||||
|
Дифференцируя (8), получим |
|
|
|
|
|
|
|
|||
|
|
y¢ = C¢(x)e−∫ P( x)dx - C(x) × P(x)e−∫ P( x)dx . |
|
(9) |
|||||||
|
Подставляя (8) и (9) в уравнение (1), после приведения подобных |
||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
C¢(x) × e−∫ P( x)dx = Q(x) . |
|
|
(10) |
||||||
|
Откуда C¢(x) = Q(x) × e∫ P( x)dx |
и, |
интегрируя последнее уравнение, |
||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
C(x) = ∫Q(x) × e |
∫ |
P( x)dx |
dx + C . |
|
(11) |
||||
|
|
|
|
|
|
||||||
38
Тогда общее решение исходного уравнения имеет вид (в формулу (8) подставим (11))
y = e−∫ P( x)dx × |
∫Q(x)e∫ P( x)dx dx + C . |
|
|
Пример 2. |
Решить уравнение y¢ + y cos x = e− sin x . |
Решение. |
Найдем общее решение соответствующего однородного |
уравнения y′ + y cos x = 0. |
|
|
|
||
|
dy |
= -cos xdx; y = Ce− sin x |
– общее решение однородного уравнения. |
||
|
|
||||
|
y |
|
|
|
|
Решение исходного уравнения будем искать в виде y = C(x)e− sin x , то |
|||||
|
|
y¢ = C¢(x)e− sin x - C(x)cos xe− sin x . |
|||
Тогда, подставляя y и |
y |
′ |
′ |
||
|
в исходное уравнение, получим C (x) = 1 |
||||
или C(x) = x + C , и, следовательно, общее решение y = (x + C)e− sin x .
Метод Эйлера (интегрирования дифференциальных уравнений первого порядка)
Пусть дано линейное дифференциальное уравнение (1)
y′ + P(x) y = Q(x) .
Суть метода Эйлера при интегрировании уравнения (1) состоит в следующем: левая часть уравнения (1) есть производная произведения
двух функций – |
|
одна из которых |
y. Умножая (1) на e |
∫ P( x)dx |
, получим |
||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
y¢e∫ P( x)dx + yP(x)e∫ P( x)dx = Q(x)e∫ P( x)dx или |
(y × e∫ P( x)dx )¢ = Q(x)e∫ P( x)dx , |
|||||||||||||||||||||||
откуда |
y = e |
−∫ |
P( x)dx |
(∫Q(x)e |
∫ P( x)dx |
dx + C) – |
общее решение дифференци- |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
ального уравнения (1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Пример 3. Решить уравнение y¢ + ytgx = |
1 |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
Решение. |
|
Умножим |
|
обе |
|
части уравнения на |
|
1 |
, |
получим |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|
||
|
d y |
|
= |
|
1 |
|
|
или |
|
y |
= tgx + C , или |
y = C cos x + sin x |
– общее |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
dx cos x |
|
cos2 x |
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
решение исходного уравнения.
39
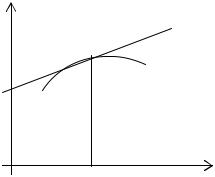
Пример 4. Найти уравнение кривой, которая проходит через точку
А(а, а) и обладает следующим свойством: |
если в любой точке |
|
М(x, y) |
|||||||||||||||||||||||||||||||||||||||
кривой с ординатой, равной BM провести касательную до пересечения |
||||||||||||||||||||||||||||||||||||||||||
с осью ординат в точке |
С, то площадь трапеции |
|
|
OCMB постоянна и |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
равна a2 (рис. 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
Решение. Площадь трапеции OCMB – |
||||||||||||||||||||||||||||||||
|
M(x,y) |
|
|
S = |
1 |
( |
|
OC |
|
+ |
|
MB |
|
)× |
|
OB |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
C |
|
|
|
|
2 |
Так как |
|
|
|
OC |
|
= y - x × y′ ; |
|
OB |
|
= x ; |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
MB |
|
|
= y , то получим дифференциальное уравне- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
= 2a |
2 |
|
|
или x |
2 |
′ |
− 2xy + 2a |
2 |
= 0 , |
||||||||||||||||||
|
|
|
|
|
ние (2 y − xy )x |
|
|
|
|
|
y |
|
|
|||||||||||||||||||||||||||||
0 |
|
B |
x |
откуда 0 = x4 × |
d |
|
|
|
|
y |
|
|
|
+ 2a |
2 . |
|
|
Интегрируя, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Рис. 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
получим y = x2 |
|
|
|
|
|
|
|
|
+ C . Так как y(a) = a, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
C = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2a2 |
|
+ |
|
x2 |
|
|
|
|
|
|||||||
тогда |
|
. Следовательно, уравнение кривой |
y |
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
3x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
3a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a |
|
|
|
|
|
||||
|
|
|
|
Уравнение Бернулли |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Дифференциальное уравнение Бернулли – |
это уравнение вида |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
y′ + P(x) y = Q(x) yn , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12) |
|||||||||||||
где |
P(x) |
и Q(x) – определенные и непрерывные функции: n – постоян- |
||||||||||||||||||||||||||||||||||||||||
ная величина (n ¹ 0; n ¹ 1). Если n = 0 или n = 1, уравнение (12) – |
|
это ли- |
||||||||||||||||||||||||||||||||||||||||
нейное уравнение или уравнение с разделяющимися переменными. Интегрирование уравнения Бернулли приводится к интегрированию
линейного дифференциального уравнения первого порядка с помощью но- вой переменной: если разделить уравнение (12) на yn, то
|
|
|
|
|
y′ |
|
+ |
P( |
x) |
= Q(x) . |
(13) |
||
|
|
|
|
|
n |
|
n |
−1 |
|||||
|
|
|
|
|
y |
|
y |
|
|
|
|
||
Положим Z = |
|
1 |
; Z ¢ = (1 - n) |
y′ |
|
||||||||
|
|
|
|
, тогда уравнение (13) |
приводим к виду |
||||||||
y |
n−1 |
y |
n |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Z ′ |
+ P(x)Z = Q(x) . |
(14) |
||||||
|
|
|
1 - n |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
40
