
14-es_1 / Высшая математика (РТФ) / умк_Цывис_Диф.уравнения_Ряды
.pdf
вует [6, С. 132, 338]. Если µ = µ(x,y) непрерывно дифференцируемая функ-
ция, тогда из тождества ¶(m × P) = |
¶(m ×Q) |
следует, |
что µ – решение сле- |
||||||||||
|
¶y |
|
|
¶x |
|
|
|
|
|
||||
дующего уравнения с частными производными |
|
|
|
||||||||||
Q ¶m - P ¶m = m ¶P - ¶Q |
. |
(13) |
|||||||||||
¶x |
¶y |
|
¶y |
¶x |
|
||||||||
Уравнение (13) имеет решение µ = µ(ω), где ω = ω(x,y), тогда находим |
|||||||||||||
¶m = |
dm |
× |
¶w; |
|
|
|
¶m = |
dm |
× ¶w |
||||
|
|
|
|||||||||||
¶x dw ¶x |
|
|
|
¶y dw ¶y |
|||||||||
и получаем: |
|
dm = m ¶P |
- ¶Q |
. |
|||||||||
Q ¶w - P ¶w |
|||||||||||||
|
|
|
|
|
|
|
|||||||
¶x |
¶y |
dw |
|
|
¶y |
¶x |
|||||||
Откуда следует, что если |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
¶P - ¶Q |
|
|
|
|
|
||||
|
|
|
|
¶y |
¶x |
|
|
|
|
|
|||
|
|
|
|
= y(w) , |
(14) |
||||||||
|
|
Q |
¶w - P ¶w |
||||||||||
|
|
|
|
¶x |
|
¶y |
|
|
|
|
|
||
то есть левая часть есть функция от ω, то существует интегрирующий множитель µ = µ(ω), который является решением уравнения
dμ = y(w) × m , dw
которое имеет вид
m = e |
∫ ψ(ω)d ω |
(c =1) . |
(15) |
|
Условие (14) – необходимое и достаточное для того, чтобы уравне- ние (1) имело бы функцию μ = μ(ω(x, y)) как интегрирующий множитель.
Если интегрирующий множитель зависит только от переменной x, то из (14) имеем
|
¶P - |
¶Q |
|
||
|
¶y |
¶x |
= y(x) |
и m = e∫ψ( x)dx . |
|
|
Q |
|
|
||
|
|
|
|
|
|
Если интегрирующий множитель зависит только от переменной y, |
|||||
то из (14) имеем |
|
|
|
|
|
|
¶P - |
¶Q |
|
||
|
¶y |
¶x |
= y( y) |
и m = e∫ψ( y)dy . |
|
|
|
|
|||
|
-P |
|
|||
51

|
|
Пример 4. |
|
Решить уравнение |
(1 − x 2 y)dx + x 2 ( y − x)dy = 0 . |
||||||||||||||||||||||||||||||||||||||
|
|
Решение. |
Это дифференциальное уравнение имеет интегрирующий |
||||||||||||||||||||||||||||||||||||||||
множитель µ, |
зависящий от x, так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂P − |
∂Q |
|
|
|
|
|
−x2 − 2xy + 3x2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
∂x |
= |
|
= − |
2 |
= ψ(x) |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 ( y − x) |
|
|
|
|
x |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∫ |
|
2 |
dx |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Поэтому |
|
|
|
|
|
|
μ = e |
|
|
|
x |
|
|
= |
|
. |
|
|
|
Следовательно, |
|
|
уравнение |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|||||||||||||||||||||
|
1 |
(1 − x2 y)dx + ( y − x)dy = 0 |
|
|
|
– |
|
уравнение в полных дифференциалах, кото- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рое проинтегрируем следующим образом |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
− ydx + ydy − xdy = 0 . |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
dx |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
||||||||
|
|
Так как |
|
|
|
|
|
|
= d |
|
− |
|
|
|
; |
|
|
|
|
ydx + xdy = d (xy); |
|
ydy = d |
|
|
|
, тогда дан- |
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ное уравнение можно записать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
y2 |
1 |
|
|
|||||||||||||
|
|
d |
|
− |
|
|
|
− d (xy) + d |
|
|
|
|
|
= 0 |
или |
|
d |
|
|
|
− xy − |
|
|
= 0 , |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
x |
|
|
||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2xy − |
2 |
|
= 0 , |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
тогда общий интеграл исходного дифференциального уравнения имеет вид
y2 − 2xy − 2 = C .
x
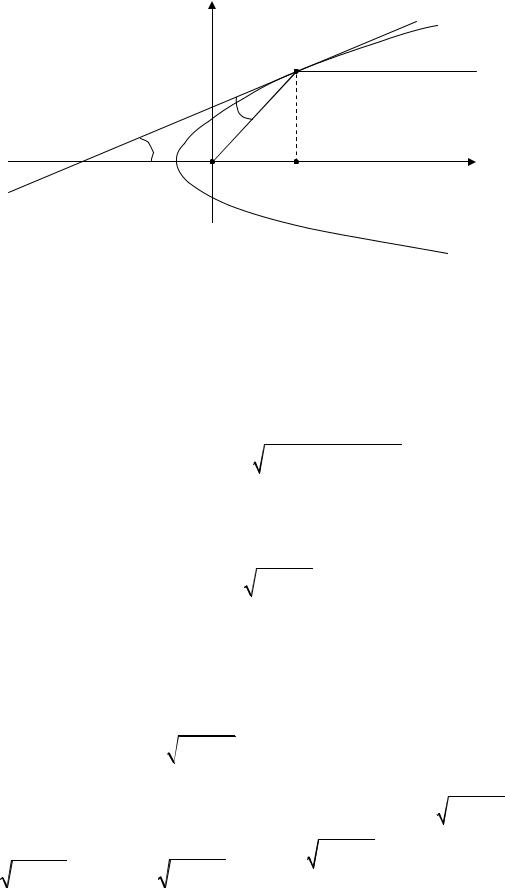
Пример 5. Определить форму зеркала, которое все лучи, выходящие из заданной точки, отражает параллельно данному направлению.
Решение. Пусть точечный источник света расположен в начале ко- ординат, ось Ox направлена параллельно данному направлению. Точка M(x,y) – произвольная точка зеркала. Рассмотрим сечение зеркала плоско- стью xOy, проходящей через точку M(x,y) и ось Ox. В полученной плос- кости в точке M(x,y) проведем касательную MN (рис. 2).
52
y
M ϕ 
ϕ
N ϕ
0 |
M1 |
x |
Рис. 2
В силу закона отражения (угол падения равен углу отражения) име-
ем, что |
NOM – равнобедренный |
(|NO| = |
|OM|). |MM1| = y; |
|OM1| = x; |
|||||||||||||||||||||||||||||||||
tgϕ = |
dy |
и из NMM1 |
имеем |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
dx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgϕ = |
|
|
|
MM1 |
|
|
= |
|
|
|
|
MM1 |
|
|
|
|
= |
|
|
|
|
|
MM1 |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
NM1 |
|
|
|
|
|
|
NO |
|
+ |
|
OM1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(OM1)2 + (MM1)2 + |
|
ОМ1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Тогда дифференциальное уравнение, описывающее формулу (y = f(x)) |
||||||||||||||||||||||||||||||||||||
сечения зеркала плоскостью xOy имеет вид |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
= |
|
|
|
y |
|
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx x + |
|
x2 + y2 |
|
|||||||||||||||
Это однородное уравнение, которое интегрируется с помощью заме-
ны y = u × x .
Проинтегрируем полученное уравнение как уравнение в полных дифференциалах, используя интегрирующий множитель. Действительно, освободившись от иррациональности после разделения переменных, полу-
чим уравнение xdx + ydy = 
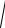 x2 + y2 dx .
x2 + y2 dx .
|
Уравнение имеет интегрирующий множитель μ(x, y) = |
|
1 |
|
, |
по- |
||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + y2 |
|
||
|
|
xdx + ydy |
|
|
d (x2 + y2 ) |
|
|
|
|
|
|
|
|
|
|
|
||||
этому |
|
− dx = 0 |
, |
− dx = 0 |
, x2 |
+ y2 |
= x + c , |
y2 = 2cx + c2 . |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
x2 + y2 |
2 x2 + y2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
53
Следовательно, сечение зеркала – парабола, а поверхность зеркала – параболоид вращения.
Замечание 3. Если m0 (x, y) – интегрирующий множитель уравнения
(1) и u0 (x, y) |
– интеграл этого же уравнения (1), тогда все интегрирующие |
||||
множители |
уравнения |
(1) |
выражаются |
формулой |
|
m(x, y) = m0 (x, y) × j(u0 (x, y)) , |
где j(t) – произвольная непрерывно диффе- |
||||
ренцируемая функция. |
|
|
|
|
|
Используя это утверждение, в ряде случаев удается найти интегри- |
|||||
рующий множитель следующим образом. |
|
|
|||
Уравнение (1) представим в виде |
|
|
|||
|
P (x, y)dx + Q (x, y)dy + P (x, y)dx + Q (x, y)dy = 0 |
||||
|
1 |
1 |
2 |
2 |
|
и пусть m1(x,y) и m2(x,y) – |
интегрирующие множители, а |
u1(x,y) и u2(x,y) – |
|||
интегралы |
соответственно |
уравнений |
P (x, y)dx + Q (x, y)dy = 0 и |
||
|
|
|
|
1 |
1 |
P2 (x, y)dx + Q2 (x, y)dy = 0 . Следовательно, |
все интегрирующие множители |
||||
первого из этих уравнений имеют вид m(x, y) = m1(x, y) × j1(u1(x, y)) , а второ-
го – m(x, y) = m2 (x, y) × j2 (u2 (x, y)) , где j1(t) и j2(t) – |
произвольные диффе- |
|
ренцируемые функции. Если существуют функции j* |
(t) и j* |
(t) такие, что |
1 |
2 |
|
m1(x, y) × j1* (u1(x, y)) = m2 (x, y) × j*2 (u2 (x, y)) ,
то m(x, y) = m1(x, y) × j1* (u1(x, y)) – интегрирующий множитель уравнения (1).
Пример 6. Решить уравнение (x3 − xy2 − y)dx + (x2 y − y3 + x)dy = 0 .
Решение. Запишем исходное уравнение в виде
x(x2 − y2 )dx + y(x2 − y2 )dy + xdy − ydx = 0 .
Рассмотрим уравнение |
|
|
x(x2 − y2 )dx + y(x2 − y2 )dy = 0 . |
(I) |
|
1 |
|
|
Его интегрирующий множитель m(x, y) = |
|
, тогда xdx + ydy = 0 |
x2 - y2 |
||
и, следовательно, x2 + y2 = c. |
|
|
Поэтому все интегрирующие множители уравнения (I) выражаются формулой
m (x, y) = |
|
1 |
j(x2 |
+ y2 ) , |
|
|
|||
1 |
x2 |
- y2 |
|
|
|
|
|
где j(t) – произвольная дифференцируемая функция.
54

|
|
Уравнение |
|
|
|
|
||
|
|
xdy – ydx = 0 |
|
|
|
(II) |
||
имеет интегрирующий множитель μ(x, y) = |
1 |
, значит |
dy |
− |
dx |
= c , т.е. |
||
|
|
|
||||||
|
|
|
xy |
y x |
||||
|
y |
= c . |
|
|
|
|
||
|
|
|
|
|
|
|||
|
x |
|
|
|
|
|||
Поэтому все интегрирующие множители уравнения (II) определяют- ся формулой
μ2 (x, y) = 1 ϕ2 (x, y) , xy
где ϕ2 (t) – произвольная дифференцируемая функция.
Так как, ϕ1(t) и ϕ2 (t) – произвольные функции, подберем их так,
чтобы было справедливо равенство |
|
|
1 |
|
|
|
ϕ (x2 |
+ y2 ) = |
1 |
|
ϕ |
|
y |
. |
|||||||||||||||||||
|
x2 − y2 |
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
xy |
x |
||||||||||||||
Последнее имеет место, когда |
|
ϕ1(t) = 1, |
ϕ2 (t) = |
t |
. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 − t2 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Выбрав указанным образом функции |
|
ϕ1(t) |
и ϕ2 (t) , найдем интег- |
||||||||||||||||||||||||||||||
рирующий множитель исходного уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m(x, y) = m1(x, y) = |
|
|
= m2 (x, y) = |
|
|
|
|
x |
|
|
|
. |
|
|
|
|||||||||||||||||
|
|
x2 - y2 |
|
xy |
y |
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
- |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||
Умножая обе части исходного уравнения на m(x, y) = |
|
|
1 |
|
, полу- |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
x2 - y2 |
|||||||||||||||||||||||||||||||||
чим уравнение в полных дифференциалах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
y |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x - |
|
|
dx + y + |
|
|
|
|
|
dy |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x2 |
- y2 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
- y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x - y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решая его, получим |
x2 + y2 - ln |
|
= 2c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x + y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Замечание 4. |
Уравнение |
|
с |
разделяющимися |
|
|
|
переменными |
|||||||||||||||||||||||||
M (x) × N ( y)dx + M1(x)N1( y)dy = 0 |
имеет |
интегрирующий |
множитель |
||||||||||||||||||||||||||||||
m(x, y) = |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
N ( y) × M1(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55

Замечание 5. |
Однородное уравнение |
P(x, y)dx + Q(x, y)dy = 0 име- |
|||||||||||
ет интегрирующий множитель m(x, y) = |
|
|
1 |
, |
P × x + Q × y ¹ 0 . |
||||||||
|
|
|
|||||||||||
P × x |
|
||||||||||||
|
|
|
|
|
|
|
|
+ Q × y |
|
|
|||
Замечание 6. |
Линейное уравнение |
y′ + P(x) y = Q(x) имеет интегри- |
|||||||||||
рующий |
множитель |
m(x) = e |
∫ P( x)dx |
, |
а |
уравнение |
Бернулли |
||||||
|
|
||||||||||||
y¢ + P(x) y = Q(x) y |
n |
– M (x) = y |
−n |
× e |
(1−n)∫ P( x)dx |
. |
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
2.6. Уравнение Лагранжа и Клеро
Уравнение Лагранжа и Клеро являются дифференциальными урав- нениями типа y = ϕ(x, y′) или x = ψ( y, y′) , неразрешенными относитель-
но производной искомой функции.
Уравнение Лагранжа. Уравнение Лагранжа имеет вид
|
|
|
|
|
|
′ |
|
|
|
|
|
′ |
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
y = xf ( y ) |
+ g( y ) , |
|
|
|
|
|
|
||||||||
где |
′ |
′ |
известные функции от |
y |
′ |
. |
|
|
|
|
|
|
||||||||
f ( y ) и |
g( y ) – |
|
|
|
|
|
|
|
||||||||||||
|
Дифференциальное уравнение (1) интегрируется с помощью подста- |
|||||||||||||||||||
новки |
|
|
|
|
|
y′ = p , |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|||||
где |
p – параметр. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда уравнение (1) имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
y = f ( p)x + g( p) . |
|
|
|
|
|
|
|
|
(3) |
||||||
|
Дифференцируя (3) по переменной x, |
|
получим |
|
||||||||||||||||
|
|
|
dy |
= f ( p) + xf ¢( p) |
dp |
+ g¢( p) |
dp |
, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
dx |
|
|
|
dx |
|
|
|
|
|
dx |
|
||||||
то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p - f ( p) = [xf ¢( p) + g¢( p)] |
dp |
|
|
||||||||||||||
|
|
|
dx |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
или |
|
|
|
|
|
′ |
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
- x |
f ( p) |
= |
|
|
g ( p) |
. |
(4) |
|||||||||
|
|
|
|
dp |
p - f ( p) |
p |
|
|||||||||||||
|
|
|
|
|
|
|
- f ( p) |
|
||||||||||||
Это линейное дифференциальное уравнение относительно искомой функции x, общее решение которого
f ′( p)dp x = e∫ p− f ( p)
|
g¢( p) |
−∫ |
f ′( p)dp |
p − f ( p) |
|||
C + ∫ |
|
e |
|
p - f ( p) |
|
||
|
|
|
dp . (5)
56

Исключая из общего решения (5) и дифференциального уравнения
(4) p, получим общее решение уравнения (1).
Если уравнение p − f ( p) = 0 имеет действительные решения p = pi
(i = 1, n) , то, подставляя их в дифференциальное уравнение (1) и учитывая,
что |
f ( pi ) = pi , |
получим |
y = pi x + g( pi ) . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6) |
|||||||||||
|
Эти прямые могут быть особыми решениями дифференциального |
||||||||||||||||||||||||||
уравнения (1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. Решить уравнение y |
′ |
|
|
|
|
′ |
2 |
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
+ y = x( y ) |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Решение. |
Решим это уравнение относительно y: |
|
|
′ 2 |
− y |
′ |
– это |
|||||||||||||||||||
|
y = x( y ) |
|
|||||||||||||||||||||||||
уравнение Лагранжа. Поэтому |
|
p = y′ , |
|
тогда |
y = xp2 − p . Дифференцируя |
||||||||||||||||||||||
по |
x, получим |
|
dy |
= p2 + 2 px |
dp |
− |
dp |
|
|
|
или |
p = p2 + 2 px |
dp |
− |
dp |
, откуда |
|||||||||||
|
|
|
|
dx |
|
|
|
|
|
||||||||||||||||||
|
|
|
dx |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
dx dx |
|
|
||||||||
имеем линейное уравнение |
dx |
+ |
2 |
|
|
|
x = |
|
1 |
|
|
; |
решая его, |
|
находим |
||||||||||||
|
p −1 |
p( p − |
1) |
|
|||||||||||||||||||||||
|
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
||||||||||||
x = p − ln p + c . ( p −1)2
Уравнение Клеро. Частным случаем уравнения Лагранжа является уравнение Клеро, которое имеет вид
|
|
|
|
|
|
y = xy |
′ |
|
′ |
|
(7) |
|||
|
|
|
|
|
|
|
+ g( y ) . |
|
||||||
Уравнение Клеро (7) отличается от уравнения Лагранжа (1) тем, что |
||||||||||||||
коэффициент при x |
в уравнении Клеро равен y′ , а в уравнении Лагранжа |
|||||||||||||
коэффициент при x – |
функция от |
y′ . |
|
|
|
|
||||||||
Для решения (7) положим |
y′ = p , тогда уравнение (7) примет вид |
|||||||||||||
|
|
|
|
|
|
y = xp + g( p) . |
|
(8) |
||||||
Дифференцируя по x уравнение (8), получим |
|
|
||||||||||||
|
|
|
|
dp |
′ |
|
dp |
|
|
′ |
dp |
|
||
|
p = p + x |
|
+ g ( p) |
|
|
|
|
или |
(x + g ( p)) |
|
= 0 . |
|||
dx |
dx |
|
dx |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Если |
dp |
= 0 , |
то p = c, |
тогда с учетом (8), уравнение (7) имеет об- |
||||||||||
|
||||||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
щее решение |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y = x × c + g(c) . |
|
(9) |
||||||
57

Уравнение |
′ |
образуют систему уравнений |
x + g ( p) = 0 и уравнение (8) |
||
|
x + g¢( p) = 0, |
(10) |
|
|
|
|
y = xp + g( p). |
|
Исключая из этой системы p, находим особое решение. |
||
Пример 2. |
Решить уравнение y × ( y¢)2 + 2xy¢ - y¢ = 0 . |
|
Решение. |
Это уравнение можно решить как уравнение Лагранжа. В |
|
этом случае решим уравнение проще, применяя подстановку t = y2 . Тогда
t′ = 2 yy′ , |
|
следовательно, |
исходное |
уравнение |
примет |
|
вид |
|||
′ |
2 |
+ 4xt |
′ |
- 4t = 0 , т.е. исходное уравнение – уравнение Клеро. Решая его, |
||||||
(t ) |
|
|
||||||||
найдем t = -x2 и t = Cx + |
c2 |
, но так как |
t = y2 , то имеем |
y2 = cx + |
c2 |
. |
||||
|
4 |
|||||||||
|
|
|
|
4 |
|
|
|
|
||
Задачи для самостоятельной работы
1. Найти общее решение уравнения
1.1) 2xydx + (x2 − y2 )dy = 0 .
Ответ: 3x2 y − y3 = C .
1.2) (2 − 9xy2 )xdx + (4 y2 − 6x3 ) ydy = 0 .
Ответ: x2 − 3x3 y2 + y4 = C . 1.3) e− ydx − (2 y + xe− y )dy = 0 .
Ответ: xe− y − y2 = C .
1.4) x dx + ( y2 + ln x)dy = 0 . y
|
Ответ: 4 y ln x + y4 = C . |
||||||||||
1.5) |
(2x − y + 1)dx + (2 y − x −1)dy = 0 . |
||||||||||
|
Ответ: x2 |
+ y2 − xy + x − y = C . |
|||||||||
|
|
y |
|
y |
|||||||
|
(x + e |
|
)dx + e |
|
(1 − |
x |
)dy = 0 y(0) = 2 . |
||||
1.6) |
x |
x |
|||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
y |
||
|
|
|
|
|
|
|
x |
||||
|
|
|
|||||||||
|
Ответ: x2 |
+ 2 ye |
y |
= 4 . |
|||||||
58

2. Найти общее решение дифференциальных уравнений имеющих интег- рирующий множитель
2.1) (2x − y3 ) − 3y2dy = 0 . x
Ответ: x2 − xy3 = C . 2.2) ydx + (x + x2 y2 )dy = 0 .
Ответ: xy2 −1 = Cxy . 2.3) (x2 + y)dx − xdy = 0 .
Ответ: x − y = C . x
2.4) ( y − 1 )dx + dy = 0 . x y
Ответ: (x2 − C) y = 2x .
2.5) (x3 + xy2 )dx + (x2 y + y3 )dy = 0 .
Ответ: (x2 + y2 )2 = C . 2.6) x sin xdx + cos2 ydy = 0 .
Ответ: 4sin x − 4x cos x + 2 y + sin 2 y = 0 . 2.7) (x2 + y)dx − xdy = 0 .
Ответ: x − y = C . x
3. Найти кривую, у которой отрезок касательной в любой точке кривой, заключенный между точкой касания и осью абсцисс, равен расстоянию от точки пересечения касательной с осью абсцисс до точки А(0;а).
Ответ: 2xydx + ( y2 − x2 − a2 )dy = 0 ; μ( y) = |
1 |
; x2 + y2 + a2 − Cy = 0 . |
|
y2 |
|||
|
|
4. Проинтегрировать дифференциальные уравнения Лагранжа и Клеро.
4.1) |
2 |
+ 4). |
|
|
2 yy '= x ((y ') |
|
|
||
|
Ответ: y = Cx2 + |
1 |
; y = ±2x . |
|
|
|
|||
|
|
|
C |
|
4.2) |
2 |
|
|
|
y + xy '= (y ') . |
||||
Ответ: x = C − p ; y = −xp + p2 . p
59

4.3) |
y = y( y ')2 + 2xy . |
|
|
|
|
|
|
|
|||||||||||
|
Ответ: 3Cx = C 2 − y2 . |
|
|
|
|
|
|
||||||||||||
4.4) |
y = 2 y 'x + |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
y ' |
|
|
|
|
|
|
|
||||||||
|
Ответ: x = |
1 |
(ln p + C) ; |
y = 2 px + |
1 |
. |
|||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
p2 |
|
|
|
|
|
p |
|||||||
|
y = y '+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4.5) |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
1− (y ') . |
|
|
|
|
|
|
|
||||||||||||
|
|
x = ln |
|
p |
|
− arcsin p + C |
|||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Ответ: |
|
|
|
|
|
|
|
|||||||||||
|
1 − p |
|
|
|
|
|
|
||||||||||||
|
|
y = p + |
2 . |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y = xy '+ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
4.6) |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
1+ (y ') . |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||||
|
Ответ: y = Cx + |
1 + C 2 ; |
x2 + y2 = 1. |
||||||||||||||||
4.7) |
xy '− y = ln y . |
|
|
|
|
|
|
|
|||||||||||
|
Ответ: y = Cx − ln C ; |
y = ln x + 1. |
|||||||||||||||||
5. Найти кривую, касательные к которой отсекают на осях координат от- резки, сумма длин которых равна 2а.
Ответ: y = xy '+ 2ay ' ; ( y − x − 2a)2 = 8ax . y '− 1
6. Найти кривую, проходящую через начало координат и такую, что отре- зок нормали к ней, отсекаемый сторонами первого координатного угла, имеет постоянную длину, равную 2.
|
|
p( p |
2 |
+ 2) |
|
|
|
|
|
p |
2 |
|
|
|
|||
x = |
|
, |
x = |
|
|
|
, |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
( p2 + 1)3 |
( p2 + 1)3 |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
Ответ: |
|
|
p2 |
|
|
|
|
2 p2 + 1 |
|
|
|||||||
|
y = |
|
|
. |
|
y = |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
( p2 + 1)3 |
( p2 + 1)3 |
||||||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||
7. Найти кривую, касательная к которой образует с осями координат тре-
угольник площадью 2a2 .
Ответ: y = xy '+ 2a
 − y '; xy = a2 .
− y '; xy = a2 .
60
