Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Неопределенный интеграл

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

2.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 176 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Рис. 3

Замечая, что

= 2 , и придавая k

указанные значения, находим

шесть корней уравнения:

= 2 cos

+ i sin

= 3 + i ,

= 2 cos

+ i sin

= -

3 + i ,

= 2

cos p

+ i sin p

= 2i ,

= 2

cos

+ i sin

= -

- i ,

= 2

+ i sin

= -2i ,

cos

= 2

cos

11p

+ i sin

11p

- i .

Эти корни уравнения можно изо- бразить вершинами правильного шес- тиугольника, вписанного в окружность радиуса R = 664 = 2 , (рис. 3).

Полученные корни можно изо- бразить и другим способом: изобража- ется число z0 , а затем, разбивая окруж-

ность на шесть равных частей, опреде- ляются остальные пять корней.

Показательная форма комплексного числа

Для получения комплексного числа в показательной форме восполь- зуемся формулой Эйлера, устанавливающей связь между показательной и тригонометрической функциями:

			eiϕ = cos j + i sin j.
Показательной формой комплексного числа z = x + iy называют
выражение вида			z = r × eiϕ ,
где r =	z	, а j –	аргумент комплексного числа z.

Функция eiϕ			обладает свойствами показательной функции с дейст-

вительным показателем, поэтому формулы умножения, деления, возведе- ния в натуральную степень для комплексных чисел в показательной форме имеют простой вид.

Если	z	= r × eiϕ1	,	z	2	= r × eiϕ2	,		то z			× z	2	= r × r × ei(ϕ1 + ϕ2 ) .
	1	1			2	2					1		2			1		2
								z		r × eiϕ1							r		i(ϕ −ϕ		)
	z2 ¹ 0 ,							1	=	1					=	1		× e	i(ϕ −ϕ		)	.
Если						то													1	2
Если						то		z2		r	× eiϕ2						r2		1	2
								z2		r	× eiϕ2						r2
										2

Если

n Î N ,

z = r × eiϕ ,

то zn = (r × eiϕ )n = r n × einϕ .

i×j+2kp

zk =

r × e

× e

, k

= 0, n -1.

Основные задачи на комплексные числа

Пример 1. Найдите сумму, разность, произведение и частное чисел z1 = 4 + 5i и z2 = 2 - 6i .

Решение.

z1 + z2 = (4 + 5i) + (2 - 6i) = 6 - i ;

z1 - z2 = (4 + 5i) - (2 - 6i) = 2 + 11i ;

z1 × z2 = (4 + 5i)(2 - 6i) = 38 -14i ;

4 + 5i

(4 + 5i)(2 + 6i)

= -

i .

2 - 6i

(2 - 6i)(2 + 6i)

Пример 2. Определить действительную и мнимую часть числа:

2.1) z = −5 + 11i ;

2.3) z =

1 + 6i

;

3 + i

2.2) z = (7 + 2i)(1 − 3i) ;

2.4) z-1 , если

z = 2 − 7i .

Решение.

2.1)

Re z = −5 ,

Imz = 11;

2.2) так как

z = (7 + 2i)(1 - 3i) = 7 - 21i + 2i - 6i2 =

= (7 + 6) + (2 - 21)i =13 -19i , то

Re z = 13 ,

Imz = −19 ;

2.3) так как

z =

1 + 6i

(1 + 6i)(3 − i)

3 + 17i − 6i2

= ,

+ i

+ i)(3 − i)

9 − i2

9 + 17i

i , то Re z =

Imz =

;

2.4) в силу того, что

z-1 =

(2 + 7i)

− 7i

(2 − 7i)(2 + 7i)

z 2

2 + 7i

i , тогда

Re z =

, Imz =

4 - 49i2

Пример 3.

Вычислить z2 , если z = −5 + 2i .

Решение.

(-5 + 2i)2 = (-5)2 + 2(-5) × (2i) + (2i)2 = 25 - 20i + 4i2 = 21 - 20i .

Пример 4. Вычислить 22 + 22i .

Решение. Запишем число

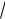22 + 22i = 4(cos π + i sin π) .

			4		4
Отсюда имеем

4		π	+ i sin	π
4	cos		+ i sin		= 2 cos
		4		4

22 + 22i в тригонометрической форме

π	+ 2kπ		π
4	+ 2kπ	+ i sin	4	+ 2kπ
4			4		, где k = 0,1.
	2			2	, где k = 0,1.
	2			2

Тогда при k = 0

получим

= 2

, при k = 1

получим

cos

+ i sin

= 2

cos

9π

+ i sin

9π

Пример 5. Вычислить

−16

Решение. Так как

−16 = 16(cos π + i sin π) , то

π + 2kπ

4 −16 = 4

+ i sin

, k = 0,3 .

cos

Полагая последовательно k = 0, 1, 2, 3 и учитывая, что 4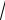16 = 2 , по- лучим четыре значения корня 4-й степени из числа – 16, которые распола-

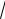гаются в вершинах квадрата, вписанного в окружность радиуса R = 664 = 2 : z0 = 2 + 2i; z1 = −2 + 2i; z2 = −2 − 2i; z3 = 2 − 2i .

Пример 6. Решить уравнение:

6.1)	x2	− 3x + 10 = 0;	6.3)	x4	− 5x2 − 6 = 0;
6.2)	x3	− 4x2 + 6x − 4 = 0;	6.4)	x4	− 37 = 0 .

Решение. 6.1) Используя формулу решения квадратного уравнения, получим

	=	3 ±			=	3 ±		i	=	3	±
x			−31				31						31	i .

1,2	2			2			2					2

6.2) Заданное уравнение кубическое, поэтому оно имеет по крайней мере один действительный корень. И в первую очередь рассмотрим дели- тели свободного члена (т. к. целые корни многочлена с целыми коэффици-

ентами являются делителями свободного члена). Среди делителей ± 1, ± 2,

± 4 методом подбора устанавливаем, что число x = 2 – корень данного уравнения. Разделим многочлен x3 – 4 x2 + 6x – 4 на многочлен (x – 2):

_x3 – 4 x2 + 6x – 4

x – 2

x3 – 2 x2

x2 – 2 x + 2

_– 2x2 + 6x – 4

– 2 x2 + 4x

_2x – 4

2x – 4

Значит, имеет место равенство:

x3 − 4x2 + 6x − 4 = (x − 2)(x2 − 2x + 2) .

Тогда корни исходного уравнения:

x = 2,

2 ± 2i

=1 ± i .

2,3

6.3) Заменой

y = x2 приводим

исходное

уравнение к

виду

y2 - 5 y - 6 = 0 . Корнями

полученного

квадратного уравнения

будут

y1 = −1;

y2 = 6 . Отсюда корнями исходного уравнения будут числа

x1 =

x2 = -

x3 = i;

x4 = -i .

6.4) Первый способ. Аргумент действительного числа равен нулю,

поэтому

arg 37 = 0;

= 37 . Исходное уравнение запишем в виде

x4 = 37 .

kπi

Откуда x = 4

× e

, k =

0,3

Таким образом, данное уравнение имеет четыре корня:

πi

eπi = - 4

3πi

x = 4

37;

x = 4

37e 2

= 4

x = 4

;

x = 4

37e 2

= - 4

Второй способ. Левую часть заданного уравнения разложим на мно- жители: (x2 - 437 )(x2 + 437 ) = 0 .

Отсюда получим два квадратичных уравнения:

(x2 - 4

) = 0, (x2 + 4

) = 0 .

= 4

= - 4

, а из вто-

Из первого уравнения будем иметь x

37;

= 4

x = - 4

рого будем иметь x

37i.

Замечание. В общем случае решение алгебраического уравнения

степени n > 2 с комплексными коэффициентами

a xn + a

n−1

xn−1 + ... + a x + a = 0,

a ¹ 0,

n Î N

является очень сложной задачей. Но вопрос о существовании корней этого уравнения решает основная теорема алгебры.

ТЕОРЕМА. Каждое алгебраическое уравнение в множестве комплексных чисел имеет хотя бы один корень.

	Опираясь на данную теорему, доказано, что левую часть уравнения
a xn + a		xn −1 + ... + a x + a			= 0,	a ¹ 0, n Î N можно представить в ви-
n	n −1		1	0		n
де произведения				a (x − x )m1		(x − x )m2	...(x − x )mk ,
				n	1	2	k
где	х1, х2,…, хk, –		корни уравнения; m1, m2,…,				mk N и m1 + m2 + … +	mk = n.
	В этом случае говорят, что число х1 является корнем кратности m1,
х2 –	корнем кратности			m2	и т. д. Тогда имеет место следующая теорема
(корень уравнения будем считать столько раз, какова его кратность):
	ТЕОРЕМА.		Каждое алгебраическое уравнение степени n					имеет
в множестве комплексных чисел ровно n корней.

Напомним, что функция называется рациональной, если она не со- держит действия извлечения корня (возведения в дробную степень). Такую функцию принято обозначать R(x) – символ рациональной зависимости. Различают целую рациональную функцию – многочлен и дробно- рациональную функцию – отношение двух многочленов, т. е.


R ( x) =	Q	( x)	=	b xm + b xm −1		+ …+ b
	m			0	1	m
							.
	Pn	( x)		a0 xn + a1xn −1 + …+ an

Если m < n , то дробь называется правильной, в противном случае − неправильной. Неправильную дробь всегда можно представить в виде суммы целой части (многочлена) и правильной дроби. Это можно сделать посредством деления числителя на знаменатель столбиком.

x3 + 2x2

Пример 1.

Неправильную дробь

(в числителе многочлен

x2 −

третьей степени, в знаменателе –

второй) представить в виде суммы целой

части и правильной дроби.

x3 + 2x2

x2 – 3

x3 – 3 x

x + 2

2x2 + 3x

2x2 – 6

3x + 6

+ 2x2

3x + 6

В результате получим

= x + 2 +

− 3

x2 − 3

Здесь целая часть – ( x + 2), правильная дробь − 3x + 6 . x2 − 3

Существует общий метод разложения правильной рациональной дроби на сумму простейших дробей.

К ним относятся правильные рациональные дроби вида:

(I) ( ) ; x − a

		A
(II)			, (k ³ 2,				k Î N) ;
	( x - a)k
		Mx + N			( D = p2 - 4q < 0) ;
(III)				,

		x2 + px + q
(IV)		Mx + N				,	(k ³ 2, D = p2 - 4q < 0),

		(x2 + px + q)k

где A, a, M, N, p, q – действительные числа.

Каждая правильная дробь может быть представлена в виде суммы простейших дробей указанных четырех типов. Для разложения правильной

Q ( x)

рациональной дроби ( ) на простейшие дроби, нужно:

P x

а) разложить знаменатель P(x) на линейные и квадратичные множи-

тели:

P ( x) = ( x - a)m ×... × ( x - b)k × (x2 + px + g )n ×... × (x2 + cx + d )r ;

б) написать схему разложения данной дроби на простейшие дроби в следующем виде:

Q ( x)

+ …+

P ( x)

x - a

( x - a)2

( x - a)m

x - b

( x - b)2

( x - b)k

M1x + N1

M 2 x + N2

M n x + Nn

+ …+

x2 + px + g

(x2 + px + g )2

(x2 + px + g )n

C1x + D1

C2 x + D2

+ …+

Cr x + Dr

x2 + cx + d

(x2 + cx + d )2

(x2 + cx + d )r

где

A1, …,

B1, …, M1, …,

N1, …, C1, …,

D1, …,

Dr - некоторые неизвест-

ные коэффициенты.

В эту схему для каждого множителя в разложении знаменателя P(x) вписывается столько простейших дробей, какова его кратность (m, k, n, r).

Знаменателями простейших дробей являются все целые степени ка- ждого множителя в разложении P(x), начиная с первой степени и кончая той степенью, которую множитель имеет в разложении P(x).

Числителями простейших дробей служат либо постоянные A1, A2, … либо линейные функции M1x + N1 , … смотря по тому, является ли знаме-

натель дроби некоторой степенью линейной или квадратичной функции; в) правую часть разложения нужно привести к общему знаменателю

и выполнить действие сложения; г) знаменатели левой и правой частей равенства равны, значит,

должны быть тождественно равными и их числители;

д) коэффициенты A1, A2, …, B1, B2, … находятся с помощью метода неопределенных коэффициентов или метода частных значений (иногда комбинируют оба метода).

1. Провести краткий теоретический обзор по теме « Комплексные числа». Выделить три формы комплексного числа, обратить внимание на геометрическую интерпретацию комплексного числа. Решить следующий пример (преподаватель у доски):

Даны числа z1 = 5 − 7i,

− 2i

1) Записать числа в тригонометрической и показательной формах,

изобразить их на плоскости.

2) Вычислить: а) 4z - 7z

× z

z −1

;

б)

; в)

; г)

;

д) 3 z

z4 = 47 ;

2. Студент у доски решает уравнения: а)

б)

1 − i

3. Преподаватель у доски показывает разложение рациональной дро-

би

7x3 + 3x + 3

на простейшие рациональные дроби.

x3 − 3x2 − 18x

4. Студент

доски

раскладывает

на

простейшие

рациональную

дробь:

3x + 5

(

x2 + 2x + 7

)(

)

x2 − 2x + 1

Домашнее задание

1.Подготовить теоретический материал по теме «Таблица интегра- лов. Непосредственное интегрирование. Метод подведения под знак диф- ференциала».

2.Выполнить свой вариант из индивидуального домашнего задания.

Индивидуальные домашние задания

Вариант 1

1. Решить уравнение

2x2 − 5x + 4 = 0.

= −2

2. Записать числа z

= 5 − 7i,

тригонометрической и

1 − i

показательной формах, изобразить их на плоскости.

Вычислить: а) 5z - 3z

; б) z

× z

;

в)

;

г)

z −1 ; д)

3 z

3.Решить уравнение: z4 = 26.

4.Представить рациональную дробь в виде суммы простейших ра- циональных дробей:

2x + 7

5x3 − 4x + 3

а)

;

б)

(3x2 + 2)( x − 5)

x3 − 4x2 + 3x

Вариант 2

Решить уравнение

3x2 − 4x + 7 = 0.

Записать числа

= 5 − 7i,

2 2

в тригонометрической и

1 − i

показательной формах, изобразить их на плоскости.

Вычислить: а) 5z - 3z

; б) z × z

;

в)

;

г) z −1 ; д)

3 z

3.Решить уравнение z4 = 21.

4.Представить рациональную дробь в виде суммы простейших ра- циональных дробей:

2x + 3

7x3 − 5x + 6

а)

;

б)

(x2 + 7)( x − 4)

x3 − 5x2 + 6x

Вариант 3

Решить уравнение

3x2 − 5x + 9 = 0.

Записать числа z1

= 3 − 4i,

в тригонометрической и

−

показательной формах, изобразить их на плоскости.

Вычислить: а) 5z - 3z

; б) z

× z

; в)

; г) z −1

; д)

3 z

Решить уравнение

z4 = 16.

4. Представить рациональную дробь в виде суммы простейших ра- циональных дробей:

2x + 3

4x3

− 3x − 4

а)

;

б)

(

)

( x − 9)

+ 1

x − 3x

− 4x

Вариант 4

Решить уравнение

3x2 − 5x + 7 = 0.

−4

Записать числа z

= 4 − 5i,

в тригонометрической и

3 − i

показательной формах, изобразить их на плоскости.

Вычислить: а) 5z - 3z

; б) z

× z

;

в)

;

г)

z −1

; д)

3 z

3.Решить уравнение z4 = 9.

4.Представить рациональную дробь в виде суммы простейших ра- циональных дробей:

5x + 8

3x3 − 5x − 6

а)

;

б)

(3x2 + 2)( x − 5)

x3 − 5x2 − 6x

Вариант 6

Решить уравнение

4x2 − 5x + 7 = 0.

Записать числа z

= 3 − 4i,

−1

в тригонометрической и

3 − i

показательной формах, изобразить их на плоскости.

Вычислить: а) 5z - 3z

; б) z

× z

;

в)

;

г) z −1 ; д)

3 z

3.Решить уравнение z4 = 30.

4.Представить рациональную дробь в виде суммы простейших ра- циональных дробей:

	3x + 7					2x3 − 4x + 3
а)		;		б)					.
	(x2 + 2)( x − 3)					x3 + 4x2 + 3x
			Вариант 7
1.	Решить уравнение		4x2 − 5x + 7 = 0.
			= 4 − 5i, z = −2					в тригонометрической и
2.	Записать числа z						2
	1		2		1 − i

показательной формах, изобразить их на плоскости.

Вычислить: а) 5z - 3z

× z

; г) z −1

; б) z

; в)

;

д) 3 z

3.Решить уравнение z4 = 22.

4.Представить рациональную дробь в виде суммы простейших ра- циональных дробей:

3x + 1

3x3 − 7x + 12

а)

;

б)

(7x2 + 2)( x − 3)

x3 − 7x2 + 12x

Вариант 8

Решить уравнение

3x2 − 5x + 9 = 0.

Записать числа z1

= 3 − 5i,

z2 =

в тригонометрической и

3i − 1

показательной формах, изобразить их на плоскости.

Вычислить: а) 5z - 3z

; б) z

× z

; в)

; г) z −1

; д)

3 z

3.Решить уравнение z4 = 28.

4.Представить рациональную дробь в виде суммы простейших ра- циональных дробей:

7x + 2

5x3 − 8x + 7

а)

;

б)

(3x2 + 4)( x − 2)

x3 − 8x2 + 7x

Вариант 9

Решить уравнение

2x2 − 7x + 9 = 0.

Записать числа z1

= 9 − 4i,

в тригонометрической и

3 + 1

показательной формах, изобразить их на плоскости.

Вычислить: а) 5z - 3z

; б) z

× z

; в)

; г) z −1

; д)

3 z

3.Решить уравнение z4 = 25.

4.Представить рациональную дробь в виде суммы простейших ра- циональных дробей:

а)				3x + 7	;	б)	5x3	− 10x + 9	.
а)	(		2	)	;	б)	3	2	.
		4x	2	+ 1 ( x − 5)			3	2
		4x		+ 1 ( x − 5)			x − 10x + 9x
							x − 10x + 9x

<<< < Предыдущая 1 2 3 4 56 / 176 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб41умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf