Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Неопределенный интеграл

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

2.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1716 17 > Следующая >>>

	Пример 6.	Найти	∫x cos(x + 5)dx .
	Решение. Применим метод интегрирования по частям:
			∫udv = uv - ∫vdu
∫		u = x; du = u 'dx = x 'dx = dx						=
	x cos(x + 5)dx =			∫	dv =	∫		=
				∫		∫
		dv = cos( x + 5)dx;v =					cos( x + 5)dx = sin ( x + 5)

= x ×sin ( x + 5) - ∫sin ( x + 5) dx =x ×sin ( x + 5) + cos( x + 5) + C .

Пример 7.					Найти					∫	xdx					.


											9 - x2
Решение.				Воспользуемся методом подведения под знак дифферен-
циала: ∫			xdx		=		2		∫	xdx			= -		1			∫	-2xdx					= -		1	∫	d (9 - x2 )				=
			xdx				2			xdx					1				-2xdx							1

			9 - x2							9 - x2										9 - x2									9 - x2
			9 - x2			2				9 - x2		2								9 - x2				2					9 - x2
																							1										1
								1										(9 - x2 )−						+1							(9 - x		2 )
						−		1															2	+1										2
= -	1	∫(9 - x2 )				−		2 d (9 - x2 ) = -						1											+ C = -					1				2	+ C =
= -		∫(9 - x2 )						2 d (9 - x2 ) = -													1				+ C = -							1			+ C =
2												2					-				1	+1						2				1
																	-				2	+1										2
																					2											2

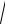= −9 − x2 + C .

Найти ∫

cos3 xdx

Пример 8.

sin

cos3 xdx

cos2 x × cos x

1 - sin2 x

Решение.

∫

= ∫

dx = ∫

cos xdx =

(поделим

sin

−

sin2 x

числитель

на

знаменатель

почленно)

cos xdx

∫

sin

t = sin x, dt = cos xdx

∫

− 1 cos xdx = (введём замену переменной) =

sin2 x

dx =

cos x

t−2+1

t−1

= ∫

− 1 cos x

= ∫

− ∫dt =

− t + C = =

− t + C =

cos x

−2 + 1

−1

= −

− t + C = (вернёмся к старой переменной) = −

− sin x + C .

sin x

151

Пример 9.

Найти ∫

5 − 3x

dx .

5 − 3x

4 - 3x2

Решение.

∫

dx = ∫

dx - ∫

dx = (во втором ин-

4 - 3x2

теграле воспользуемся методом подведения под знак дифференциала)

= ∫		5					dx -			2		∫			3x							dx = ∫			5				dx +			1	∫				−6x		dx =
										2																						2
			4 - 3x2																							4 - 3x2
			4 - 3x2												4 - 3x2											4 - 3x2										4 - 3x2
= 5∫			dx			+		1	∫	d		(4 - 3x2 )								=			5	∫			dx					+		1	∫		d (4 - 3x2 )				=
			dx					1															5				dx							1


				2		2												2												2			2							2
		4 - 3x		2		2						4		- 3x				2					3		22 - (			3x)		2			2			4 -		3x		2
		4 - 3x										4		- 3x									3		22 - (			3x)								4 -		3x
																				1
											1 (4 - 3x2 )
																					2
	5					3																			5					3
=	5	arcsin				3		x	+														+ C =		5		arcsin			3	x		+				4 - 3x2 + C .
=		arcsin			2			x	+		2					1							+ C =				arcsin				x		+				4 - 3x2 + C .
	3				2						2					1									3			2
														2
Пример 10.							Найти						∫						2 − x						dx .

															4x		2		+16x -12
															4x				+16x -12

Решение. Выделим полный квадрат в знаменателе подынтегральной функции:

4x2 +16x -12 = 4(x2 + 4x - 3) = 4((( x)2 + 2 × x × 2 + 4)- 4 - 3) = 4(( x + 2)2 - 7).

			∫				2 − x								dx = ∫													2 − x													1				∫				2 − x
																						4(( x + 2)2 - 7)																	dx =																	dx =
					4x2 +16x -12																	4(( x + 2)2 - 7)																	dx =		4					( x + 2)2 - 7										dx =
	1	∫		2								1		∫							x												1		∫					dx										1		∫		2( x + 2) - 4
=									dx -																				dx =																			-												dx =
=	4		( x +	2)		2	-	7	dx -			4				( x +				2)				2	- 7				dx =				2					( x +		2)			2		- 7			-		8				( x +			2)	2	- 7	dx =
	4		( x +	2)			-	7				4				( x +				2)					- 7								2					( x +		2)					- 7					8				( x +			2)		- 7
						1	∫			dx								-		1			∫			2( x + 2)												dx +		1		∫							dx						=

						2		( x +		2)			2	- 7						8					( x +					2)		2	- 7							2					( x +				2)		2		- 7
						2		( x +		2)				- 7						8					( x +					2)			- 7							2					( x +				2)				- 7
									= ∫										dx												-	1		∫		d (( x + 2)2 - 7)															=

																													2															2
											( x			+ 2)					2	- (					7 )				2			8						( x + 2)						2		- 7
											( x			+ 2)						- (					7 )													( x + 2)								- 7

																			+	2 -
																	x															1	ln				x2 + 4x - 3										+ C .
										1				ln													7			-
										1																	7

								2				7							7		+ x + 2											8
								2				7							7		+ x + 2											8

152

					Неопределенные интегралы
					(повышенный уровень)
			2 + 3x2		15.	∫	x cos x
1. ∫			x2 (1 + x2 )	dx				dx
1. ∫			x2 (1 + x2 )	dx			sin3 x	dx
2. ∫			dx		16.	Ιn = ∫(4 − x2 )n dx
	1	+ e5x			16.	Ιn = ∫(4 − x2 )n dx

x2 −1

3. ∫ (x4 + 3x2 + 1)arctg x2 + 1dx x

4. ∫ 1 − x2 dx x4

5. ∫ 1 + ln x dx

3 + x ln x

6.	∫		x5		dx

		1 − x2
		1 − x2
	∫cos5 x
7.	∫cos5 x			sin xdx

8. ∫ x2 31 − xdx

9. ∫e5x cos 4xdx

10. ∫cos(ln x)dx

11. ∫ x ln(1 + 1 )dx x

12.∫ln(1 − x + 1 + x )dx

13.∫sin x ln tg xdx

14.∫ln(x + 1 + x2 )dx

17.Ιn = ∫(ln x)n dx

18.Ιn = ∫ sindxn x

Ι= xndx

19.n ∫ x2 + a

20.Ιn = ∫tgn xdx

x4dx

21.∫ (2 + x)(x2 −1)

2x2 − 3x + 3 22. ∫ x3 − 2x2 + 3 dx

23. ∫ (x2 + 1)(x2 + 4)

24. ∫ 5x3 + 9x2 − 22x − 8 dx x2 − 4x

25. ∫ x + 3 x2 + 6 x dx x(1 + 3 x )

22 − x

26.∫ (2 − x)2 3 2 + x dx

27. ∫ (1 − x)1 − x2

28. ∫1 + x2 + 2x + 2

153

29. ∫

(1 + x)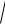1 + x − x2

30. ∫ (x + 1 + x2 )5 dx 1 + x2

5x + 4

31. ∫ x2 + 2x + 5 dx

32. ∫ cos3 x dx sin6 x

33. ∫ dx cos4 x

34. ∫ sin4 x dx cos x

35. ∫ sin x(2 + cos x − 2sin x)

36. ∫ sin2 x cos x dx sin x + cos x

37. ∫

cos4 x sin2 x

ln x 38. ∫ dx

39. ∫e− x ln(1 + cx )dx

154

1.∫5sin x × x15dx;

2.∫e11x × tg xdx;

∫

;

4x2 + 2x -10

∫

dx;

+ x6

∫

+ 4x -15

;

+ x -10x

- 2

dx ;

∫

x - 3

2x -14

∫

+ 5

dx ;

∫(3x2 +1)cos(x)dx ;

∫

8x2

dx ;

- 4x + 3

10.∫ ln(x)dx ;

ЗАДАНИЯ

11.	∫		x4	- 4		dx ;
		x2	-
				5x + 6
12.	∫	4arctg( x) dx			;
		1 + x2

13.∫(x2 - 2x + 3)sin(x)dx ;

14.∫ e5 arcsin( x)dx ;

1 - x2

15.

∫

+ 3

x2 +

2x + 5

∫

e−4 x

16.

dx ;

−4x

+ 2

17.

∫(x4 - 2)sin2 (x)dx ;

dx ;

18.

∫

4 2x

∫

x4 - 6x + 5

19.

dx ;

+ 6

20.

∫

ln2 (x)dx

x4 +1

Вам необходимо выполнить задания самостоятельно с помощью приведенных в приложении программ и представить отчёт об их вы- полнении.

155

ГЛОССАРИЙ

Первообразной для	называется функция F ( x) , которая является
функции f(x) на некото-	дифференцируемой и для которой для любо-
ром множестве X	го x X выполняется равенство
		F′( x) = f ( x)			или	dF ( x) = F′( x) × dx

Неопределённым	называется множество					всех первообразных
Неопределённым	для функции f ( x)
интегралом	для функции f ( x)

Интегрируемой на [a, b]	называется функция, для которой на						[a,b]
	существует первообразная, а значит, и неоп-
	ределённый интеграл

Интегрированием	называется			операция		нахождения	не-
Интегрированием
	определённого интеграла

Свойство			′
Свойство	если F (x) = f (x) , то ∫ f (u)du = F (u) + C;
инвариантности	где u = j( x) –			произвольная функция, имею-
	где u = j( x) –			произвольная функция, имею-
	щая непрерывную производную

Непосредственное	выполняется с помощью таблиц, преобразо-
Непосредственное	вания подынтегральных выражений, свойств
интегрирование	вания подынтегральных выражений, свойств
интегрирование
	неопределенного интеграла

Метод поднесения под	основывается			на	свойстве инвариантности
знак дифференциала	неопределенного					интеграла:	если
знак дифференциала	′				∫ f (u)du = F (u) + C
	′
	F ( x) = f ( x) , то
Чтобы поднести под	нужно записать под знаком дифференциала
Чтобы поднести под
знак дифференциала	ее первообразную
знак дифференциала
функцию

Метод замены	заключается во введении новой переменной с
Метод замены
переменной	целью получения табличного интеграла или
переменной	интеграла, сводимого к табличным
	интеграла, сводимого к табличным

Интегрирование вы-	выделением полного квадрата из квадратного
ражений, содержащих	трёхчлена и введением замены переменной
квадратный трёхчлен	x +	b	= t интегралы сводятся к табличным
квадратный трёхчлен	x +		= t интегралы сводятся к табличным
		2a
	или к более простым

Метод интегрирова-	∫udϑ = uϑ − ∫ϑdu
ния по частям

156

Циклическое

применяя формулу интегрирования по час-

тям достаточное число раз (но не менее

интегрирование

двух), получают в правой части равенства

интеграл, аналогичный интегралу в левой

части равенства. Решая полученные уравне-

ния относительно искомого, получают дан-

ный интеграл

Простейшие

правильные рациональные дроби вида

рациональные дроби I,

(I)

;

II, III и IV типов

( x - a )

(II)

, (k ³ 2, k Î N) ;

( x - a )k

(III)

Mx + N

, ( D = p2 - 4q < 0);

x2 + px + q

(IV)

Mx + N

(k ³ 2, D = p2 - 4q < 0),

(x2 + px + q)k

где A, a, M, N, p, q –

действительные числа

Алгоритм

если дробь неправильная, то, разделив

числитель на знаменатель, нужно отделить

интегрирования

рациональных дробей

целую часть и правильную рациональную

дробь;

2) в правильной рациональной дроби знаме-

натель нужно разложить на множители;

3) правильную рациональную дробь предста-

вить в виде суммы простейших рациональ-

ных дробей;

4) проинтегрировать целый многочлен и сум-

му простейших рациональных дробей

Интегрирование

ax + b

иррациональных

∫ R

,...,

dx =

= t

функций

cx + d

p = НОК (n1, n2 ,..., nk )

Дифференциальным

+ bx

)

называется выражение

где m,

биномом

n, p, – рациональные числа;

a, b –

действи-

тельные числа

157

Интегрирование

выражаются через элементарные функции в

следующих трёх случаях:

дифференциальных

целое(

);

биномов

p –

a + bx = t

m + 1

a + bxn = t q ,

–

целое

;

q − знаменатель( p)

m + 1

a + bxn = t q xn ,

+ p

–

целое

q − знаменатель( p)

Интегрирование

всегда может быть выполнено с помощью

тригонометрической под-

тригонометрических

универсальной

функций

становки

= t, x = 2arctg t,

dx =

+ t2

sin x =

cos x =

1 − t2

, tg x =

1+ t2

1 + t2

− t2

158

ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА

1.Бабко, Г.И. Учебно-методический комплекс: теория и практика проек- тирования (Методические рекомендации для преподавателей вузов) / Г.И. Бабко. – Минск: РИВШ, 2004.

2.Беспалько, В.П. Системно-методическое обеспечение учебно- воспитательного процесса подготовки специалистов / В.П. Беспалько,

Ю.Г. Татур. – М., 1989.

3.Вакульчик, В.С. Элементы линейной алгебры. Введение в математи- ческий анализ. Дифференциальное исчисление функции одной пере- менной: учеб.-метод. комплекс / В.С. Вакульчик. – Новополоцк: ПГУ, 2007.

4.Высшая математика: учеб.-метод. комплекс для студентов техн. спец. В 2-х ч. Ч. 1 / сост. и общ. ред. Н.В. Цывиса. – Новополоцк: ПГУ, 2004. – 264 с.

5.Гусак, А.А. Справочник по высшей математике / А.А. Гусак, Г.М. Гу- сак. – Минск: Навука и тэхника, 1991.

6.Гусак, А.А. Высшая математика: учеб. для студентов вузов. В 2 т. Т. 1 / А.А. Гусак. – 5- е изд. – Минск: ТетраСистемс, 2004.

7.Данко, П.Е. Высшая математика в упражнениях и задачах. В 3 ч. Ч. 1 / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высш. шк., 1980.

8.Зайцев, И.А. Высшая математика: учеб. для неинженерных специально- стей с.-х. вузов / И.А. Зайцев. – М.: Высш. шк., 1991.

9.Зуев, Д.Д. Повышение эффективности учебно-методического ком- плекса как средств интенсификации учебно-воспитательного процес- са: Проблемы школьного учебника / Д.Д. Зуев. – М.: Просвещение, 1987.

10.Жевняк, Р.М. Высшая математика. В 2 ч. Ч. 1 / Р.М. Жевняк, А.А. Карпук. − Минск: Выш. шк., 1985.

11.Мышкис, А.Д. Лекции по высшей математике / А.Д. Мышкис. – М.:

Наука, 1973.

12.Пальчевский, Б.В. Концепция УМК / Б.В. Пальчевский, Л.С. Фрид- ман. − Минск, 1993.

13.Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. – 2- е изд., исп. – М.: Айрис-пресс, 2002.

14.Проектирование и разработка учебно-методических комплексов по циклу социально-гуманитарных дисциплин в вузе. Материалы для

159

слушателей курсов повышения квалификации / под общ. ред. А.В. Макарова − Минск: РИВШ, 2003.

15.Сборник задач по математике для втузов: спец. разделы математиче- ского анализа / под ред. А.В. Ефимова и Б.П. Демидовича. − М.: Нау-

ка, 1981.

16.Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа / под ред. А.В. Ефимова, Б.П. Демидовича. –

М.: Наука, 1986.

17.Сборник индивидуальных заданий по высшей математике. Ч. 1, Ч. 2 / под общ. ред. А.П. Рябушко. − Минск: Выш. шк., 1991.

18.Сергеенкова, В.В. Управляемая самостоятельная работа студентов. Модульно-рейтиноговая и рейтинговая системы / В.В. Сергеенкова. −

Минск: РИВШ, 2000.

19.Столяр, А.А. Педагогика математики: учеб. пособие для физ.-мат. фак. пед. ин-тов / А.А. Столяр. − Минск: Выш. шк., 1986.

20.Яско, Ф.Ф. Методические рекомендации о порядке разработки, ут- верждения и распространения учебно-методических комплексов / Ф.Ф. Яско. – Новополоцк: ПГУ, 2004.

21.Яско, Ф.Ф. Положение о подготовке и выпуске научных и учебных изданий / Ф.Ф. Яско. – Новополоцк: ПГУ, 2005.

160

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1716 17 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб41умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf