Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Вакульчик_Неопределенный интеграл

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

2.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 174 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

6.10. Интегрирование правильной рациональной дроби

ТЕОРЕМА 6.10.1 (основная теорема алгебры). Всякий многочлен n-

ной степени (n > 0) имеет по крайней мере один корень, действительный или комплексный.

ТЕОРЕМА 6.10.2. Всякий многочлен n-ой степени можно предста-

вить в виде	Pn ( x) = a0 ( x - x1 )( x - x2 )...( x - xn ) ,
где x1, x2 ,..., xn –	корни многочлена, a0 – коэффициент многочлена при
старшей степени.

ТЕОРЕМА 6.10.3. Всякий многочлен n-ной степени с действитель- ными коэффициентами можно разложить на линейные и квадратичные множители с действительными коэффициентами:

Pn ( x) = a0 ( x - x1 )k1 ( x - x2 )k2 ...( x - xs )ks ´ ´(x2 + p1x + q1x)l1 ...(x2 + pm x + qm x)lm .

При этом k1 + k2 + ... + ks + 2(l1 + l2 + ... + lm ) = n , а квадратичные трехчлены не имеют действительных корней.

Определение 6.10.1. Рациональной дробью или дробно-рациональ- ной функцией называется функция, равная отношению двух многочленов:

f ( x) = Qr ( x) . Pn ( x)

Определение 6.10.2. Рациональная дробь называется правильной,

если степень числителя меньше степени знаменателя, в противном случае рациональная дробь называется неправильной.

Определение 6.10.3. Правильные рациональные дроби вида

	A
(I)		;
(I)	( x - a)	;
(II)	A		,	(k ³ 2, k Î N) ;

	( x - a)k
	( x - a)k
(III)	Mx + N				,	( D = p2 - 4q < 0);
(III)					,	( D = p2 - 4q < 0);
	x2 + px + q
(IV)	Mx + N						, (k ³ 2, D = p2	- 4q < 0),
(IV)	(x2 + px + q)k						, (k ³ 2, D = p2	- 4q < 0),
	(x2 + px + q)k

где A, a, M, N, p, q – действительные числа, называются простейшими

рациональными дробями I, II, III и IV типов.

ТЕОРЕМА 6.10.4. Пусть дана правильная рациональная дробь

( x)

где все коэффициенты –

действительные числа,

причем числитель и зна-

менатель не имеют одинаковых множителей.

Пусть знаменатель разложен на множители

Pn ( x) = a0 ( x − x1 )k1 ...( x − xs )ks × (x2 + p1x + q1x)...(x2 + pm x + qm x)lm .

Тогда дробь можно представить (единственным образом) в виде

суммы простейших рациональных дробей:

Qr ( x)

Ak1

Bks

... +

+ ... +

Pn ( x)

( x − x1 )

( x − x

)k1

( x − xs )

( x − x

)ks

x + N

C x + D

x + Dl

+ (x2 + p1x + q1 ) + ... + (x2 + pm x + q m ) + ... +

(6.10.1)

(x2 + pm x + q m )lm

где A1,..., Ak

, B1,..., Bk

M1, N1,...,C1, D1,...,Cl , Dl

– некоторые действи-

тельные коэффициенты.

Замечание 6.10.1. Коэффициенты в формуле (6.10.1) могут быть найдены следующим образом: правую часть разложения нужно привести к общему знаменателю; знаменатели левой и правой частей формулы будут одинаковые, значит, должны быть тождественно равны числители. При- равнивая коэффициенты при одинаковых степенях x слева и справа, полу- чим столько уравнений, сколько неизвестных коэффициентов. Решив по- лученную систему, найдем эти коэффициенты.

Замечание 6.10.2. Если в знаменателе имеются действительные различные корни, то можно придать x значения действительных корней в тождестве числителей. Тем самым, также будет получено соответствую- щее количество уравнений. Для получения необходимой системы уравне- ний для подстановки в тождество числителей значений x можно использо- вать и другие числа.

Замечание 6.10.3. Простейшие дроби I, II типов интегрируются подведением под знак дифференциала; интегрирование простейших дро- бей III и IV было рассмотрено в п. 6.6.

Алгоритм интегрирования рациональных дробей:

1) если дробь неправильная, то, разделив числитель на знаменатель, нужно отделить целую часть и правильную рациональную дробь;

2)в правильной рациональной дроби знаменатель нужно разложить на множители;

3)правильную рациональную дробь представить в виде суммы про- стейших рациональных дробей;

4)проинтегрировать целый многочлен и сумму простейших рацио- нальных дробей.

Пример 1.

∫

x4 + 2x3 + x2 + 3x + 1

dx =

∫( x + 2)dx + ∫

x + 1

dx.

x3 + x

x + 1

Bx + C

x (x2 + 1)

x2 + 1

x + 1 = A(x2 + 1) + x ( Bx + C ).

Приравнивая коэффициенты при одинаковых степенях x, будем иметь

A = 1.

0 = A + B B = − A, B = −1.

C = 1.

Тогда заданный интеграл приводится к сумме:

−x + 1

xdx

+ 2x +

∫

dx =

2x + ln

− ∫

+ ∫

2 + 1

2 +

x2 + 1

d (x2 + 1)

ln (x

+ 1) + arctg x + C.

+ 2x + ln

−

∫

+ arctg x

+ 2x + ln

−

x2 + 1

6.11. Интегрирование иррациональных функций

Определение 6.11.1. Функция, содержащая в своем аналитическом выражении радикалы, называется иррациональной.

Замечание 6.11.1. Не от всякой иррациональной функции инте- гралы выражаются через элементарные функции.

В тоже время интеграл от рациональной функции можно всегда представить в виде суммы элементарных функций.

Рассмотрим те иррациональные функции, для которых интегралы с помощью соответствующих подстановок сводятся к интегралам от рацио- нальных функций.

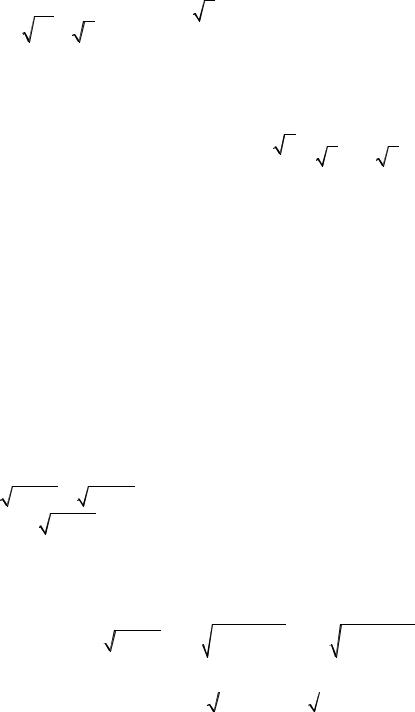
	m1		m2		mk		, dx = pt p −1dt
1. ∫R x, x	n1	, x n2		,..., x nk dx =		x = t p	, dx = pt p −1dt	,

где

p = НОК (n1, n2 ,..., nk ) ; R(x) –

рациональная функция.

Пример 1.

∫

x = t6 ; t = 6

; dx = 6t5dt

= ∫

6t5dt

= 6∫

dt =

t4 − t3

t3 (t −1)

3 x2 −

(t2 −1) + 1

(t + 1)dt + ∫

d (t −1)

= 6∫

dt = 6∫

= 6

∫

t −1

−1)

−1

+ t + ln

t −

+ C = 6

+ 6 x

+ ln

6 x −

+ C .

ax + b

∫R

,...,

+ d

ax + b

= t p , ax + b = t p (cx + d ) ,

x (a − ct p ) = dt p − b;

cx + d

= ∫R1 (t )dt ,

x =

dt p

− b

dt p − b

′

; dx

a − ct

где

p = НОК (n1, n2 ,..., nk ) ; R1(x) –

рациональная функция.

Пример 2.

+ 3

t12 − 3

2x + 3

∫

2x + 3 = t

; x =

; dx =

12t dt =

6t dt

4 2x + 3

∫

(

)

∫(

)

+ t4

t15

t13

6t dt =

6 t

+ t

dt =6 t

+ t

dt =

+ C =

t = 12

(2x + 3)15

(2x + 3)13

2x + 3

= (2x + 3)

4 2x + 3 +

12 2x

+ 3

+ C .

Пример 3.

∫

= ∫

1 + x

dx .

(1 - x

)

1 + x (1 - x )

1 - x

= t,

1 + x

= t2 , 1 + x = t2 - t2 x, x (1 + t2 ) = t2 -1, x =

t 2 -1

Введем замену:

1 + x

1 - x

t 2 +1

-1

′

(

t 2

+1 - 2t

(

t 2

-1

2 × 2tdt

dx =

dt =

)

dt =

(t 2 +1)

(t2 +1)

(t2 -1)2

(t 2

+1)2 - (t2 -1)2

2t2 × 2

1 - x

=1 -

(t2 +1)2 =

(t 2 +1)2

dt .

(t 2 +1)2

Заданный интеграл приводится к табличному:

(t2 +1)2

1 + x

∫

× (1 - x2 ) dx

= ∫t ×

4t 2

dt = ∫dt

= t + C =

+ C.

1 - x

(t 2 +1)2

1 - x

6.12. Интегрирование дифференциальных биномов

Определение 6.12.1.

Дифференциальным биномом называется вы-

ражение xm (a + bxn )p , где m, n, p –

рациональные числа; a, b – действи-

тельные числа.

ТЕОРЕМА 6.12.1 (Чебышева).

Интеграл от дифференциального би-

нома

∫ xm (a + bxn )p dx

выражается через элементарные функции в сле-

дующих трёх случаях:

1)р - целое число a + bxn = z ;

2)m + 1 - целое число a + bxn = zq , где q - знаменатель р; n

m +1

a + bx

= z

× x

+ p

- целое число

, где q - знаменатель р.

∫ dx = ∫ −1 ( + 5 )−1

Пример. x 1 x 3 dx x × 3 1 + x5

Для подынтегральной функции выполняется условие m + 1 = 0 . В со- n

ответствии с Т.6.12.1 введем замену:

												1 + x5 = t3, x5 = t3 -1,
																										1																					4														.
												x = (t3 -1)																, dx =								1			(t3 -1)−													×3t 2dt
																										5										1														5
																										5										5														5
Заданный интеграл принимает вид
									4									1
	3	∫t 2 ×(t3 -1)−								×(t3 -1)−													×t −1dt =												3			∫t (t3 -1)−1 dt =																					3			∫		t		dt =
	3								5												5														3																								3					t
	5								5												5														5																								5					t3 -1
=							t										=					A				+				Bt + C												=		1							1				-				(t -1)								=
							t															A								Bt + C														1							1								(t -1)

			(t -1) ×(t 2						+ t +1)										t -1										t2 + t +1															3							-		1					2 + t +
			(t -1) ×(t 2						+ t +1)										t -1										t2 + t +1															3			t				-		1				t	2 + t +							1
																																														1														1
			1			d (t -1)						- ∫							(t -1)																						t +					1		= y, y -												1			= t,		=
			1			d (t -1)													(t -1)																						t +							= y, y -															= t,
			=		∫																													dt					=					2														2
			=		∫	t -1																				2								dt					=					2														2
			5			t -1										t +						1						+			3										dt = dy
																						1									3


																						2							4
																																		y -					3
														1
																																							2
																ln				t -1							- ∫												2				dy =
												5				ln				t -1							- ∫						y2				+						dy =
												5																												3

																																							4
																									2			+	3
				1											1			d y																					3			2												2 y
																		d y											4
			=		ln		t -1				-						∫																		-										arctg														+ C =

																													3
				5									2									y		2		+													2			3													3
				5									2											2															2			3													3
																													4


					1										1									2					3										3										2t +1
					1										1									2					3										3										2t +1
				=		ln		t -1					-				ln y									+						+										arctg														+ C =
				=		ln		t -1					-				ln y									+						+										arctg														+ C =
					5										2														4										3														3
					5										2														4										3														3

										2					3			5
										2					3			5
=	1	ln	3	1 + x5	-1	-	1	ln	(3 1 + x5 )	+ 3 1 + x5 +1	+	3	arctg	2		1	+ x		+1	+ C.
			3

5						2											3

6.13. Интегрирование тригонометрических функций

ТЕОРЕМА 6.13.1. Интеграл ∫R (sin x,cos x)dx всегда может быть

представлен в виде элементарных функций с помощью универсальной тригонометрической подстановки, где R(x) – рациональная функция.

= t,

x = 2arc tg t,

− t2

sin x =

, cos x =

, tg x =

(*)

1 + t2

− t 2

dx =

1 + t 2

Доказательство. Применим подстановку (*), получим

∫

R (sin x,cos x)dx =

∫

1 − t2

2dt

∫ 1

R (t)dt ,

+ t2

1 + t 2

1 + t2

где подынтегральная функция представляет собой некоторую рациональ- ную функцию относительно переменной t.

Поскольку рациональная дробь может быть проинтегрирована через рациональные функции, то интеграл от тригонометрической функции в конечном итоге будет выражен через элементарные функции.

Пример 1.

= t, x = 2arctg t,

∫

= ∫

21 + t2

= ∫

= ln

+ C.

sin x

dx =

dt, sin x =

1 + t2

Частные случаи

1. ∫sin2m x cos2n xdx,

n N

sin2 x =

1 - cos 2x

;cos2 x =

1 + cos 2x

;sin x × cos x =

sin 2x

– понижаем степень.

2.1.

∫ R (sin x,cos x)dx .

if R (−sin x,cos x) = −R (sin x,cos x) – sin

x в нечетной степени, то подво-

дим под знак дифференциала функцию sin x или вводим замену cos x = t:

sin xdx = −d cos x,

или cos x = t,

sin2 x = 1 − cos2 x dt = −sin xdx

2.2. ∫ R(sin x,cos x)dx

if R (sin x, − cos x) = −R (sin x,cos x) – cos x в нечетной степени, то подво-

дим под знак дифференциала функцию cos x или вводим замену sin x = t :

	cos xdx = d sin x,	cos2 x = 1 − sin	2 x	.
	или sin x = t,	dt = cos xdx

3. ∫R(sin x,cos x)dx .
if R (−sin x, − cos x) = R (sin x,cos x)		– функция четна относительно cos x,

sin x одновременно, то будет эффективной одна из замен:

а) если в знаменателе преобладает степень cos x:

tg x = t,

x = arc tg t, dx =

dt,

1 + t 2

;

sin x =

, cos x =

;

1 + t 2

1 + t2

б) если в знаменателе преобладает sin x:

c tg x = t,

x = arcctg t,

dx = −

dt,

1 + t2

sin x =

,cos x =

1 + t 2

1 + t2

Замечание.

В интегралах вида ∫

, где m ≥ 1 и нечётные, выгодно использо-

sin

вать универсальную тригонометрическую подстановку tg x = t . 2

Пример:

= t, x

= 2arctg t,

2dt

(1 + t2 )2

1 + t 2

∫

= ∫

∫

dt =

sin3 x

dx =

2dt

,sin x =

(2t )3

1 + t

(

+ t 2

)

1 + 2t2 + t 4

∫t −3dt + 2∫

1 t −2

t 2

∫

dt =

+ ∫tdt

+ 2ln

+ C =

−2

= −

tg2

+ C .

2 x

Если же в знаменателе находится cos x в нечётной степени, то эта подстановка становится не выгодной. В этом случае выгоднее использо- вать замену sin x = t :

cos xdx

d sin x

∫

= ∫

sin x = t

= ∫

;

cos3 x

cos4 x

(1 - sin2 x)2

(1 + t )2 (1 - t )2

(1 + t )

(1 + t )2

(1 - t )

(1 - t )2

Сравним с выражением

= t, x

= 2arctg t,

2dt

(1 + t 2 )2

1 + t

∫

= ∫

= 2∫ (1 - t 2 )3 dt

cos3 x

dx =

2dt

,cos x =

1 - t 2

(1 - t2 )3

1 + t 2

(1 + t2 )2

(1 + t2 )3

(1 + t )3 (1 - t )3

(1 + t )

(1 + t )2

(1 + t )3

(1 - t )

(1 - t )2

(1 - t )3

cos (m - n) x - cos(m + n) x

4.1.

∫

sin mx ×sin nxdx =

sin mx ×sin nx =

;

(m - n) x + sin (m + n) x

4.2.

∫

sin mx × cos nxdx =

sin mx × cos nx =

sin

;

cos(m - n) x + cos(m + n) x

4.3.

∫

cos mx × cos nxdx =

cos mx × cos nx =

Пример 1.

= t, x = 2arc tg t,

∫

= ∫

1 + t

+ cos x

dt,cos x =

1 - t

1 - t2

3 +

1 + t 2

1 + t2

= 2∫

∫

(

)

- t 2

2t2 + 4

2 t2 + 2

1 + t

3 + 3t 2 +

1 + t

arctg

+ C =

arctg

+ C .

Пример 2.

∫

= ∫

cos2 x

= ∫

d tg x

sin2 x

- 2sin x cos x + 3cos2 x

tg2 x - 2 tg x + 3

d (t −1)

t −1

tg x −1

= ∫

(t2 - 2t +1) + 2

= ∫

arctg

+ C =

arctg

+ C

(t -1)2 + 2

Пример 3.

= -∫ (1 - cos2 x)d cos x =

∫

sin3 xdx

cos4 x

= -∫

d cos x

+ ∫

cos2 xd cos x

= -

+ C.

3cos3 x

cos4 x

cos x

Пример 4.

∫

sin2 x × cos2 x

Первый способ:

∫

4dx

= - 2ctg 2x + C ;

sin 2x

Второй способ:

Третий способ:

ввести замену

tg x = t

;

d ctg x = -∫(1 + ctg−2 x)d ctg x

-∫

= -ctg x +

+ C = -ctg x + tg x + C ;

cos2 x

ctg x

Четвертый способ:

sin2 x + cos2 x

∫

dx = ∫

dx = tg x - ctg x + C .

sin2 x × cos2 x

cos2 x

sin2 x

6.14. Интегрирование выражений, содержащих квадратный трёхчлен, с помощью тригонометрических подстановок

Рассмотрим интеграл

∫R(x, ax2 + bx + c )dx ,

(6.14.1)

где R(x) – рациональная функция.

<<< < Предыдущая 1 2 34 / 174 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20152.77 Mб51умк_Вакульчик_Неопределенный интеграл.pdf
#
18.05.20153.63 Mб42умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб41умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб46умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб47умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб53умк_Пальчик_Теория вероятностей.pdf