Алгебра 3 семестр Лекцииi

ТЕОРЕМА (Евклид). НОД любых двух не равных одновременно нулю чисел a и b существует.

ДОКАЗАТЕЛЬСТВО. Так как числа a, b входят в условие равноправно, то, не уменьшая общности рассуждений, можно

разделим на полученный остаток и далее аналогично по принципу: на каждом шаге делим делитель на остаток из предыдущего деления. В результате получим соотношения:

a = bq1 + r1, 0 £ r1 < b ;

b = r1q2 + r2, 0 £ r2 < r1 ;

r1 = r2q3 + r3, 0 £ r3 < r2; K

Данный алгоритм называется алгоритмом Евклида.

1) Алгоритм Евклида обрывается.

Действительно, последовательность остатков удовлетворяет следующему свойству:

b > r1 > r2 > r3 > K ³ 0 .

Эта последовательность не может быть бесконечной, т.к. между числами b и 0 лишь конечное количество различных

натуральных чисел. С другой стороны, алгоритм оборвётся только в том случае, если его следующий шаг невозможно выполнить, а это, в свою очередь, произойдёт только тогда, когда получится нулевой остаток, на который делить нельзя. В результате, получим следующий набор условий.

a = bq1 + r1, 0 < r1 < b ;

b = r1q2 + r2, 0 < r2 < r1 ;

11

r1 = r2q3 + r3, 0 < r3 < r2;

rn −2 = rn −1qn + rn , 0 < rn < rn −1;

rn −1 = rnqn +1 + 0 .

K = НОД(rn −2, rn −1 ) = НОД(rn −1, rn ) = rn .

СЛЕДСТВИЕ. НОД двух не делящихся друг на друга чисел равен последнему ненулевому остатку в алгоритме Евклида для этих чисел.

ТЕОРЕМА (тождество Безу). Для любых двух не равных одновременно нулю чисел a и b существуют такие целые числа u,v , что

и выразим в каждом равенстве остатки.

12

В первом равенстве остаток r1 выражается в виде линейной комбинации чисел a, b . Если подставить эту

линейную комбинацию во второе равенство и привести подобные, то остаток r2 представится в виде линейной

комбинации чисел a, b . Если полученные представления для r1 и r2 подставить в третье равенство и привести подобные члены, то в виде линейной комбинации чисел a, b будет представлен остаток r3 . Продолжая этот процесс, мы в

конечном счёте получим представление в виде линейной комбинации a, b остатка rn = НОД(a, b) , т.е. найдём такие числа u,v , что

au + bv = НОД(a, b) .

ПРИМЕР. Найти НОД(13, 5) и составить для чисел 13 и 5 тождество Безу.

Применяем алгоритм Евклида к числам 13 и 5.

13 = 5 × 2 + 3 ,

5 = 3 ×1 + 2 ,

3 = 2 ×1 +1,

2 = 1× 2 + 0 .

Получилось, что НОД(13, 5) = 1. Далее выражаем из

полученных равенств остатки и подставляем их так, как описано в доказательстве теоремы. Чтобы числа не перепутались, всё, кроме частных, обозначим буквами.

13

r1 = a - 2b, r2 = b - r1 = b - (a - 2b) = -a + 3b ,

r3 = r1 - r2 = (a - 2b) - (-a + 3b) = 2a - 5b .

В результате получилось, что

НОД(13, 5) = 1 = a × 2 + b × (-5) = 13 × 2 + 5(-5) .

ТЕОРЕМА (основное свойство НОД). НОД двух не равных одновременно нулю чисел – это наибольший по абсолютной величине натуральный общий делитель этих чисел.

В одну сторону ДОКАЗАТЕЛЬСТВО сделано в замечании в начале параграфа.

Из определения НОД следует, что mMk . По свойству делимости 7 из этого получаем m = m ³ k = k . В результате k = m .

При изучении делимости большую роль играет свойство взаимной простоты чисел.

ОПРЕДЕЛЕНИЕ. Числа a и b называются взаимно простыми, если их наибольший общий делитель равен 1, т.е. числа не имеют других общих делителей кроме ±1 .

ТЕОРЕМА (признак взаимной простоты). числа a и b

взаимно просты тогда и только тогда, когда существуют такие u, v ¢ , что au + bv = 1.

14

ДОКАЗАТЕЛЬСТВО. Пусть au + bv = 1. Если число k делит числа a и b , то k делит и au + bv = 1. Делителями 1 являются

После этого можно воспользоваться признаком.

Докажем два очень важных свойства делимости, в которых используется свойство взаимной простоты.

8)Если abMc и числа a и c взаимно просты, то bMc .

9)Если a Mb, aMc и числа b, c взаимно просты, то a Mbc .

Так как по условию abMc , то левая, а, значит, и правая части равенства делятся на c .

9) Из первых двух условий следует, что существуют такие q1, q2 , что

a = bq1 = cq2 .

Правая часть равенства делится на c , следовательно bq1Mc . Так как b, c взаимно просты, то по предыдущему свойству q1Mc , следовательно,

15

q1 = cq3 .

Подставляя это выражение в первое равенство,

получаем

a = bq1 = bcq3 Þ a Mbc .

§3. Простые числа

В этом параграфе будет рассматриваться разложение на сомножители и свойство быть делителем. Чтобы не возиться со знаками, мы ограничимся случаем натуральных чисел.

ОПРЕДЕЛЕНИЕ. Натуральное число p называется

простым, если оно больше 1 и не имеет других (натуральных) делителей кроме p и 1. В противном случае оно называется

составным.

ЗАМЕЧАНИЕ. Всякое число n делится на n и на 1. Это – так называемые тривиальные делители. Очевидно,

нетривиальный натуральный делитель d должен удовлетворять неравенству 1 < d < n .

Простое число не имеет нетривиальных делителей. Если число n составное, то оно имеет нетривиальный делитель d :

n Md, 1 < d < n .

В этом случае n = d q и q также будет нетривиальным делителем числа n , т.к. если q = 1, то d = n , если q = n , то

d= 1, что невозможно по условию.

Врезультате число n является составным тогда и только тогда, когда существуют d, q такие, что

n = d q, 1 < d < n, 1 < q < n .

Часть неравенств можно опустить, например: число n

является составным тогда и только тогда, когда

16

n = d q, 1 < d, 1 < q Û n = d q, d < n, q < n .

Это связано с тем, что q = 1 Û d = n , и наоборот: q = n Û d = 1.

Докажем некоторые СВОЙСТВА ПРОСТЫХ ЧИСЕЛ.

1) Всякое натуральное число n и простое число p либо

a Mp , то a и p – взаимно просты и по свойству делимости 8 получаем, что bM p .

Это свойство можно доказать для произвольного количества сомножителей: если произведение натуральных чисел делится на простое число, то хотя бы один из сомножителей делится на это простое число.

2) (о существовании наименьшего простого делителя).

Всякое натуральное число n > 1 имеет наименьший натуральный делитель, который является простым числом.

ДОКАЗАТЕЛЬСТВО. Рассмотрим все натуральные числа, большие 1 и меньшие n . Их конечное число. Начнём подряд проверять, делят ли они число n . Если делитель найдётся, то он будет простым, т.к. в противном случае его нетривиальный делитель будет меньшим делителем данного числа. Если – нет,

17

то число не имеет нетривиальных делителей, является

простым и само будет своим наименьшим простым делителем.

СЛЕДСТВИЕ 1. Число n является составным тогда и только тогда, когда оно имеет простой делитель, удовлетворяющий условию p £ n .

ДОКАЗАТЕЛЬСТВО. Пусть n = d q, 1 < d < n, 1 < q < n . Не

уменьшая общности можно считать, что d £ q . Тогда имеем

dd £ qd = n Þ d £ n .

Любой простой делитель p числа d будет делителем n и будет удовлетворять условию p £ n .

Если число имеет простой делитель p £ n , то этот делитель будет нетривиальным, т.к.

1 < p £ n < n ,

следовательно число n является составным.

СЛЕДСТВИЕ 2. Число n является простым тогда и только тогда, когда оно не имеет простых делителей, удовлетворяющих условию p £ n .

Следствие 2 является контрапозицией к следствию 1.

СЛЕДСТВИЕ 3 (Решето Эратосфена). Если в натуральном ряду зачеркнуть числа, кратные первым k простым числам 2, 3, 5,..., pk , то все оставшиеся незачёркнутыми числа

вплоть до ( pk +1 )2 являются простыми (здесь pk +1 – это k - тое простое число).

Действительно, если n < (pk +1)2 , то

n < pk +1 .

18

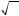
Если n осталось незачёрктутым, то оно не делится на простые числа 2, 3, 5,..., pk , в частности оно не делится на

простые числа меньшие или равные n .

ТЕОРЕМА (основная теорема арифметики). Всякое натуральное число n > 1 может быть разложено в произведение простых сомножителей. Это разложение единственно с точностью до порядка сомножителей.

ДОКАЗАТЕЛЬСТВО будет проведено индукцией по n .

СУЩЕСТВОВАНИЕ. Если n = 2 , то n очевидно представимо в виде произведения одного простого сомножителя 2.

Пусть для всех чисел, меньших некоторого n , существование разложения доказано. Докажем существование разложения для n .

Если n – простое, то как уже отмечалось n представимо в виде произведения одного простого сомножителя, равного n . Если n – составное, то

n = n1n2, 1 < n1 < n, 1 < n2 < n .

По предположению индукции числа n1, n2 раскладываются в произведение простых сомножителей:

n1 = p1p2 ×K× pk , n2 = q1q2 ×K× qs .

И в результате

n = p1p2 ×K× pkq1q2 ×K× qs .

ЕДИНСТВЕННОСТЬ. Если n = 2 , то единственность разложения очевидна.

Пусть для всех чисел, меньших некоторого n , единственность разложения доказана. Докажем единственность для n .

Пусть есть два разложения числа n в произведение простых сомножителей:

19

n = p1p2 ×K× pk , n = q1q2 ×K× qs .

Так как произведение p1p2 ×K× pk делится на простое число q1 , то по следствию из свойства 1 один из сомножителей (пусть для простоты обозначений это будет p1 ) делится на q1 . В силу простоты чисел p1 и q1 имеем p1 = q1. Сокращая равенство на p1 = q1, получаем

p2 ×K× pk = q2 ×K× qs = n1 < n .

По индукционному предположению полученные два

n = p1p2 ×K× pk = q1q2 ×K× qs

также отличаются только порядком сомножителей.

Теорема доказана.

В разложении числа в произведение простых сомножителей простые сомножители могут повторяться. Объединив их в степень, получим

СЛЕДСТВИЕ (каноническое разложение). Всякое натуральное число n > 1 может быть разложено в произведение степеней простых сомножителей:

n = pα1 pα2 ×K× pαk ,

1 2 k

где p1, p2,K, pk – попарно различные простые числа.

Это разложение единственно с точностью до порядка сомножителей.

ПРИМЕР. Разложить на простые сомножители число

71981.

20