
statist
.pdf
Серийный отбор – это такой отбор, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий обследованию подвергаются все единицы, т. е. применяется сплошное наблюдение.
Поскольку внутри серий обследуются все без исключения единицы,
средняя |
ошибка выборки при отборе равновеликих серий |
зависит |
|||
величины |
2 |
или d |
2 |
). Серийный |
отбор |
только межгрупповой дисперсии (d~ |
w |
||||
|
х |
|
|
|
|
бывает повторным и бесповторным.
При серийном отборе используются следующие формулы.
Средняя ошибка выборки для средней
При повторном отборе:
|
2 |
|
|
d~ |
|
m~ = |
x |
. |
|
||
x |
r |
|
|
||
При бесповторном отборе:
m~х = |
d |
2 |
¸ r ´ (1 - r ¸ R). |
х~ |
Средняя ошибка выборки для доли
При повторном отборе:
|
d 2 |
|
mw = |
w |
. |
|
||
|
r |
|
При бесповторном отборе:
mw = 
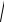 dw2 ¸ r ´ (1 - r ¸ R).
dw2 ¸ r ´ (1 - r ¸ R).
Численность выборки при определении среднего размера признака
При повторном отборе:
r= t 2 ´d 2 ¸ D2 .
~~
x x
При бесповторном отборе:
r = t |
2 |
2 |
2 |
2 |
2 |
). |
|
´d~ |
´ R ¸ (R ´ D~ + t |
|
´d~ |
||
|
|
x |
x |
|
x |
|
Численность выборки при определении доли признака
При повторном отборе:
61

r = t 2 ´dw2 ¸ D2w .
При бесповторном отборе:
r = t 2 ´dw2 ´ R ¸ (R ´ D2w + t 2 ´dw2 ),
где R – общее число серий;
r – число отобранных серий.
Межгрупповая дисперсия (dw2 ) определяется по формуле:
2 |
~ |
~ |
2 |
¸ r , |
d w |
= å(xi |
- x ) |
|
где ~ – средняя i-й серии;
xi
~ – средняя по всей выборочной совокупности.
x
Межгрупповая дисперсия доли (dw2 ) определяется по формуле:
d w2 = å(wi - w )2 ¸ r ,
где wi – доля признака i-й серии;
w – общая доля признака во всей выборочной совокупности.
7.5 Способы распространения выборочных данных на генеральную совокупность
Конечная цел любого выборочного наблюдения– распространение его характеристик на генеральную совокупность. Существуют два способа распространения данных выборочного наблюдения на генеральн совокупность: прямого пересчета и поправочных коэффициентов.
Способ прямого пересчетаприменяется в том случае, если цель выборочного наблюдения заключается в определении объема признака генеральной совокупности, когда известна лишь численность ее единиц.
Способ поправочных коэффициентовприменяется в тех случаях,
когда цель выборочного метода состоит в уточнении результатов сплошного наблюдения.
62

|
7.6 Малые выборки и их особенности |
|
||
Малая |
выборка – |
несплошное |
статистическое |
обследование, |
численность единиц которого не превышает 30. |
|
|
||
Для определенного |
способа отбора |
единиц величина стандартной |
||
ошибки зависит от объема выборки и степени колеблемости изучаемого признака в генеральной совокупности. Причем, чем меньше объем выборки, тем большую величину стандартной ошибки следует ожидать, а это снижает точность оценки параметров генеральной совокупности.
Для оценки возможных пределов ошибки малой выборки применяется отношение Стьюдента (t), определяемое по формуле:
= (~ - )¸ m , t x x м.в.
где mм.в. – величина среднего квадратического отклонения малой выборки.
mм.в. = |
s 2 |
|
= |
|
s |
|
. |
(n -1) |
|
|
|
||||
|
|||||||
|
|
|
n -1 |
||||
Величина s вычисляется на основе данных выборочного наблюдения. Она равна:
|
(хi |
- |
~ |
2 |
|
s = |
х ) |
. |
|||
|
n |
|
|||
|
|
|
|
|
|
Таким образом, теоретическое распределение отношения Стьюдента (t) имеет дело с величинами, определяемыми непосредственно по данным выборки. Для отдельных значенийt и n доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента, которые приводятся в учебниках по математической статистике.
Предельная ошибка малой выборки рассчитывается по формуле:
D м.в. = t ´ mм.в. .
Порядок расчетов тот же, что и при больших выборках.
63
8.КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ
8.1Изучение причинно-следственных отношений в статистике
Причинно-следственными |
отношениями называют |
такие связи |
между явлениями и процессами, |
когда изменение одной из |
них(причины) |
ведет к изменению другого (следствия).
Статистика не занимается выяснением этих причин, этим занимаются специальные экономические дисциплины. Статистика выявляет наличие и направление связи, количественно оценивает воздействие каждой причины на вариацию конкретного признака, выражает связь аналитически, что позволяет учитывать указанное воздействие при принятии управленческих
решений различного уровня. |
|
В процессе исследования зависимостей вскрываются |
причинно- |
следственные отношения, что позволяет выявить факторы(причины), |
|
оказывающие существенное влияние на вариацию изучаемых явлений и
процессов. |
|
|
|
|
|
|
Причина |
— это |
совокупность |
условий, обстоятельств, действие |
|||
которых приводит к появлению следствия. |
|
|
||||
Таким |
образом, |
на |
основе |
проведения |
качественного |
анализа |
появляется возможность разделить признаки на два класса: |
|
|||||
1)факторные признаки (факторы), которые обусловливают изменение других признаков;
2)результативные признаки, которые изменяются под действием факторных признаков.
Виды связей. Связи между явлениями классифицируют по различным
направлениям: |
характеру, степени тесноты, направлению, |
аналитическому |
|
выражению и т.д. |
|
|
|
По |
характеру зависимости |
различают |
функциональную |
стохастическую связь. Связь между |
признаками называютфункциональной |
||
(детерминированной), если каждому значению одного из них ответствует одно (или несколько, в случае множественных связей) вполне определенное значение другого. Такая зависимость является строгой, точной, полной.
Схематично функциональную связь можно представить следующим образом: X => Y.
В общем виде функциональную связь можно записать: yi = f(xi)
Такой вид связи достаточно часто проявляется в математике, физике, химии. Характерной особенностью функциональных связей является то, что
для таких связей всегда известен: |
|
|
|
||
– |
полный |
перечень |
фактор, |
овпределяющих |
величину |
результативного признака; |
|
|
|
||
– |
механизм |
влияния, выраженный |
определенным |
уравнением |
|
(функцией). |
|
|
|
|
|
64
Для социально-экономических явлений характерно ,точто наряду с существенными факторами, определяющими в основном величину результативного признака, на него оказывают воздействие многие другие, в том числе и случайные факторы. Поэтому существующая зависимость не проявляется здесь в каждом отдельном случае, как при функциональных связях, а лишь в общем при большом числе наблюдений. Такая зависимость называется стохастической.
Зарождение стохастической теории статистики в России относитсяк 1880 г. Термин «стохастическая теория статистики» (от греч. stochastikos — предполагать) принадлежит Я. Бернулли. В научный оборот этот термин был введен В.И. Борткевичем, который указывал на то, что в реальной жизни мы
сталкиваемся с событиями, каждое из которых является следствием нескольких причин.
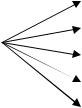
При стохастической зависимости изменение факторного признака приводит к изменению закона распределения результативного признака(рис.
8.1).
Y1
Y2
X
Y3
…
Yn
Рис. 8.1 – Схема стохастической связи
Особенностью стохастических связей является , точто для них не |
|
|||||||
известен: |
|
|
|
|
|
|
|
|
– |
полный |
|
перечень |
фактор, |
овпределяющих |
величину |
|
|
результативного признака; |
|
|
|
|
|
|||
– |
механизм |
влияния, выраженный |
определенным |
уравнением, |
|
|||
функцией. |
|
|
|
|
|
|
|
|
Частным случаем стохастической связи являетсякорреляционная, при |
|
|||||||
которой |
изменение |
среднего |
значения |
результативного |
при |
|||
обусловлено изменением факторного признака. |
|
|
|
|
||||
Корреляционная связь является неполной, нестрогой и проявляется |
|
|||||||
лишь |
при достаточно |
большом |
числе |
случаев. Схематично |
ее можно |
|
||
представить следующим образом: X => Y̅.
В общем виде корреляционную связь можно записать: ̅у̅i = f(xi). Корреляционная связь не существует без стохастической и служит
важнейшей характеристикой последней. |
|
|
|
||
Соотношение между ними аналогично соотношениюмежду средней и |
|
||||
рядом |
распределения. Ряд |
распределения |
дает |
наиболее |
полну |
65
характеристику |
|
совокупности. Средняя |
же |
|
не |
|
существует |
без |
ряд |
|||||||
распределения и в то же время служит его важнейшей характеристикой. |
|
|
||||||||||||||
|
Стохастическая |
связь |
дает |
наиболее |
|
полную |
|
характерис |
||||||||
взаимосвязи признаков. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
По степени тесноты связи делятся на слабые, умеренные и сильные |
|
||||||||||||||
(тесные). Количественные критерии оценки тесноты связи дает статистика. |
|
|||||||||||||||
|
По |
направлению различают |
связи |
прямые |
и |
обратные. При прямой |
|
|||||||||
связи |
с |
|
увеличением(уменьшением) |
значений |
|
факторного |
признака |
|
||||||||
происходит увеличение (уменьшение) |
значений |
|
результативного. |
При |
|
|||||||||||
обратной |
связи |
с ростом(снижением) |
факторного |
признака |
значения |
|
||||||||||
результативного уменьшаются (увеличиваются). |
|
|
|
|
|
|
|
|
||||||||
|
По |
аналитическому выражениювыделяют |
связи |
прямолинейные |
|
|||||||||||
(линейные) |
и |
|
криволинейные (нелинейные). |
Линейной |
является |
|
||||||||||
статистическая связь, которая приближенно выражена уравнением прямой. |
|
|||||||||||||||
Если связь выражается уравнением какой-либо кривой линии(параболы, |
|
|||||||||||||||
гиперболы показательной и т.д.), то она является нелинейной. |
|
|
|
|||||||||||||
|
В зависимости от количества факторов, влияющих на результат, |
|
||||||||||||||
различают парную и многофакторную (множественную) связь. Парная |
|
|||||||||||||||
корреляция |
– |
частный |
случай |
отражения |
связи |
некоторой |
зависимой |
|||||||||
переменной, |
с |
|
одной стороны, и одной |
из |
|
множества |
независимых |
|||||||||
переменных |
– |
с |
другой. |
Следовательно, |
парная |
связь – |
это связь |
двух |
|
|||||||
признаков. Когда же требуется охарактеризовать связь всего множества независимых переменных с результативным признаком, то применяют множественную корреляцию. Следовательно, если несколько факторов влияет на результативный признак, то связь будет многофакторной.
Существуют также связи непосредственные, косвенные и ложные. В
первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками.
Источники ложной корреляции выявил К. Пирсон. Ложная связь – это связь, установленная между признаками, не имеющими причинной связи друг с другом, являющейся следствием воздействия, общей причины. Это связь, выявленная формально , икак правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы
или же бессмысленна. |
|
|
|
|
|
Основные |
методы |
изучения |
связей. К |
методам |
изучения |
корреляционных |
связей |
относятся: графический, |
аналитических |
||
группировок, параллельных рядов, а также дисперсионный, корреляционный и регрессионный анализ и др.
Метод параллельных рядовоснован на сопоставлении двух или нескольких рядов статистических величин. Простое сопоставление значений
66
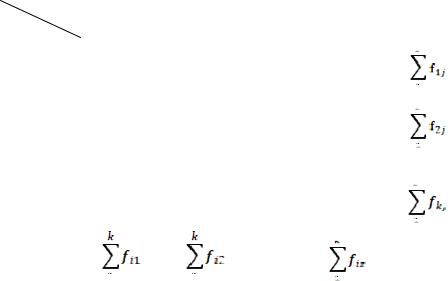
показателей |
дает |
возможность |
установить |
наличие |
|
связи |
и |
получи |
||||||||||||||||
представление о ее характере. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Метод аналитических группировокпозволяет установить |
наличие |
||||||||||||||||||||||
или |
|
отсутствие |
влияния |
двух |
или |
более |
|
факторов |
|
на |
изм |
|||||||||||||
результативного признака, а также направление связи. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Основной принцип исследования взаимосвязей с помощью метода |
|||||||||||||||||||||||
группировок заключается в том, что обычно в качестве группировочного |
||||||||||||||||||||||||
признака |
выбирают |
факторный. В |
|
сказуемом |
|
таблицы |
|
размещают |
||||||||||||||||
абсолютные, |
относительные |
или |
средние |
|
значения |
|
результативног |
|||||||||||||||||
показателя. Далее изучается, как изменение факторного признака приводит к |
||||||||||||||||||||||||
изменению результативного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Простейшим |
приемом |
выявления |
|
связи |
|
между |
двумя |
признаками |
|||||||||||||||
является построение корреляционной таблицы. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
Y |
|
|
Y1 |
|
|
Y2 |
|
… |
|
Yz |
|
|
Итого: |
|
|
Yi̅ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
|
|
f11 |
|
|
f12 |
|
… |
|
f1z |
|
|
|
|
|
|
|
Y1̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X2 |
|
|
f21 |
|
|
f22 |
|
… |
|
f2z |
|
|
|
|
|
|
|
Y2̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
… |
|
|
… |
|
… |
|
… |
|
|
… |
|
|
|
… |
|
|
|
|
|
|
|
Xk |
|
|
fk1 |
|
|
fk2 |
|
… |
|
fkz |
|
|
|
|
|
|
|
Yk̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Итого: |
|
|
|
|
|
|
|
… |
|
|
|
|
n |
|
|
|
Y̅ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Среднее |
|
|
X1̅ |
|
|
X2̅ |
|
… |
|
Xz̅ |
|
|
X̅ |
|
|
|
– |
|
|
|
||
|
В основу группировки положены два |
|
изучаемых |
во |
взаимосвязи |
|||||||||||||||||||
признака – X |
и Y. Частоты f i j показывают количество |
соответствующих |
||||||||||||||||||||||
сочетаний X и Y. Если fi j |
расположены в таблице беспорядочно, то можно |
|||||||||||||||||||||||
говорить об отсутствии связи между переменными. |
|
|
|
|
|
|
|
|
сочетанияf y |
|||||||||||||||
|
В |
случае |
образования |
какого-либо |
|
характерного |
|
|||||||||||||||||
допустимо утверждать о связи междуX и |
Y. |
При |
этом |
|
еслиf i j |
|
||||||||||||||||||
концентрируется около одной из двух диагоналей, то имеет место прямая или |
|
|||||||||||||||||||||||
обратная линейная связь. В итогах корреляционной таблицы по строкам и |
||||||||||||||||||||||||
столбцам |
приводятся |
два |
распределения– одно по X , |
другое по Y. Метод |
|
|||||||||||||||||||
группировки позволяет не только определить тесноту связи, но и измерить ее |
|
|||||||||||||||||||||||
тесноту на основе использования показателей вариации. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
Графический |
метод позволяет изобразить |
взаимосвязь |
между при- |
||||||||||||||||||||
знаками с помощью корреляционного поля(«поля рассеяния»), которое |
|
|||||||||||||||||||||||
является |
наглядным |
изображением |
корреляционной |
таблицы. В |
системе |
|||||||||||||||||||
67

координат на оси абсцисс откладываются значения факторного признака, |
|
|||
на оси ординат – результативного. |
|
|
|
|
По расположению точек, их |
концентрации |
в определенном - |
на |
|
правлении можно судить о наличии связи. |
|
|
||
8.2 Корреляционно-регрессионный анализ |
|
|||
Из всех перечисленных методов корреляционно-регрессионный анализ |
|
|||
является наиболее совершенным, так как он позволяет не только выявить, но |
|
|||
и выразить имеющуюся связь в |
виде определенного математическог |
|||
уравнения, которое |
характеризует |
механизм |
взаимодействия |
межд |
факторами и результативными признаками. Корреляционно-регрессионный |
|
||||
анализ включает в |
себя измерение тесноты связи, направления связи и |
|
|||
установление аналитического выражения(формы) связи. Теоретически он |
|
||||
разделяется на два вида анализа: корреляционный и регрессионный. |
|
|
|||
Обязательными |
условиями |
применения |
корреляционного |
и- |
рег |
рессионного анализа являются:
1)случайный отбор обследуемых единиц;
2)однородность совокупности по изучаемому признаку;
3)достаточно большое число обследуемых единиц;
4)все факторные признаки должны иметь количественное выражение.
Статистические методы изучения корреляционных зависимостей
Корреляционный анализ
-предварительная оценка связей
-количественная оценка тесноты связей
-оценка существенности связей
Регрессионный анализ
-построение уравнения регрессии
-экономическая интерпретация параметров уравнения регрессии
-применение уравнения регрессии
Выявления |
|
Прогнозирование |
резервов |
|
результатов |
|
|
|
68
8.2.1. Корреляционная связь и ее статистическое изучение
Корреляция |
– это статистическая |
зависимость между |
случайными |
величинами, не |
имеющими строгого |
функционального |
характера, при |
которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Различают три вида корреляции:
1)парная – связь между двумя признаками(результативным и факторным или двумя факторными);
2)частная – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;
3)множественная – зависимость результативного признака от двух и более факторных признаков.
Основные задачи корреляционного анализа сводятся к следующим:
1)количественно |
охарактеризовать |
тесноту |
связи |
||
результативным и факторными признаками; |
|
|
|||
2)выявить |
направление |
изменения |
результативного |
признака |
|
зависимости от роста или снижения факторного; |
|
|
|||
3)ответить на вопрос: случайна или не случайна выявленная связь?
При практическом применении корреляционный анализ включает
несколько этапов: |
|
|
|
|
|
|
|
1) |
постановка |
задачи |
и |
выбор |
факторных |
и |
результатив |
признаков; |
|
|
|
|
|
|
|
|
2)сбор статистического материала и его первичная обработка; |
|
|||||
|
3)предварительное изучение взаимосвязей; |
|
|
||||
|
4)исследование парных зависимостей; |
|
|
|
|||
|
5)исследование многофакторных связей; |
|
|
|
|||
|
6)оценка результатов исследования; |
|
|
|
|||
|
7)анализ результатов проведения корреляционного анализа. |
|
|||||
|
Рассмотрим выделенные этапы более подробно. |
|
|
||||
1) |
Постановка |
задачи |
и |
выбор факторных и |
результативных |
||
признаков – это один из самых ответственных этапов исследования. На данном этапе реализуется важное требование, которое состоит в том, чтобы качественный анализ предшествовал количественному и являлся критерием справедливости результатов. В противном случае полученн статистические характеристики будут представлять собой математические абстракции, лишенные практической ценности.
2) Сбор статистического материала и его первичная обработка.
При сборе материала для проведения исследования важно помнить методологической однородности собранных данных, т.е. чтобы данные были
рассчитаны |
по |
единой |
методологиипредварительное |
изучение |
взаимосвязей осуществляется с |
помощью простейших методов |
обработки |
||
данных: параллельных рядов, аналитической группировки, графиков и др. В
69
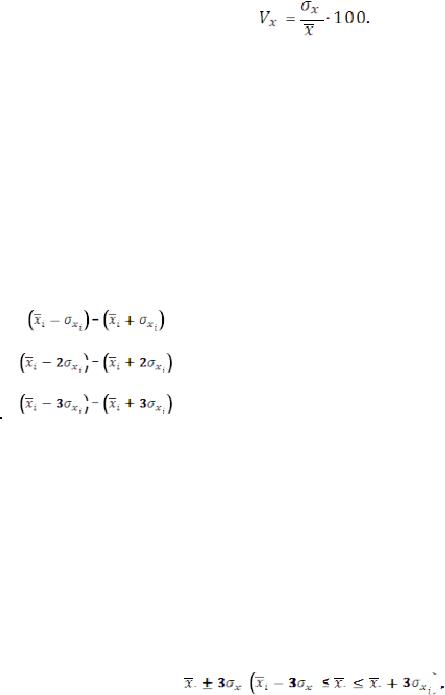
результате их применения можно дать приблизительную характеристику направления и тесноты связи. Так, в графическом методе при построении корреляционного поля можно дать первичные оценки связи.
Для оценки однородности совокупности используется коэффициент вариации по факторным признакам:
Совокупность считается однородной, если коэффициент вариации не превышает 33%. Проверка нормальности распределения исследуемых факторных признаков (x1, х2, хг, хп)проводится с помощью правила«трех сигм». Результаты проверки на нормальность распределения следует представлять в табличной форме
|
Число единиц, |
Удельный вес |
Удельный вес единиц, |
|
Интервалы значений |
единиц, входящих |
входящих в интервал, |
||
входящих в |
||||
признака-фактора |
в интервал, в |
при нормальном |
||
интервал |
||||
|
общем их числе, % |
распределении, % |
||
|
|
|||
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
68,3 |
|
|
|
|
95,4 |
|
|
|
|
99,7 |
|
|
|
|
|
Таблица 8.2.2 – Проверка нормальности распределения
Сопоставление данных гр. 3 и гр. 4 позволяет судить о наличии или об отсутствии нормальности распределения. На практике часто встречаются случаи отклонения от этих двух предпосылок. Однако это не означает, что следует отказаться от применения корреляционного анализа.
Исключение из массива первичной информации всех выделяющихся (аномальных) единиц по уровню признаков-факторов. Исключаются все единицы, у которых уровень признака-фактора не попадает в интервал и формируется новый массив для последующего анализа.
Установление |
факта |
наличия |
и |
направления |
корреляцион |
|
зависимости |
между |
результативным(у) и |
факторным (x) признаками. |
|||
Основным |
методом |
выявления наличия корреляционной связи является |
||||
метод аналитической |
группировки и определения |
групповых |
средних. Он |
|||
70
