2.3. Лінії найбільшого нахилу

Приведемо відому в нарисній геометрії теорему: прямі в площині,

перпендикулярні до її ліній рівня, є лініями найбільшого нахилу цієї

площини до площин проекцій.

Ця теорема дозволяє виконувати побудови ліній

найбільшого нахилу на КК.

Задача. Дано площину Σ(∆АВС). Побудувати її

лінії найбільшого нахилу, щодо площин проекцій

П1 і П2 (рис. 3.8), що проходять через вершину В.

Алгоритм проекційного вирішення задачі буде

наступним:

1) будують в площині Σ лінії рівня h(h1,h2) і f(f1,f2),

де h2 ║ х, f1 ║ х;

2) будують спочатку m2 ∋B2, m2 ⊥f2, потім m1;

39

3) будують спочатку n1 ∋B1, n1 ⊥h1, потім n2.

Лінія m(m1,m2) визначає найбільший нахил площини Σ до площини проекцій

П2,а лінія n(n1,n2) визначає найбільший нахил площини Σ до площини проекцій

П1 .

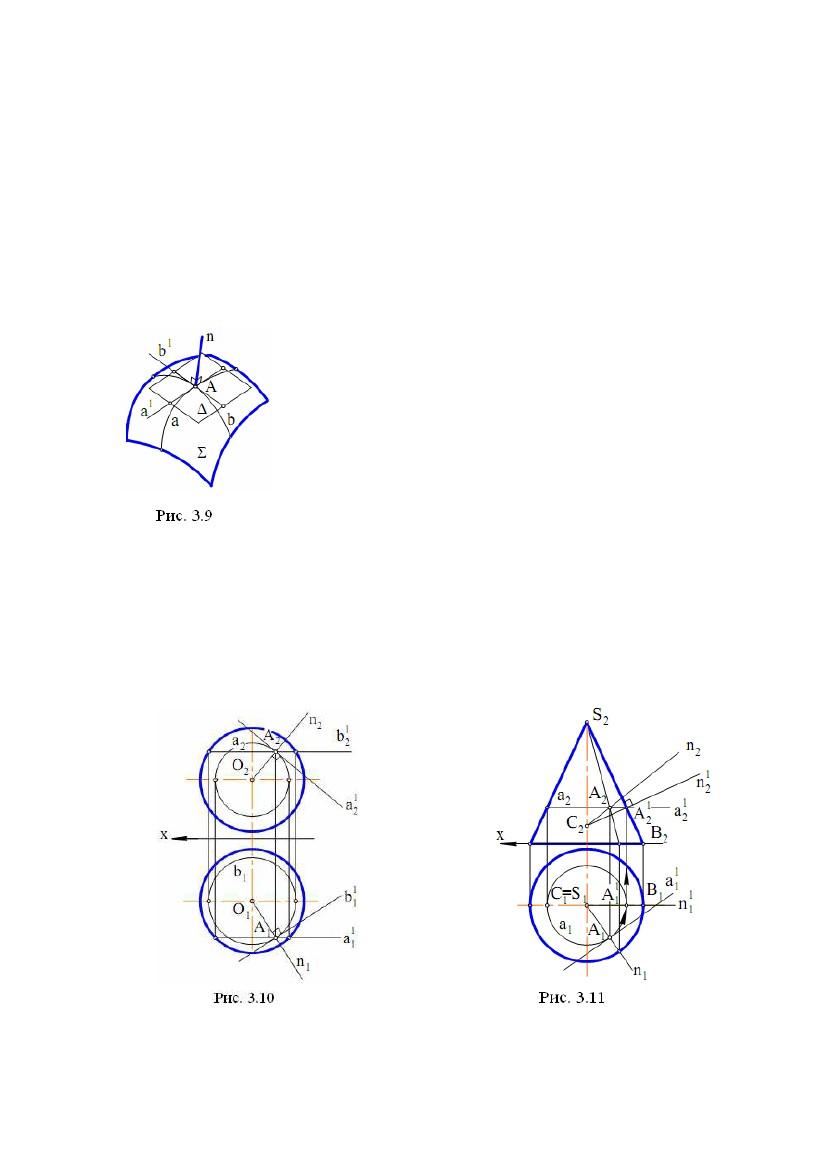
2.4. Дотична площина й нормаль до поверхні

У будь-якій точці А поверхні можна побудувати єдину дотичну

площину (рис. 3.9). Для цього на поверхні через

точку А необхідно провести дві криві a і b, а потім

побудувати дві дотичні а1 і b1відповідно к a і b.

Дотична площина ∆ утворена прямими a1 і b1.

Пряма n ⊥∆називається нормаллю поверхні у

точці А.

Задача. Дано сферу і точку А на ній. Побудувати

дотичну площину і нормаль до сфери в точці А

(рис. 3.10).

Вирішення задачі можна виконати наступним

чином:

1) побудуємо два кола а(a1, a2) і b(b1 ,b2) на сфері, що перетинаються в

точці А(А1,А2);

2) проведемо дві дотичні а1(а11, а12) і b1(b11, b12 ) до кіл a і b відповідно; шукана

дотична площина утвориться дотичними a1 і b1;

3) побудуємо нормаль n(n1,n2) до поверхні сфери по наступних умовах: n1 ⊥b11

, n2 ⊥а12. Зазначимо, що поверхня сфери складається тільки із простих точок.

Задача. Дано конічну поверхню обертання і точку А на ній. Побудувати

дотичну площину і нормаль до поверхні в точці А (рис. 3.11).

Вирішення задачі:

40

1) побудуємо на конічній поверхні дві лінії, що перетинаються в точці А:

коло а(a1, a2) і пряму b = SA(S1A1, S2A2);

2) проведемо дотичну а1(а11,а12 ) до кола а; дві пересічні в точці А прямі

a1 і SA утворять дотичну площину до поверхні конуса;

3) за допомогою перетворення обертанням (див. рис. 3.11) побудуємо

проміжне положення n1(n11,n12) шуканої нормалі n, а потім її шукане

положення n(n1,n2).

Вершина S - єдина особлива точка на поверхні конуса.

2.5. Перпендикулярність двох площин

Визначення. Дві площини називаються перпендикулярними, якщо кут

між ними дорівнює 90°. Приведемо без доказу теореми стереометрії, корисні

для вирішення наступних метричних задач:

1) Ознака перпендикулярності двох площин: якщо площина проходить

через перпендикуляр до іншої площини, то вона перпендикулярна до цієї

площини;

2) Якщо дві площини, перпендикулярні до третьої площини,

перетинаються, то пряма їхнього перетину перпендикулярна до третьої

площини;

3) Для похилої прямої, яка не є перпендикулярна до площини, має місце

твердження: через похилу проходить єдина площина, перпендикулярна до даної

площини.

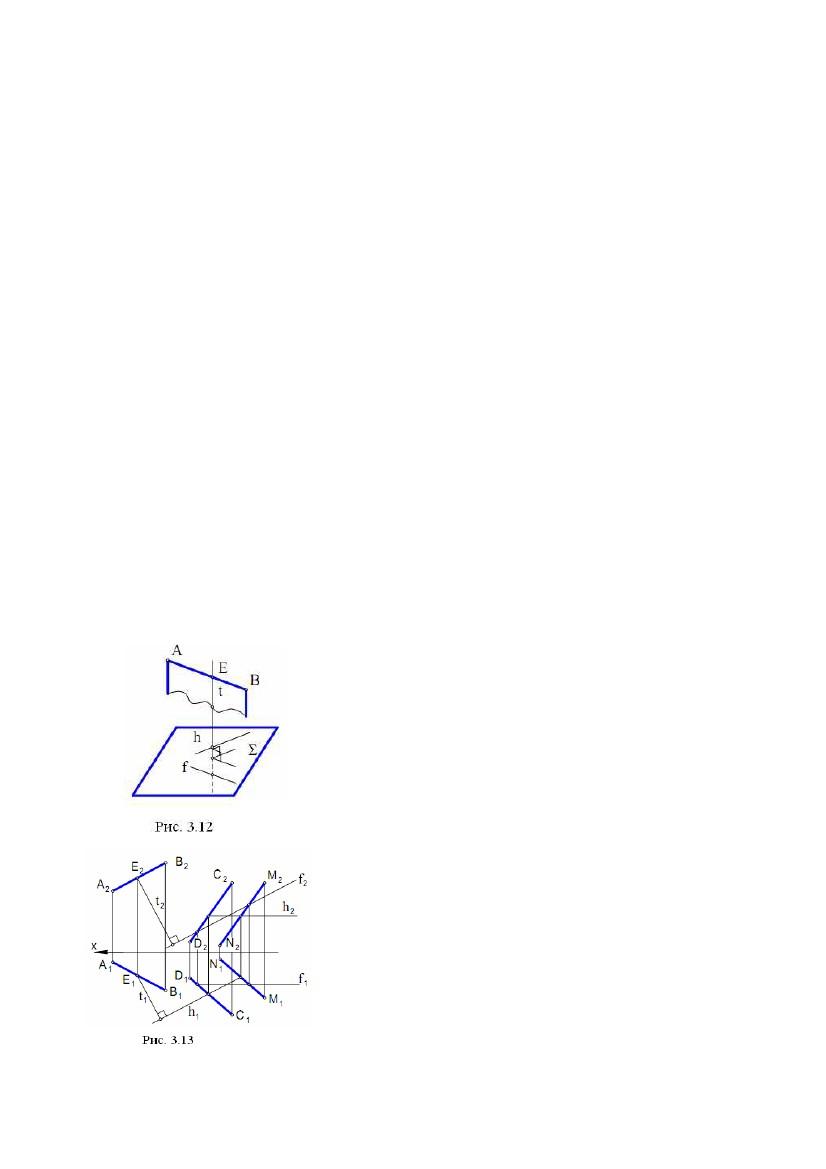
Останнє твердження дозволяє запропонувати

наступний алгоритм побудови площини, що

проходить через похилу АВ і перпендикулярну

до заданої площини :

1) на АВ вибирають довільну точку Е;

2) будують пряму t таким чином, що t ∋Е; t ⊥h ;

t ⊥f , де h ⊂, f ⊂(рис. 3.12), тобто t ⊥.

Площина (АВ, t) буде єдиною площиною,

перпендикулярною до площини . Зазначимо,

що через пряму t ⊥проходить не одна

площина, перпендикулярна до .

Задача. Дано площину (CD, MN), де

CD║MN і пряму АВ (рис. 3.13). Побудувати на

КК площину, що проходить через АВ і

перпендикулярну до площини .

Алгоритм проекційного вирішення задачі:

1) будують лінії рівня h(h1,h2) і f(f1,f2) у площині

Σ, при цьому h2║х, f1║х;

41

2) будують проекції t1 і t2 прямої t таким чином, що t2 ∋E2 , t2 ⊥f2 ; t1 ∋E1,

t1 ⊥h1 , де Е ∈АВ – довільна точка.

Площина (АВ, t) - рішення задачі.

Задача. Дано площини (АВ, DC) і ∆(KL, PT), де AB ∩DC, KL║PT, а

також точку Е. Побудувати площину, що проходить через точку Е і

перпендикулярну до обох площин і ∆(рис. 5.17).

Одне з можливих рішень даної задачі полягає в наступному. Спочатку

будують лінію перетину заданих площин t = ∩∆. Потім, на підставі

наведених теорем стереометрії, будують площину, що проходить через точку Е

і перпендикулярна до лінії t. Будучи єдиною, ця площина являє собою рішення

задачі.

Можливий інший алгоритм вирішення даної задачі (див. рис. 5.16):

1) з даної точки Е опускають перпендикуляр а на площинуΣ;

2) із точки Е опускають перпендикуляр b на площину ∆.

Площина (a, b), де a ∩b = E, є рішенням задачі. Розглянемо реалізацію

цього алгоритму на КК (див. рис. 5.17).

1) У площині Σ побудуємо лінії рівня h1(h11, h12) і f1(f11, f12). При цьому

h12║x; f11║x.

2) У площині ∆ побудуємо лінії рівня h2(h21, h22) і f 2(f21, f22). При цьому

h22║х; f21║х.

3) Із точки Е опускаємо два перпендикуляри: а ⊥Σ, b ⊥∆. При цьому

1а2 ⊥f 2 , а1 ⊥h11 ; b2 ⊥f22 , b1 ⊥h21.

Дві прямі а і b, що перетинаються в точці Е, визначають шукану

площину, тобто площину, перпендикулярну до заданих площин і ∆.

42

ЛЕКЦІЯ № 4. ПЕРЕТВОРЕННЯ КОМПЛЕКСНОГО КРЕСЛЕННЯ

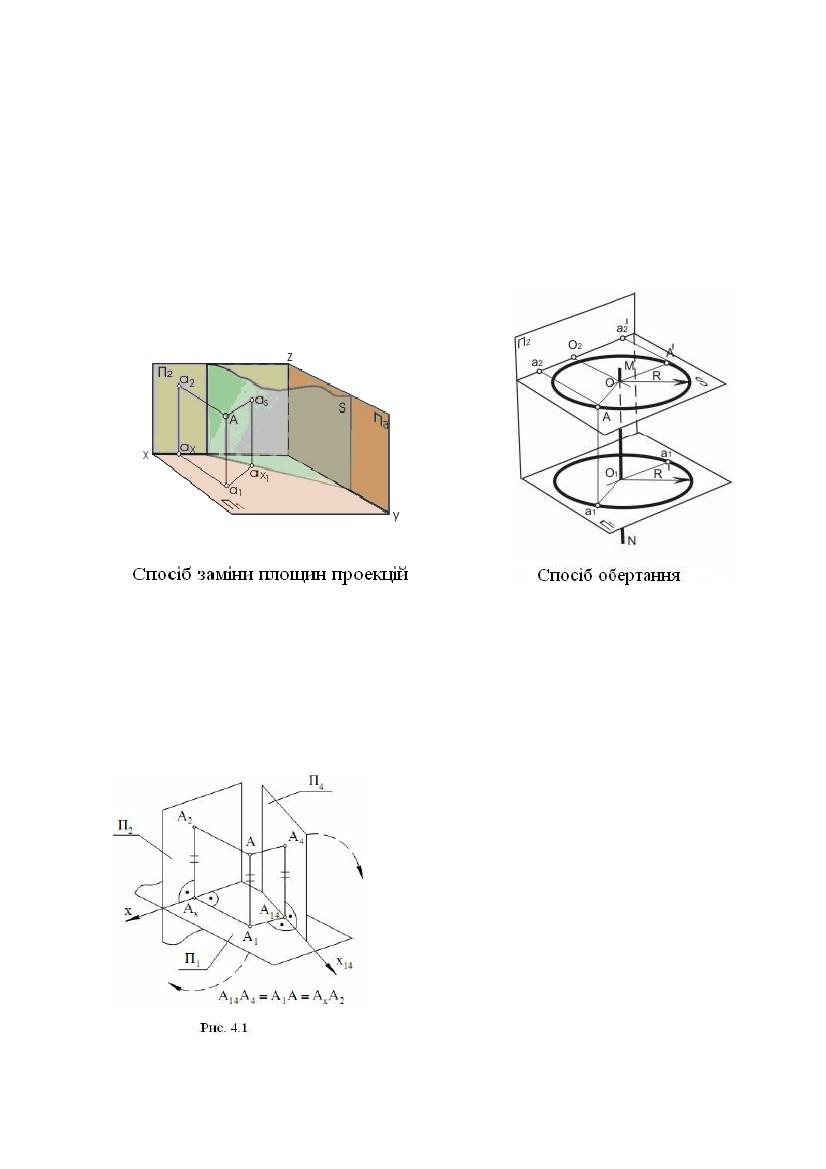
Нарисна геометрія має у своєму розпорядженні способи, за допомогою

яких можна перейти від загальних положень заданих геометричних образів до

окремих, що значно спрощує вирішення задачі й дозволяє одержати більш

точну відповідь. Ці способи називаються способами перетворення проекцій і

полягають у послідовній заміні площин проекцій і в обертанні геометричних

образів навколо певних осей.