3) Визначення кутів між фігурами.
Розглянемо приклади рішень на КЧ метричних задач у кожній групі.
2. Побудова взаємно перпендикулярних фігур
2.1 Перпендикулярність двох прямих
Визначення. Дві прямі у просторі називаються перпендикулярними,
якщо кут між ними дорівнює 90°. Перпендикулярні прямі можуть бути
пересічними або мимобіжними.
Задача. Дано пряму АВ і точку С.
Побудувати пряму, що проходить через
точку С і яка перетинає АВ під прямим
кутом (рис. 3.3).
Вирішення задачі ґрунтуєтьсяна
побудовах, що приводять до проекційного
зображення умов теореми про проекцію
прямого кута (див. рис. 3.2).
Алгоритм вирішення в символічному
записі буде наступним:
1) х1║А1В1;
2) (А2В2, А1В1) ⇒А4В4; (С2, С1) ⇒С4;
3) С4D4 ⊥А4В4;
4) D4 ⇒D1 ∈А1В1; D1 ⇒D2 ∈А2В2.
С1D1, C2D2 – рішення задачі.
37
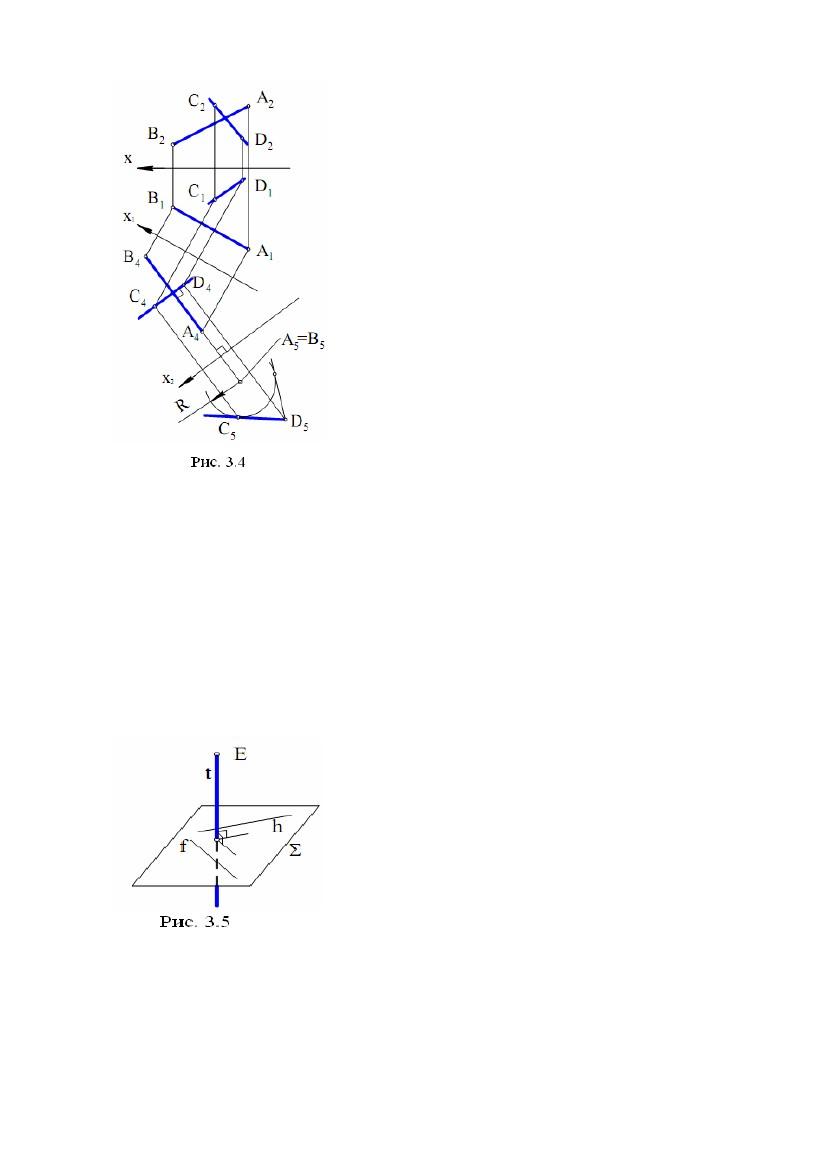Задача.
Дано пряму АВ і точку D
(рис.3.4).
Побудувати пряму, що проходить через точку
D, перпендикулярну до прямої АВ і утворюючу
з нею найкоротшу відстань R, де R < (D, AB);
- відстань між фігурами, зазначеними в
дужках.
З умови задачі випливає, що задана й шукана
пряма - мимобіжні. Кінці відрізка найкоротшої
відстані R утворять дві множини точок: пряму
АВ і циліндричну поверхню обертання з віссю
АВ. Із точки D можна провести лише дві прямі,
дотичні до циліндричної поверхні та які
утворюють кут 90° з прямою АВ. Алгоритм
вирішення даної задачі в символічному записі
має вигляд:
1) х1║А1В1;
2) (А2В2, А1В1) ⇒А4В4; (D1, D2 ) ⇒D4;
3) х2 ⊥А4В4;
4) (А1В1, А4В4 ) ⇒А5 = B5; (D1, D4 ) ⇒D5;
5) D5C5 – дотична до кола радіуса R;D4C4 ⊥А4В4;
6) (C5, C4 ) ⇒C1; (C4, C1) ⇒C2.
C2D2, С1D1 – одне з двох рішень задачі.
2.2. Перпендикулярність прямої і площини
Визначення. Пряма називається перпендикулярною до площини, якщо
вона перпендикулярна до двох пересічних прямих, що лежать у цій площині.
Приведемо без доказу відомі в
шкільному курсі стереометрії теореми,
необхідні для вирішення наступних
метричних задач.
1)Ознакаперпендикулярності
прямої і площини: якщо пряма
перпендикулярна до двох пересічних
прямих, що лежать у площині, то вона
перпендикулярна до цієї площини.
2) Через будь-яку точку простору проходить єдина пряма,
перпендикулярна до даної площини.
3)Через будь-яку точку простору проходить єдина площина,
перпендикулярна до даної прямої.
Для побудови прямої t ⊥Е, перпендикулярної до площини , необхідно,
на підставі ознаки перпендикулярності, провести в площині дві пересічні прямі
38
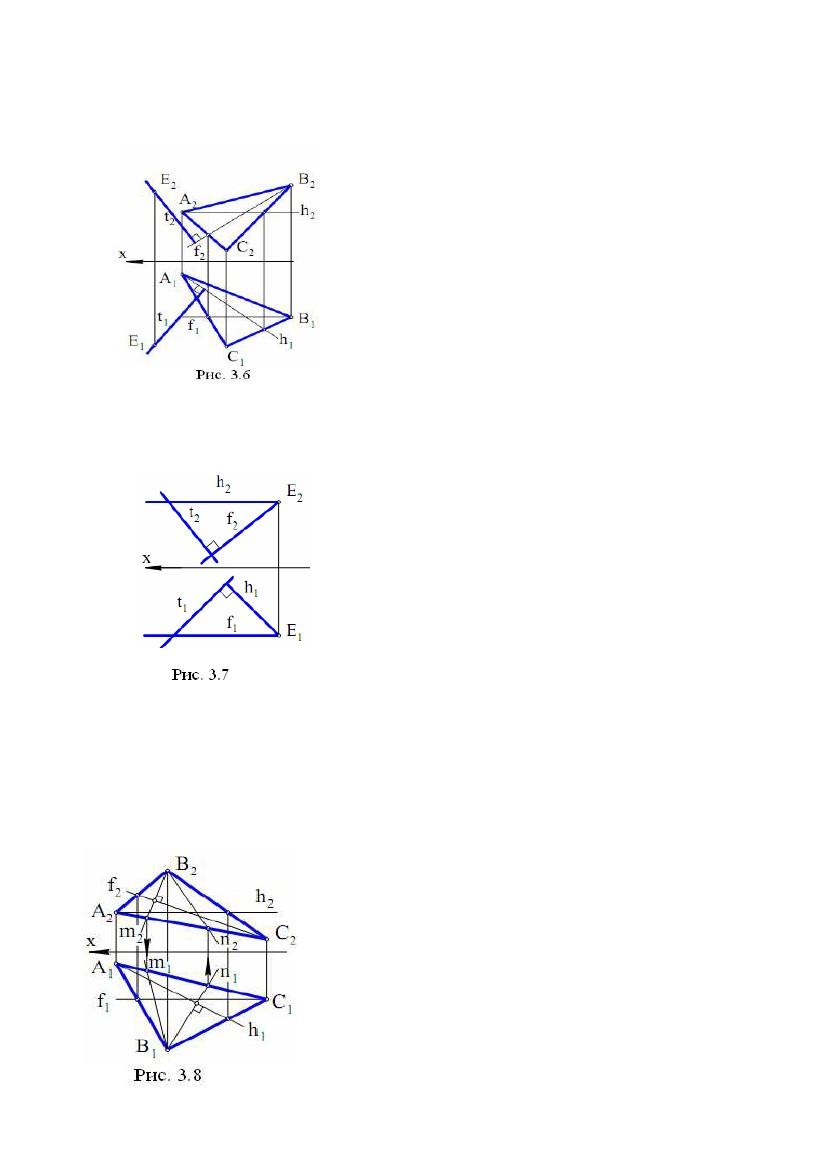h
і
f,
а
потім побудувати пряму t
за
умовами: t
⊥h,
t
⊥f
(рис.
3.5). У
загальному
випадку прямі t і h, t і f - пари мимобіжних прямих.
Задача. Дано площину (∆АВС) і точку Е.Побудувати пряму t за∆
умовами: t ∋E, t ⊥(рис. 3.6).
Вирішення задачі може бути наступним:
1) будують лінії рівня h і f у площині Σ, де
h2║х, f1║x;
2) будують проекції t1 і t2 шуканої прямої t,
де t2 ∋Е2, t2 ⊥f2; t1 ∋E1, t1 ⊥h1.
У підсумку t1 , t2 – рішення задачі. Пряма t
мимобіжна з f і h.
Вибір ліній рівня h і f у якості пересічних
прямих у площині продиктований
наведеними вище умовами теореми про
проектування прямого кута й простотою побудов на КК(комплексному
кресленні). Якщо точка Е перебуває в площині , то послідовність побудов
залишається попередньою.
Задача. Дано пряму t і точку Е. Побудувати
площину, що проходить через точку Е і
перпендикулярну до прямої t (рис. 3.7).
Вирішення задачі ґрунтується на побудові
двох ліній рівня h(h1,h2) і f(f1,f2), що проходять
через точку Е: h2 ∋E2, h2║х, h1 ∋E1, h1 ⊥t1 ; f1
∋E1, f1 ║х, f2 ∋E2, f2 ⊥t2 .
Площина (h , f ) - рішення задачі