1 Складний опір (combined stress)

Під складним опором розуміють різні комбінації простих навантажень бруса (розтягання (tension), стискання (compression), зсуву (shear), кручення (torsion) та згинання (bending).

У загальному випадку навантажування бруса у поперечних перерізах можуть діяти шість компонент внутрішніх сил – N, Q_y, Q_z, M_y, M_z, M_кр, пов’язаних з чотирма простими деформаціями стрижня – розтяганням (стисканням), зсувом , крученням та згинанням.

1.1 Позацентрове розтягання (стискання) прямого бруса

1.1.1 Короткі теоретичні відомості

Позацентрове розтягання-стискання (eccentric tension-compression) є окремим випадком складного згинання з розтяганням (стисканням), при якому брус розтягується силами, паралель­ними осі бруса, так що рівнодійна їх не збігається з віссю бруса (рис. 1.1), а проходить крізь точку р, що називається полюсом сили.

Нехай на брус довільного перерізу діє одна сила Р, яка паралельна осі бруса й пе­ретинає довільний поперечний переріз у точці р (рис. 1.1). Координати цієї точки в системі головних осей перерізу позначимо через у_р та z_р, а відстань цієї точки до осі х, яка називається ексцентри­ситетом (eccentricity), – через е. У довільному поперечному перерізі при певному на­вантаженні діють такі внутрішні силові фактори: N = Р; М_у = Рz_р; М_z = Ру_р.

Отже, напруження в довільній точці перерізу складатимуться з напру­жень осьового розтягання силою N та напружень від чистого згинання моментами М_у та М_z:

. (1.1)

Підставивши сюди замість N, М_у та М_z їхні значення, дістанемо

. (1.2)

Ця формула набере дещо іншого вигляду, якщо виразити головні мо­менти інерції через радіуси інерції:

. (1.3)

Для визначення небезпечної точки при складному профілі доцільно побудувати нейтральну лінію перерізу. Небезпечною в перерізі буде точ­ка, найвіддаленіша від нейтральної лінії.

Рівняння нейтральної лінії матимемо, прирівнявши до нуля праву частину рівняння (1.3) і позначивши координати точок на нейтральній лінії через y₀ та z₀:

. (1.4)

Поклавши в цьому рівнянні по черзі z₀ = 0 і у₀ = 0, знайдемо відрізки у_н та z_н, що відсікаються нейтраль­ною лінією на осях у та z (рис. 1.2):

; (1.5)

Із залежностей (1.5) випливає, що нейтральна лінія перетинає координатні осі в точках, які належать квадранту, протилежному тому, в якому лежить точка р.

Тепер, провівши паралельно ней­тральній лінії дотичні до контуру перерізу, знайдемо найбільш напру­жені точки А та В у розтягнутій та стиснутій зонах перерізу (рис. 1.2).

Напруження в цих точках та умови міцності мають вигляд

;

(1.6)

.

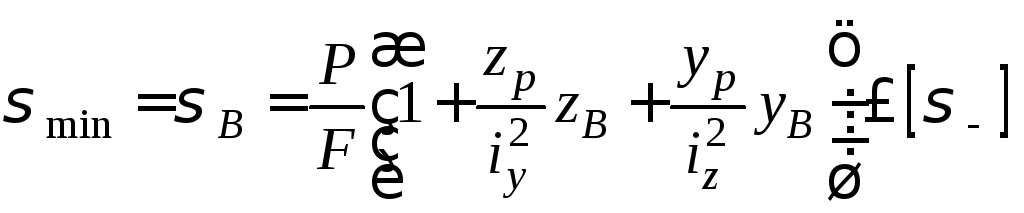Тут z_А, у_А та – z_B , – у_B –– координати точок А та В відповідно. Епю­ру напружень σ наведено на рис. 1.2. Для прямокутного перерізу умову міцності зручніше записати в такому вигляді:

. (1.7)

Формули (1.6) та (1.7) справедливі й у випадку дії стискальної сили Р, якщо немає небезпеки виникнення поздовжнього згинання.

Ядро перерізу (core of a cross-section). Досі ми зображали нейтральну лінію як таку, що проходить крізь переріз. Проте взагалі вона може проходити й поза перерізом. Дійсно, якщо сила Р прикладена в центрі ваги, то нейтральна лінія проходить у нескінченності, оскільки напруження в цьому разі розподілені рівномірно.

Із збільшенням ексцентриситету е (рис. 1.3) нейтральна лінія наближа­тиметься до перерізу і при деякому положенні сили Р (на рис. 1.3, на­приклад, при положенні А₃) вперше торкнеться контуру перерізу. При дальшому збільшенні ексцентриситету нейтральна лінія перетинає переріз, причому нормальні напруження в перерізі будуть обох знаків: по один бік від нейтральної лінії — розтягальними, по інший — стискальними.

Можна визначити зону таких віддалень сили Р від осі, при яких нормальні напруження по всьому поперечному перерізу будуть одного знака. Така зона називається ядром перерізу. Це важливо для брусів з матері­алів, що погано чинять опір розтяганню (наприклад, для цегляної клад­ки, для бетону та сірого чавуну).

Отже, ядром перерізу називають зону навколо центра ваги поперечного перерізу, яка має таку властивість: якщо позацентрово прикладене наван­таження розміщене в зоні ядра, то нормальні напруження в усіх точках поперечного перерізу мають один знак.

Для побудови ядра перерізу будемо задаватися різними положеннями нейтральної лінії, дотичними до контуру перерізу, й обчислювати коор­динати відповідних точок прикладання сили Р за такими формулами, що випливають з виразу (1.5):

; . (1.8)

Обчислені координати визначають точки, що лежать на межі ядра пе­рерізу.

Аби полегшити побудову ядра перерізу, використаємо таку властивість нейтральної лінії: при повороті нейтральної лінії навколо деякої фіксованої точки А контуру перерізу точка прикладання сили переміщується вздовж деякої прямої. Щоб обґрунтувати цю властивість, досить підставити в рівняння (1.4) координати точки А(у_ОА , z_ОА), що лежить на нейтральній лінії. Матимемо

. (1.9)

Дійсно, рівняння (1.9) при z_ОА = const є рівнянням прямої лінії віднос­но координат точок прикладання сили Р – (у_р, z_р).

Отже, для побудови ядра перерізу будь-якої фігури треба провести кілька положень нейтральної лінії, що збігаються зі сторонами перерізу, а також дотикаються до точок, які стирчать.

Побудуємо, наприклад, ядро перерізу для прямокутника АВСВ (рис. 1.4). Сумістимо спочатку нейтральну лінію зі стороною СD (положення 1 – 1). Очевидно, в цьому разі

; .

Тоді із виразів (1.8)

; .

Тут ураховано, що

; .

Отже, координати точки 1' ядра перерізу визначені.

Сумістимо тепер нейтральну лінію зі стороною АD (положення 2–2). Маємо

;.

Тоді координати точки 2' ядра

;.

Аналогічно визначаються коор­динати точок 3′ та 4', що відповіда­ють положенням 3 – 3 та 4 – 4 нейтральної лінії.

Оскільки при переході нейтраль­ної лінії з одного боку па інший вона повертається навколо кутової точ­ки перерізу, то точка прикладання сили переміщується по прямій, утво­рюючи контур ядра. Отже, ядро пе­рерізу буде ромбом з діагоналями, які дорівнюють одній третині відпо­відної сторони перерізу.