
- •Вінницький національний технічний університет
- • В.А. Огородніков, о.В. Грушко, і.Ю. Кириця, 2010 зміст
- •Задача 7. Розрахунок стержня на позацентровий стиск 12
- •Додаток а. Оформлення розрахунково-графічної роботи 123
- •Порядок та основні вимоги до виконання роботи
- •1 Складний опір (combined stress)
- •1.1 Позацентрове розтягання (стискання) прямого бруса
- •1.1.1 Короткі теоретичні відомості
- •1.1.2 Завдання до розрахунково-графічної роботи
- •1.2 Згинання з крученням (bending combined with torsion)
- •1.2.1 Короткі теоретичні відомості
- •1.2.2 Завдання до розрахунково-графічної роботи
- •1.2.3 Завдання до розрахунково-графічної роботи
- •2. Енергетичні методи визначення переміщень
- •2.1. Короткі теоретичні відомості
- •2.1.1 Узагальнені сили і переміщення
- •2.1.2 Загальна формула для визначення переміщень. Метод Мора
- •2.1.3 Обчислення інтегралів Мора способом Верещагіна
- •2.2 Завдання до розрахунково-графічної роботи
- •Розв’язування
- •3. Статично невизначувані системи (statically indeterminate system)
- •3.1 Короткі теоретичні відомості
- •3.1.1 Основні поняття та визначення
- •3.1.2 Канонічні рівняння (canonical equations) методу сил
- •3.1.3 Визначення переміщень у статично невизначуваних системах
- •3.1.4 Контроль правильності розв'язання статично невизначуваної системи
- •3.2 Завдання до розрахунково-графічної роботи
- •4 Стійкість стиснутих стрижнів (buckling)
- •4.1 Короткі теоретичні відомості
- •4.1.1 Стійка та нестійка пружна рівновага
- •4.1.2 Формула Ейлера для визначення критичної сили стиснутого стрижня
- •4.1.3 Вплив умов закріплення кінців стрижня на значення критичної сили
- •4.1.4 Поняття про втрату стійкості при напруженнях, що перевищують границю пропорційності
- •4.1.5 Розрахунки на стійкість за допомогою коефіцієнтів зменшення основного допустимого напруження
- •4.1.6 Перевірний розрахунок стиснутих стрижнів
- •4.1.7 Проектувальний розрахунок
- •4.2 Завдання до розрахунково-графічної роботи
- •5. Розрахунки при ударних навантаженнях (impact load)
- •5.1 Короткі теоретичні відомості
- •5.1.1 Розрахунок при осьовій дії ударного навантаження
- •5.2 Завдання до розрахунково-графічної роботи
- •6. Розрахунки конструкцій на витривалість
- •6.1 Короткі теоретичні відомості
- •6.1.1 Явище утоми матеріалів. Характеристики циклів
- •6.1.2 Визначення границі витривалості. Діаграма утоми
- •6.1.3 Вплив конструктивно-технологічних факторів на границю витривалості
- •6.1.4 Розрахунок на міцність при повторно-змінних навантаженнях
- •6.2 Завдання до розрахунково-графічної роботи
- •6.3 Приклад розв’язання задачі 14
- •Додаток а
- •Сортамент прокатної сталі
- •Геометричні характеристики деяких перерізів
- •Додаток д
- •Додаток е Довідникові дані до розрахунку стиснутих стержнів
- •Додаток ж Довідкові дані до визначення переміщень графічними методами
- •Додаток к Дані до розрахунку валів
- •Додаток л Співвідношення між деякими фізичними величинами в різних системах вимірювань
- •Додаток м
6.3 Приклад розв’язання задачі 14
Дано:
матеріал – сталь 40ХН;
![]()
![]()
Розв’язування
Показники статичної і циклічної міцності сталі 40ХН (див. додатки В, Г)
![]()
![]()
![]()
![]()
Знаходимо максимальну і мінімальну величини крутних моментів:
![]()
Креслимо розрахункову схему вала згідно з вихідними даними (рис. 6.1).
Будуємо епюри згинаючих моментів і визначаємо небезпечні перерізи вала.
Визначаємо опорні реакції (рис. 6.1).
![]()
![]()
![]()
Перевірка:
![]() ,
,
![]()
Визначаємо згинаючі моменти у характерних перерізах:
![]()
Будуємо
епюру
![]() (рис.
6.1). Крутні моменти по довжині вала
однакові. Тому небезпечні перерізи
визначаємо, орієнтуючись на розрахункову
схему вала і епюру згинаючих моментів
(рис. 6.2). Такими є перерізиС
і Е
,
тому що за наявності концентраторів
напружень у вигляді ступінчастої зміни
діаметрів тут діють згинальні моменти,
близькі до максимального.
(рис.
6.1). Крутні моменти по довжині вала
однакові. Тому небезпечні перерізи
визначаємо, орієнтуючись на розрахункову
схему вала і епюру згинаючих моментів
(рис. 6.2). Такими є перерізиС
і Е
,
тому що за наявності концентраторів
напружень у вигляді ступінчастої зміни
діаметрів тут діють згинальні моменти,
близькі до максимального.
Обчислення згинаючих моментів у небезпечних перерізах.
Переріз С:
![]()
Переріз Е:
![]()
7.
Визначимо
![]() .
Знаходимо
.
Знаходимо![]() і
і![]() - величини допустимої сили для кожного
перерізу. Менша з них і буде
- величини допустимої сили для кожного
перерізу. Менша з них і буде![]() .
.
Переріз С
Знаходимо
![]() – допустиму величину силиР
з умови міцності при згинанні.
– допустиму величину силиР
з умови міцності при згинанні.
![]()
Нормальне напруження в небезпечній точці перерізу при обертанні вала змінюється за симетричним циклом. Тому коефіцієнт запасу обчислимо за формулою

Амплітудне
напруження
![]()
Осьовий момент опору перерізу вала
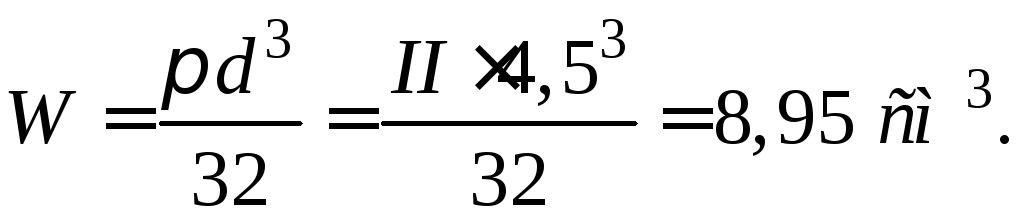 Тоді
Тоді
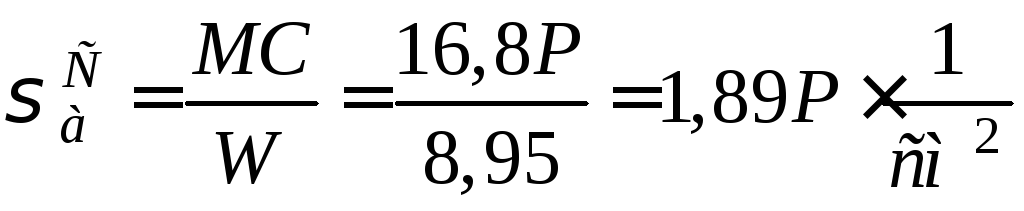 .
.
Загальний коефіцієнт зниження границі витривалості деталі при симетричному циклі знайдемо за формулою:
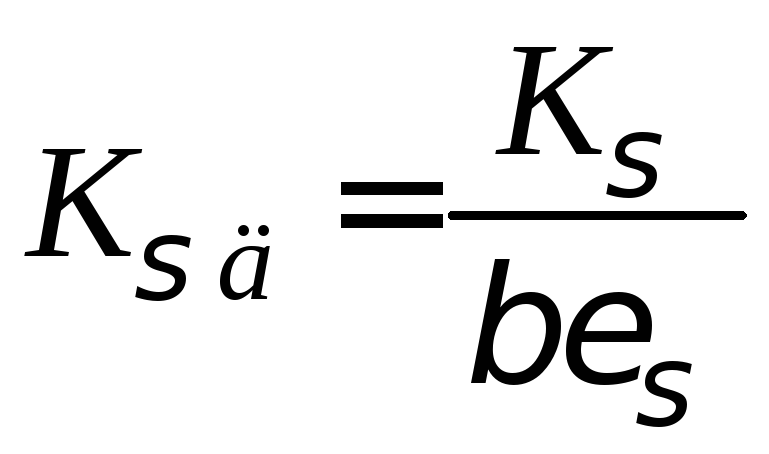 .
.
При
 і
і![]() коефіцієнти концентрації напружень
коефіцієнти концентрації напружень![]() (див. додаток Д)
(див. додаток Д)![]() (див. додаток Е). При шорсткості
(див. додаток Е). При шорсткості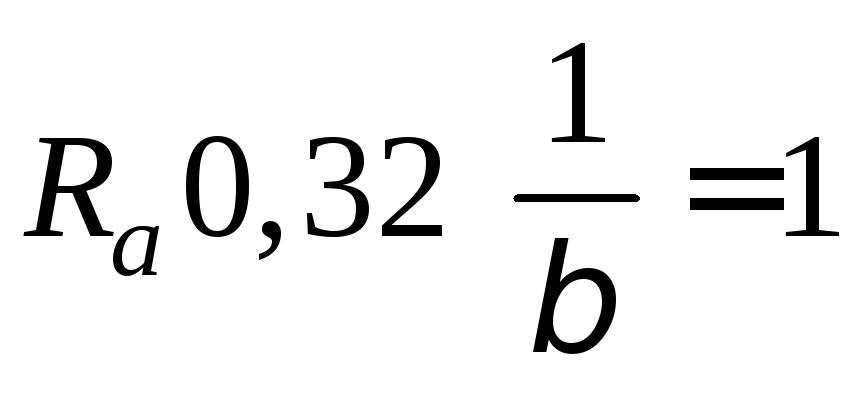 (додаток Ж)
(додаток Ж)
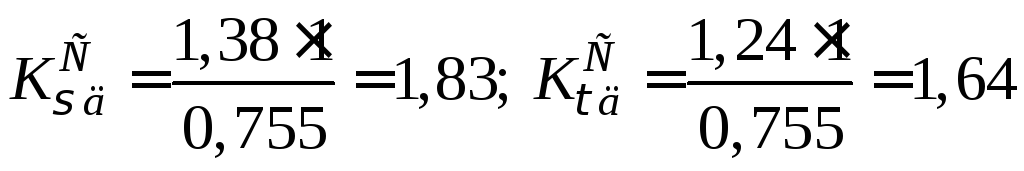
із (6.1) і (6.2) одержимо:
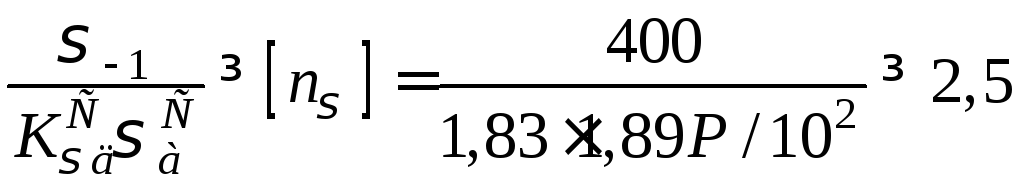

Розмірність:
![]() –
–![]() ,
,![]() .
.
ІІ
Знаходимо
![]() – допустиму величину силиР
з умови міцності при крученні
– допустиму величину силиР
з умови міцності при крученні
![]()
Матеріал
у небезпечній точці сприймає асиметричний
цикл дотичних напружень. Тому визначимо
допустиме значення сили
![]() з умови втомної міцності і сили
з умови втомної міцності і сили![]() Записуємо умову втомної міцності
Записуємо умову втомної міцності![]() .
Визначаємо коефіцієнт запасу
.
Визначаємо коефіцієнт запасу![]() по відношенню до границі витривалості.
Для цього обчислюємо добуток
по відношенню до границі витривалості.
Для цього обчислюємо добуток![]() Характеристика
Характеристика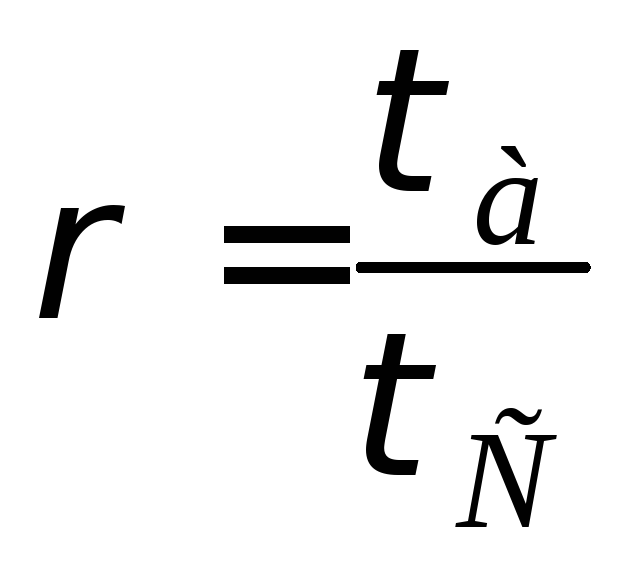 :
:

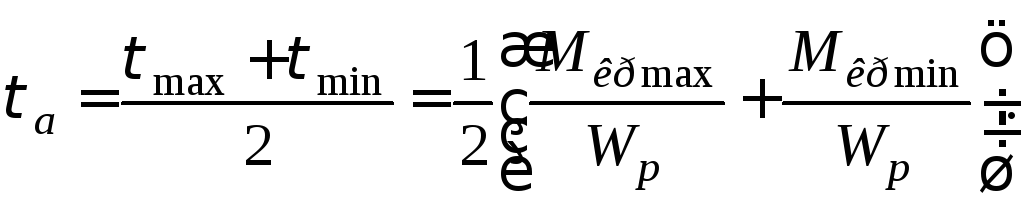
Полярний момент опору перерізу вала:

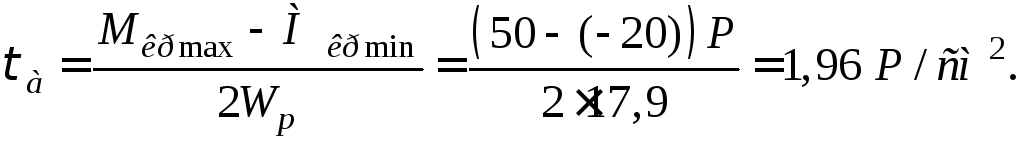
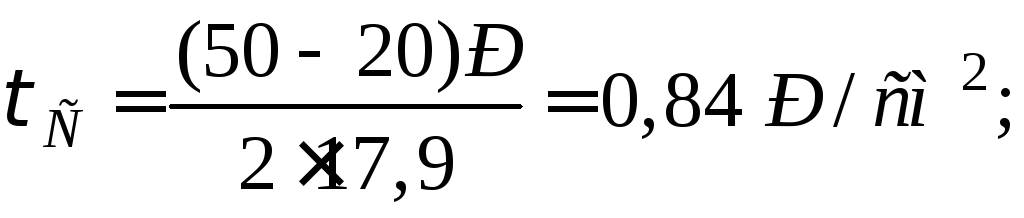

так
як величина добутку
![]() то для обчислення коефіцієнта запасу
використовуємо формулу
то для обчислення коефіцієнта запасу
використовуємо формулу
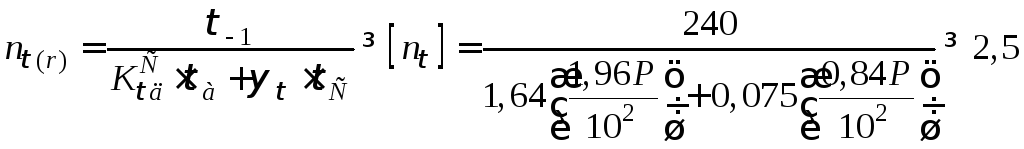

Розмірність:
![]()

Рис. 6.7. Розрахункова схема вала
Знаходження
![]()
![]() .
.
Записуємо умову статичної міцності
![]() .
.
Коефіцієнт запасу по відношенню до границі текучості обчислюємо за формулою
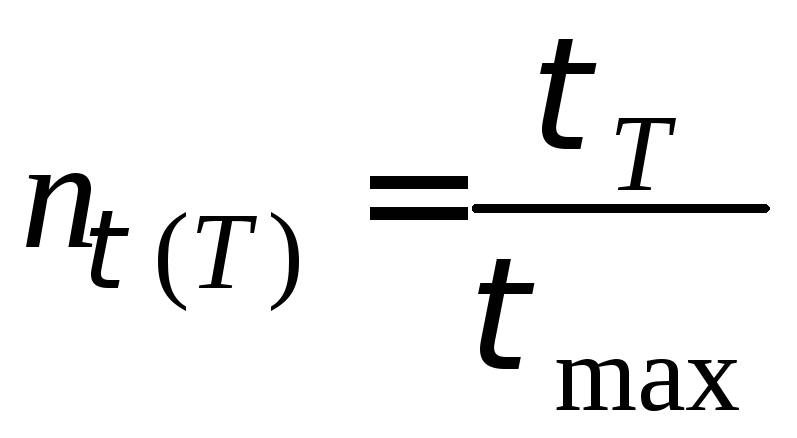 ,
,
де
![]() (6.15)
(6.15)
Враховуючи (6.13 - 6.15), одержимо
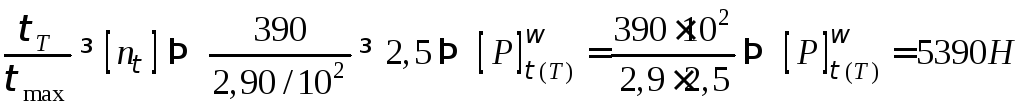 .
.
З порівняння величин
![]()
![]()
![]() .
.
Робимо
висновок, що для перерізу L
допустима величина сили
![]() .
.
Переріз Е
1.
Знаходимо![]()
 .
.
Визначаємо
коефіцієнти![]() і
і![]() .
.
При
![]() ,
,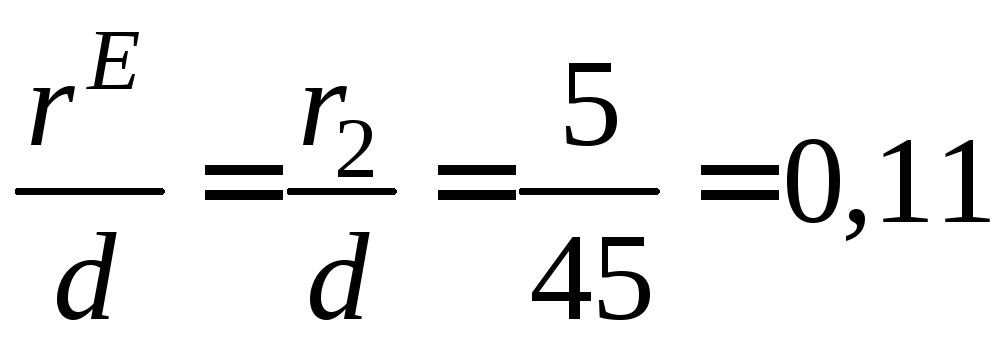 і
і![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ;
1/β=1.
;
1/β=1.
Тоді
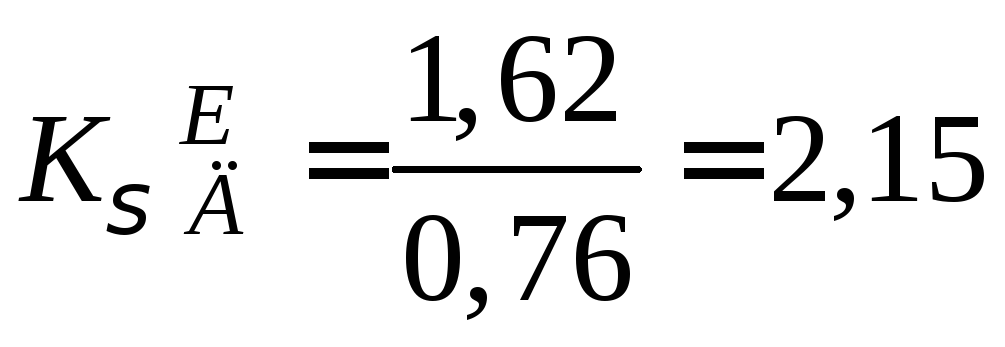 ;
;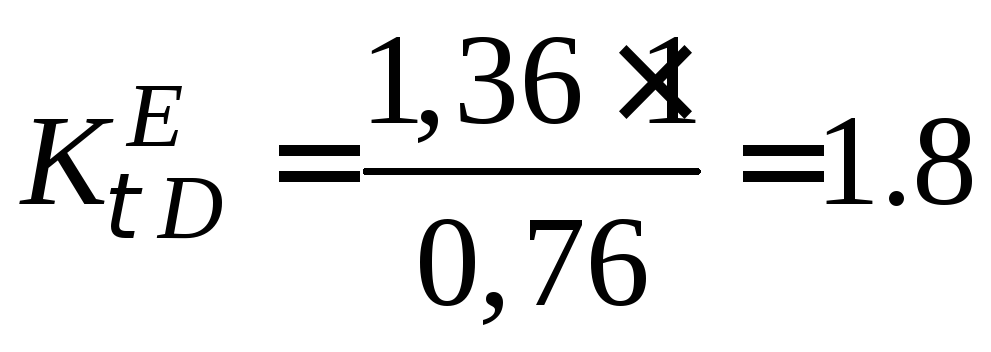
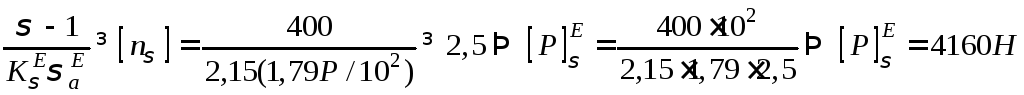 .
.
Розмірність
![]() ,
,![]() .
.
Обчислюємо
![]() при асиметричному крученні.
при асиметричному крученні.
Критерій
![]() ,
і коефіцієнт запасу по відношенню до
границі витривалості обчислюємо за
формулою
,
і коефіцієнт запасу по відношенню до
границі витривалості обчислюємо за
формулою
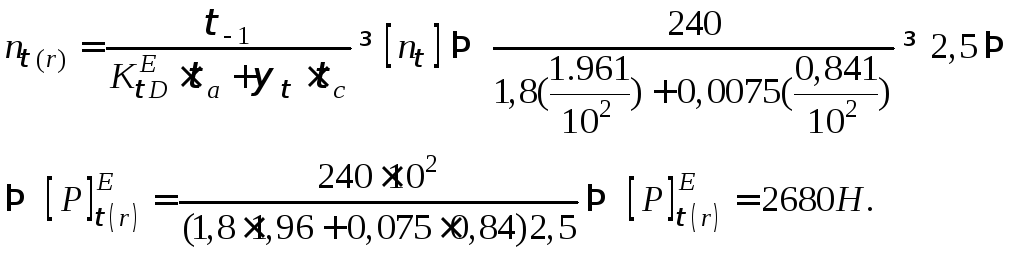
Амплітудні
![]() і середні
і середні![]() напруження в перерізахL
і E
однакові. Тому
напруження в перерізахL
і E
однакові. Тому
![]() .
.
Як
видно з порівняння
![]() ,
,![]() і
і![]() ,
для перерізу Е допустима величина сили
,
для перерізу Е допустима величина сили![]() .
.
Отже, допустима величина сили Р для вала визначається втомою міцністю матеріалу в небезпечній точці перерізу Е.
![]() .
.
Обчислення коефіцієнта запасу міцності
При плоскому напруженому стані коефіцієнт запасу визначають за формулою
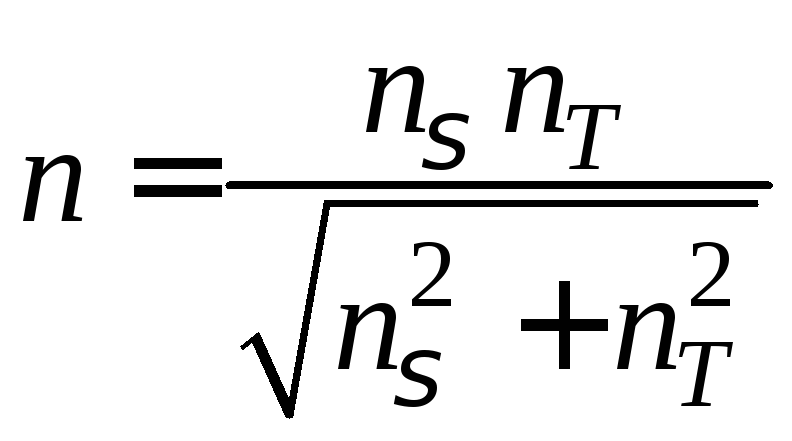 .
.
Обчислюємо n для кожного ймовірно небезпечного перерізу. Менша величина є коефіцієнтом запасу вала.
Коефіцієнт
запасу
![]() по нормальному напруженню обчислюється
в небезпечній точці перерізівL
і E
.
по нормальному напруженню обчислюється
в небезпечній точці перерізівL
і E
.
Переріз L
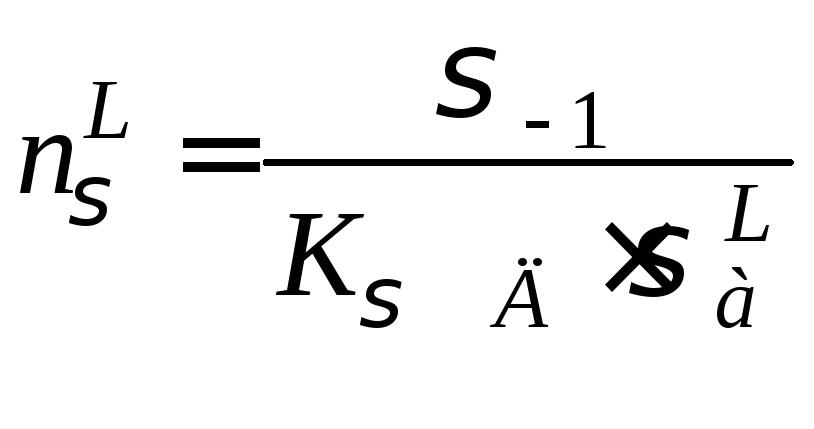 ,
,
![]() МПа.
МПа.
Тоді
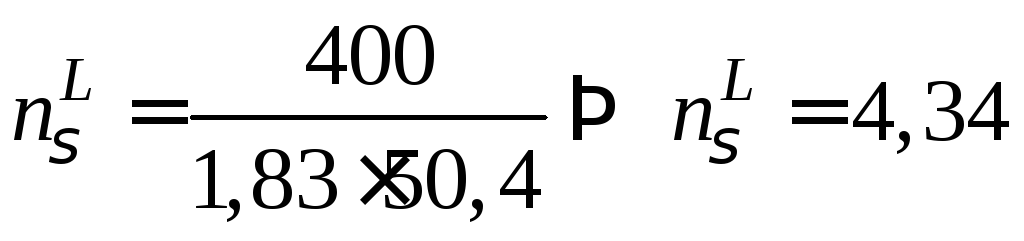 ,
,
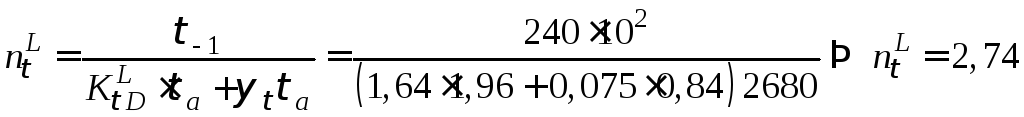 ,
,
![]()
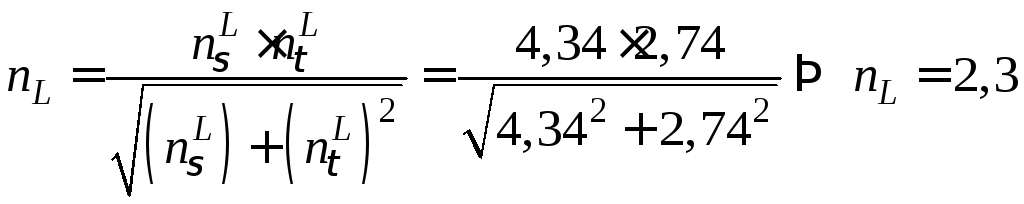 .
.
Переріз Е
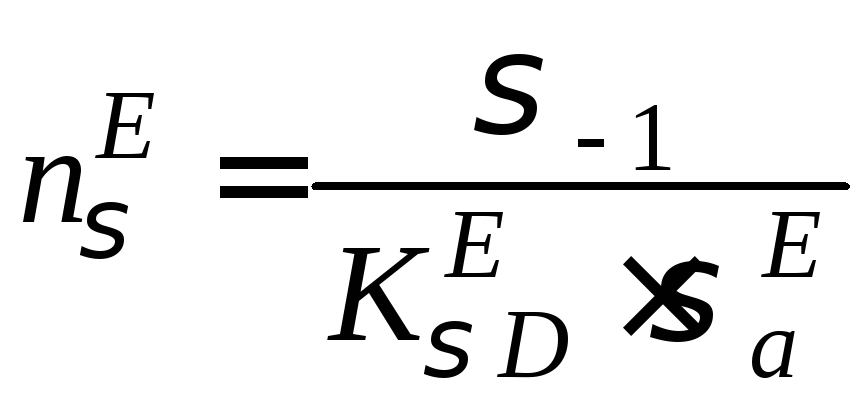 ,
,
![]() МПа.
МПа.
Тоді
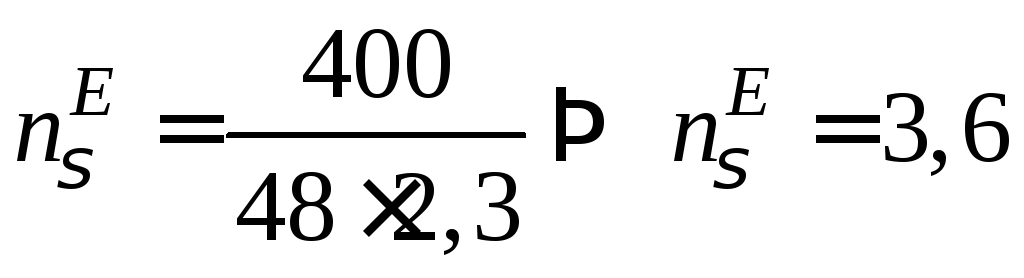 .
.
Оскільки
величина
![]() визначена з умови міцності матеріалу
в небезпечній точці перерізуЕ
при крученні, то
визначена з умови міцності матеріалу
в небезпечній точці перерізуЕ
при крученні, то
![]() ;
;
 .
.
Значить, коефіцієнт запасу вала
![]() .
.
Відповідь:
![]() ;n
=
2,05.
;n
=
2,05.
Питання до захисту розрахунково-графічної роботи (задача 14)
Який порядок розрахунку вала на витривалість при згині та крученні?
Як знаходяться максимальні і мінімальні величини крутних моментів?
Як визначаються небезпечні перерізи?
Як визначається амплітудне навантаження?
Як знаходиться полярний момент опору перерізу вала?
Як обчислюється коефіцієнт запасу міцності?
Як визначається величина допустимого зусилля?
