4.2 Завдання до розрахунково-графічної роботи

Задача 12. Проектний розрахунок на стійкість

Стрижень завдовжки l складного поперечного перерізу зазнає дії центрального стискального навантаження Р (рис. 4.6). Матеріал – сталь Ст. 3, основне допустиме напруження [σ_–] = 160 МПа.

Поперечний переріз стрижня прийняти згідно рис. 4.7. Схеми закріплення кінців стрижня в двох головних площинах подані в таблиці 4.1.

Необхідно:

• визначити раціональне розміщення перерізу щодо умов закріплення для подальшого розрахунок стояка на стійкість в площині мінімальної жорсткості;

• підібрати за сортаментом (додаток В) поперечний переріз стрижня, користуючись таблицями коефіцієнтів зниження допустимого напруження (додаток Е);

• обчислити критичну силу та запас по стійкості стрижня.

Увага! Умови закріплення приймати з таблиці 4.1

Рис. 4.6. Схеми закріплення кінців стержня

Таблиця 4.1

№ п/п	Р, кН	l, м	Спосіб закріплення кінців стояка
			Площина XOZ		Площина XOY
			Нижній кінець	Верхній кінець	Нижній кінець	Верхній кінець
0	300	8,5	защемлення	шарнір	шарнір	шарнір
1	350	8	защемлення	шарнір	шарнір	шарнір
2	400	7,5	шарнір	защемлення	шарнір	шарнір
3	450	7	шарнір	шарнір	защемлення	защемлення
4	500	6,5	защемлення	защемлення	защемлення	шарнір
5	550	6	защемлення	шарнір	шарнір	шарнір
6	600	5,5	шарнір	шарнір	защемлення	шарнір
7	650	3	защемлення	вільне	шарнір	шарнір
8	700	3,5	шарнір	шарнір	защемлення	вільне
9	750	4	шарнір	шарнір	защемлення	шарнір

Рис. 4.7. Схеми до виконання задачі 12

Приклад виконання задачі 12

Стрижень завдовжки l = 6 м зазнає дії центрального стискального навантаження Р = 800 кН. Матеріал стержня – сталь Ст. 3. Основне допустиме напруження [σ_–] =160 МПа. Підібрати за сортаментом поперечний переріз стрижня, що складається з двох жорстко з’єднаних між собою двотаврів (рис. 4.8, б).

Схеми закріплення кінців стрижня в двох головних площинах показані на рисунку (рис. 4.8, а). Розрахунок виконати для раціонального розміщення перерізу щодо закріплення. Обчислити запас по стійкості стрижня.

Розв’язування

Коефіцієнти умов закріплення стрижня згідно рис. Е.1 додатку Е

.

1. Перша спроба

Задаємось φ₁ = 0,5; потрібна площа поперечного перерізу (брутто)

м² = 100 см².

Рис. 4.8. Схеми до прикладу задачі 12

Потрібна площа одного двотавра

см²,

де 2 - кількість однакових двотаврів.

За сортаментом (додаток В) вибираємо двотавр №30а з такими геометричними характеристиками: площа А = 49,9 см², раді­ус інерції i_z = 12,5 см, ширина полиці см, момент інерціїсм⁴.

Вибираємо раціональне розміщення перерізу

Розміщуємо переріз так, як вказано на рис. 4.8, б.

Визначаємо радіус інерції відносно осі у

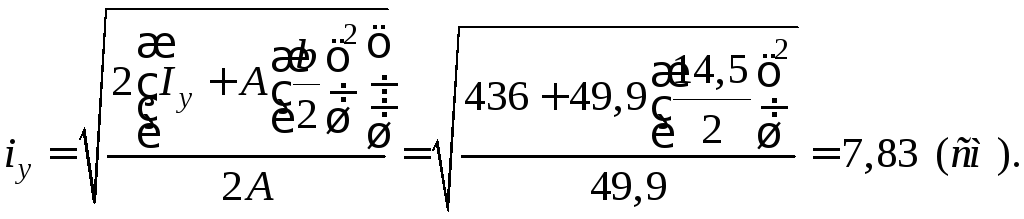
Гнучкість стрижня в двох головних площинах

;

;

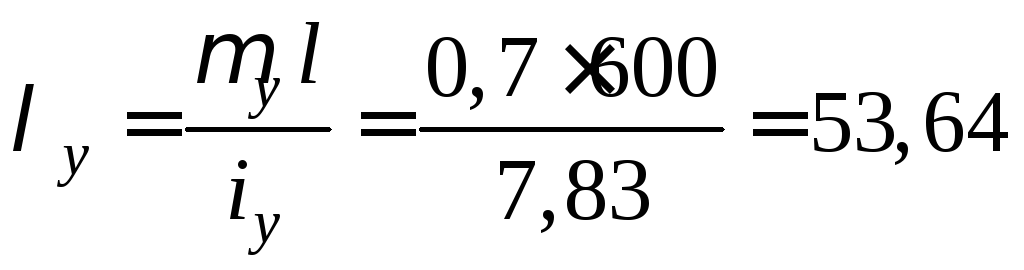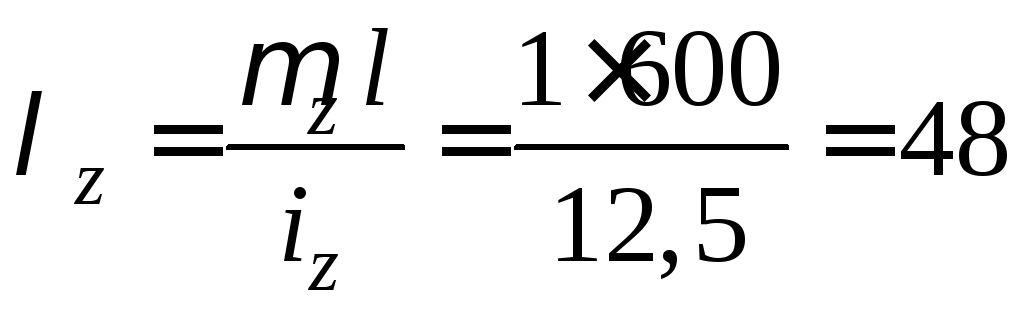, отже розрахунок при такому виборі закріплення необхідно проводити по осі у (в площині хоz).

Розміщуємо переріз так, як вказано на рис. 4.8, в.

В такому випадку раді­уси інерції i_у = 12,5 см, i_z = 7,83 см.

Гнучкості стрижня

;

;

.

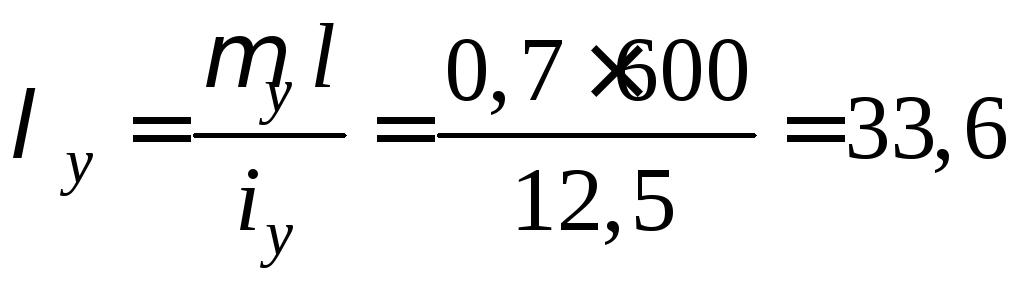Оскільки  , то розміщення перерізу у випадку, показаному на рис.4.8, б буде раціональним. Отже подальший розрахунок будемо проводити саме для такого закріплення.

Вказівка. Раціональному розміщенню переріза завжди буде відповідати така умова: якщо тоі якщото.

Таким чином, при за табл. Е.1 (додаток Е) при лінійній інтерполяції

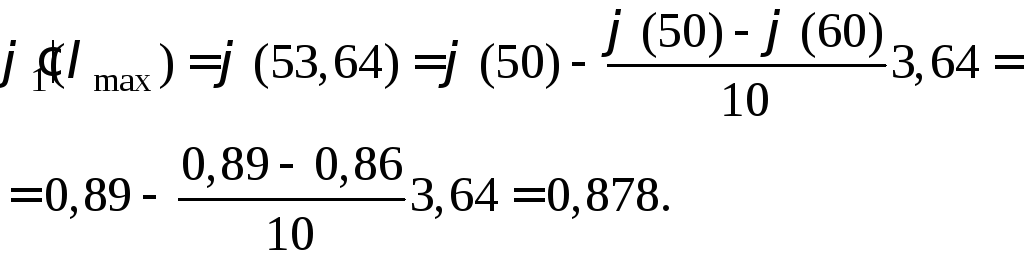
Оскільки »φ₁ = 0,5, то будемо проводити подальші уточнення. (Розв’язок вважається приблизно знайденим, якщо розбіжність між цими величинами складає не більше 5% від більшого значення)

2. Друге наближення

Приймаємо

.

Потрібна площа поперечного перерізу

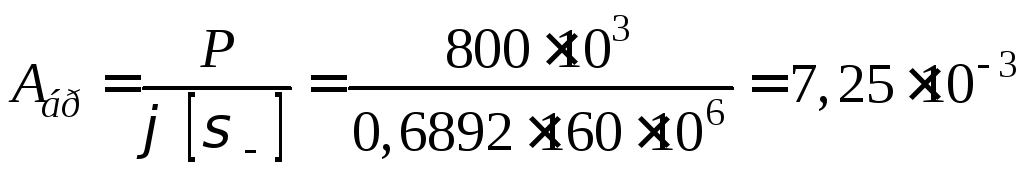м² = 72,5 см².

Потрібна площа одного двотавра

см².

За сортаментом вибираємо двотавр №24а з такими геометричними характеристиками: площа А = 37,5 см², раді­ус інерції i_z = 10,1 см, ширина полиці см, момент інерціїсм⁴.

Визначаємо радіус інерції відносно осі у

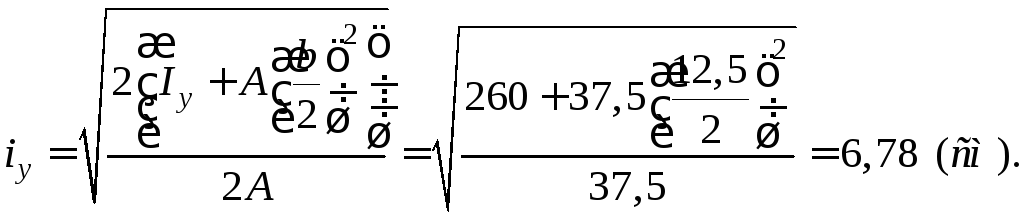
Гнучкість стрижня в двох головних площинах

;

;

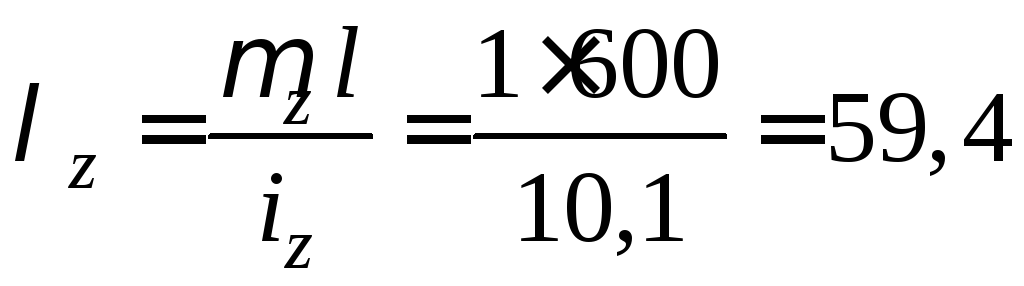, отже розрахунок проводимо по осі у.

При при лінійній інтерполяції

.

Оскільки » φ₂ = , то будемо в той самий спосіб проводити подальші уточнення.

Для наочності подальші наближення, разом із попередніми зведемо в таблицю 4.2.

Таблиця 4.2

№ п/п	Величина	Наближення
		перше	друге	третє	четверте
1		= 0,5	0,6892	0,7698	0,8034
2	, см2	100	72,5	64,95	62,23
3	, см2	50	36,25	32,48	31,23
4	Двотавр, номер	30а	24а	22а	22
5	А, см2	49,9	37,5	32,8	30,6
6	, см	7,83	6,78	6,502	5,948
7	iz , см	12,5	10,1	9,22	9,13
8		53,64 =	61,98 =	64,592	70,61=
9		48,78	59,4	65,08 =	65,71
10		0,878	0,8504	0,837	0,8063

Вказівка.

Зверніть увагу на монотонне зростання або спадання розрахункових величин в таблиці в кожному рядку. Це ознака правильності проведення наближень. Якщо на черговому наближенні порушується така тенденція, то слід переглянути розрахунки саме на цьому етапі. Особливо це стосується перерізів, що складаються з кутиків, оскільки необхідній площі відповідають декілька кутиків з різними радіусами інерції. В цьому випадку необхідно прийняти інший розмір переріза та повторити наближення.

Бачимо, що в останньому наближенні  φ₄ = .

Обчислимо еквівалентні напруження:

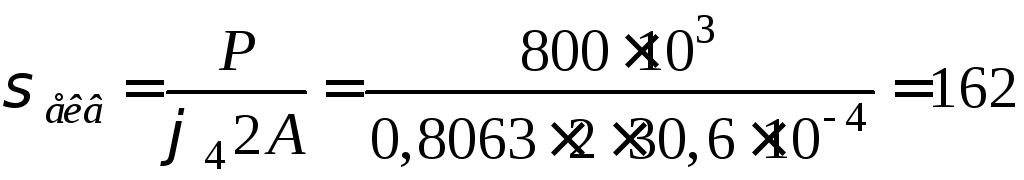МПа.

Перенапруження становить

.

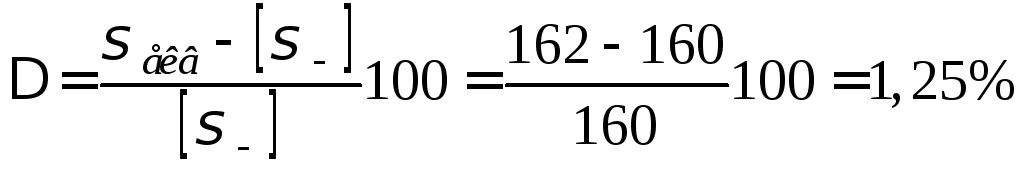
Допустиме значення перенапруження .

Вказівка.

Інколи два сусідніх за сортаментом переріза дають перенапруження і недонапруження, що перевищує допуск в 5%, тоді залишають переріз з недонапруженням, пояснивши вибір.

3. Визначаємо запас по стійкості

Оскільки 61  100, де 61 та 100 граничні значення гнучкості для сталі Ст. 3 (табл. Е.2, додаток Е), то критичне напруження визначаємо з формули Ясинського

МПа.

Критична сила

(Н).

Коефіцієнт запасу по стійкості

.

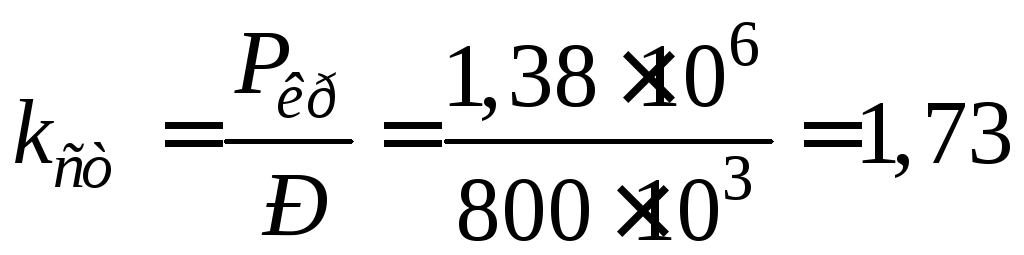Відповідь: Двотавр №22, .

Питання до захисту розрахунково-графічної роботи (задача 12)

1. За яким алгоритмом підбирається переріз стиснутого стержня (із використанням коефіцієнта зниження допустимого напруження)?

2. Чому при проектному розрахунку використовують послідовні наближення?

3. Записати формулу Ейлера та пояснити її.

4. Записати формулу розрахунку гнучкості та пояснити її.

5. Записати умову стійкості стержня із використанням коефіцієнта зниження допустимого напруження та пояснити її.

6. В яких випадках критичні напруження розраховуються за формулою Ейлера (границі застосування формули Ейлера)?

7. В яких випадках критичні напруження розраховуються формулою Ясинського?

8. В яких випадках можна говорити про раціональне розміщення перерізу щодо умов закріплення? Якій умові відповідає це розміщення?

9. Чому при розрахунку на стійкість приймають до уваги лише максимальну гнучкість?

10. Що називається критичною силою?

11. Що таке запас по стійкості та як він визначається для заданого стержня і навантаження? Які орієнтовні значення запасу для різних конструкційних матеріалів?