3.1.3 Визначення переміщень у статично невизначуваних системах

Визначивши зайві невідомі зусилля, переміщення в статично невизначуваних системах можна знайти звичайними способами. При цьому слід користуватися методами, які в кожному окремому випадку найбільш про­сто приводять до результату. Наприклад, прогини та кути повороту пере­різів статично невизначуваних балок, що несуть складне навантаження, зручно визначати за методом початкових параметрів. Спосіб Мора, що є універсальним, може застосовуватися в усіх випадках. Ним широко ко­ристуються при визначенні переміщень у балках, рамах, фермах.

Обчислюючи переміщення за формулою Мора

. (3.4)

слід розглянути задану систему під дією навантаження (остаточні епюри силових факторів М, N та Q статично невизначуваної системи), а також під дією одиничного силового фактора, що відповідає шуканому переміщенню (одиничні епюри ,,). Якщо при цьому одиничні навантаження прикладати безпосередньо до заданої статично невизначуваної системи, то кожен раз для побудови одиничних епюр ,,зно­ву доведеться розв'язувати статично невизначувану задачу. Однак цього можна уникнути, якщо врахувати, що вихідна статично невизначувана система й основна статично визначувана, навантажена заданими силами та знайденими зайвими невідомими, повністю тотожні за умовами роботи. Тому, визначаючи будь-яке переміщення, ми маємо право прикладати оди­ничне навантаження до основної статично невизначуваної системи. Ос­тання може бути вибрана за будь-яким можливим варіантом.

Як приклад обчислимо взаємні переміщення точок А_1­, А­₂ та В₁, В₂ відповідно в горизонтальному та вертикальному напрямах для рами (рис. 3.8, а).

Визначимо лише переміщення, спричинені згинанням, оскіль­ки переміщеннями від поздовжніх деформацій та зсуву можна знехтува­ти. На рис. 3.8, б наведено складові сумарної епюри згинальних моментів у вигляді, зручному для застосування способу Верещагіна.

Для визначення взаємного переміщення в горизонтальному напрямі точок А_1­, А­₂ прикладаємо до основної системи в цих точках (рис. 3.8, в) одиничні сили . Перемножуючи епюриМ та і вважаючи, що l₁ = l₂ = l знаходимо

.

Щоб визначити взаємне вертикальне переміщення точок В₁ та В₂, прикладаємо до основної системи в цих точках дві одиничні сили (рис. 3.8,г). Перемножуючи епюри М та , знаходимо, що

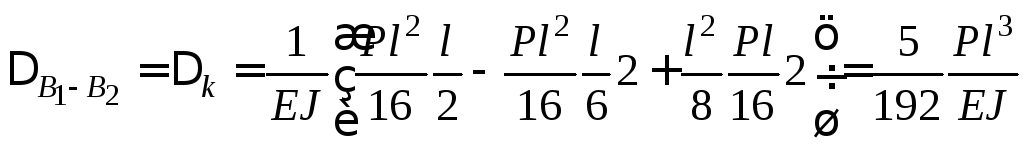
3.1.4 Контроль правильності розв'язання статично невизначуваної системи

Остаточні епюри N, Q та М обов'язково треба перевірити. Пере­віряють при цьому умови рівноваги та деформацій.

Для перевірки умов рівноваги слід вирізати вузол або яку-небудь части­ну системи й переконатися в її рівновазі, тобто у виконанні умов рівності нулю суми проекцій або моментів усіх зовнішніх та внутрішніх сил, при­кладених до цієї частини:

; ;.

При цьому потрібні величини слід брати безпосередньо з остаточних епюр.

Розглянемо, наприклад, як мають бути перевірені умови рівноваги для епюри згинальних моментів, наведеної на рис. 3.9. Виріжемо вузли В та С (рис. 3.10). Дію відкинутих частин рами на вузли замінимо відповідно згинальними моментами М_ВА, М_ВС, М_ВЕ та М_СВ, М_CD. Напрями мо­ментів відповідають розміщенню епюр на стиснутих волокнах.

З умов рівноваги вузла В випливає, що

.

З умови рівноваги вузла С випливає, що моменти М_СВ та М_CD ма­ють бути однаковими за модулем та протилежні за напрямом. Аналогіч­но можна перевірити епюри N та Q.

Зазначимо, що перевірка умов рівноваги не є достатньою, оскільки перевірка правильності побудови епюр за знайденими значеннями зайвих невідомих зусиль не дає підстав для міркування про правильність самих величин.

Загальним контролем є перевірка виконання умов нерозривності деформацій. При цьому слід переконатися, що остаточні епюри узгоджуються з умовами опорних закріплень та нерозривності контуру.

Оскільки в заданій статично невизначуваній системі переміщення в напрямі будь-якого зайвого зв'язку дорівнює нулю, то добуток остаточної епюри згинальних моментів на епюру моментів якого завгодно і-го стану основної системи має дорівнювати нулю, тобто

.

Як основну систему і-го стану найкраще вибирати систему, відмінну від взятої при розрахунку. Кількість перевірок умов деформацій має дорівнювати кількості зайвих зв'язків.

Оскільки при розрахунку системи зайві невідомі обчислюються з певною точністю, то й результати перевірки, звичайно, мають деяку похибку – шукані переміщення не дорівнюють нулю. Тому при перевірці рекомендується окремо обчислювати суми додатних та від’ємних членів. Якщо різниця між обома сумами, виражена у відсотках до меншої з них, невелика (до 5%), то результат розрахунку можна вважати задовільним.