3.1.2 Канонічні рівняння (canonical equations) методу сил

Додаткові рівняння переміщень, що виражають рівність нулю переміщень у напрямах зайвих невідомих, зручно складати в так званій канонічній формі, тобто за певною закономірністю.

Спочатку розглянемо систему один раз статично невизначувану (рис. 3.6, а). Як зайву невідому виберемо шарнірно-рухому опору В. Тоді, навантаживши основну систему заданим навантаженням і зайвою невідо­мою силою Х₁ (рис. 3.6, б) отримаємо рівняння

, (3.2)

де Δ_1Р – переміщення від заданого навантаження (рис. 3.6, в);

δ₁₁ – переміщення в напрямі Х₁ від сили (рис. 3.6, д),

Це канонічна форма рівняння переміщень для один раз статично невизначуваної системи. З формули (3.2)

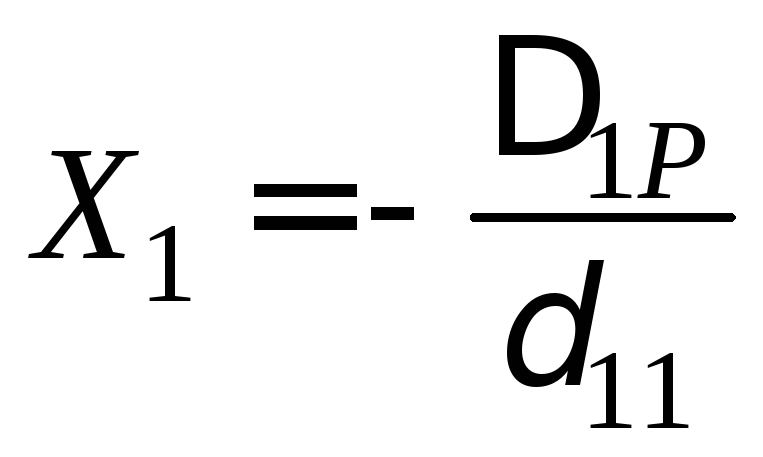, (3.3)

або, обчислюючи переміщення δ₁₁ та Δ_1Р, викори­стовуючи формулу Верещагіна і дані рис. 3.6, г, е, матимемо

;

.

Підставивши ці дані у формулу (3.3), остаточно знайдемо

.

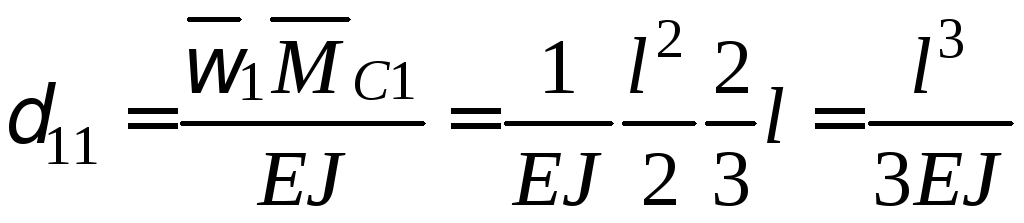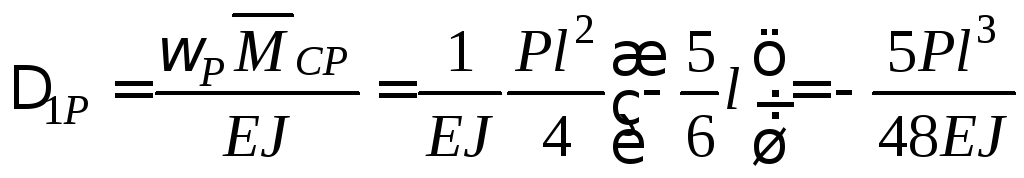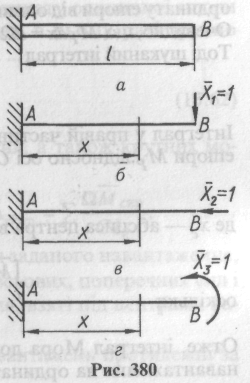
Для системи з двома зайвими зв'язками, як, наприклад, на рис. 3.7, а, б матимемо

;

.

Це канонічна форма рівнянь переміщень для системи двічі статично невизначуваної.

За аналогією можна записати в канонічній формі рівняння переміщень для будь-якої п разів статично невизначуваної системи:

;

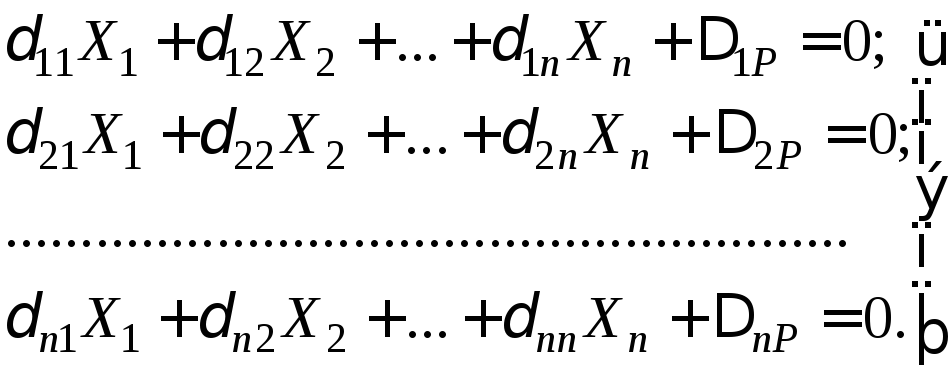ПереміщенняΔ_іР та δ_ik, що входять до канонічних рівнянь, найчасті­ше визначають за методом Мора або способом Верещагіна. При цьому для балок та рам впливом поперечних та поздовжніх сил, як правило, нехтують і враховують лише згинальні моменти. Однак, визначаючи пе­реміщення в балках прямокутного поперечного перерізу, для яких відно­шення висоти перерізу до довжини прогону h/l ≥ 1/5, поперечні сили вра­ховувати обов'язково. При розрахунку статично невизначуваних рам з великими зазначеними відношеннями (h/l > 1/5) похибка, спричинена неврахуванням інтегралів поздовжніх та поперечних сил, також може ста­ти істотною, особливо для високих рам. Слід мати на увазі, що в реальних балкових, рамних та арочних конструкціях відношення h/l, як правило, менше за 1/10. Тому при обчисленні переміщень у загальній формулі Мора цілком допустимо зберегти інтеграл, що враховує лише згинальні моменти.

Для визначення переміщень будуємо епюри згинальних моментів (див., наприклад, рис. 3.6) в основній системі окремо від заданого навантажен­ня (стан Р) і від кожної одиничної сили: (стан 1);(стан 2);…,(станn). Ординати відповідних епюр позначимо, як звичайно, через М_р, ,, …, . Тоді на підставі формули (3.9) знаходимо

; ; …;.

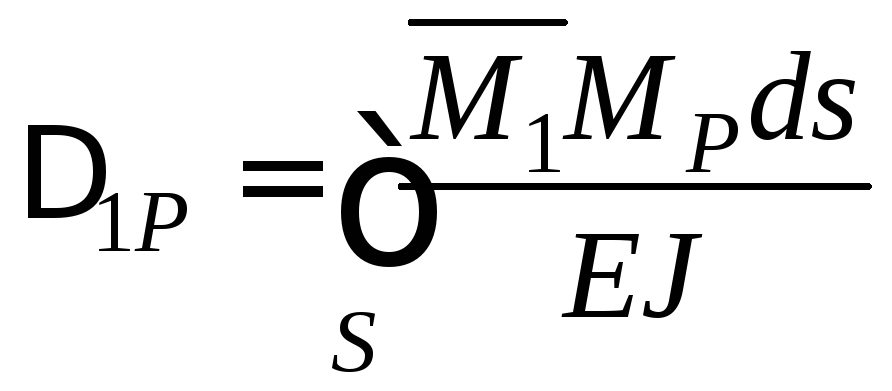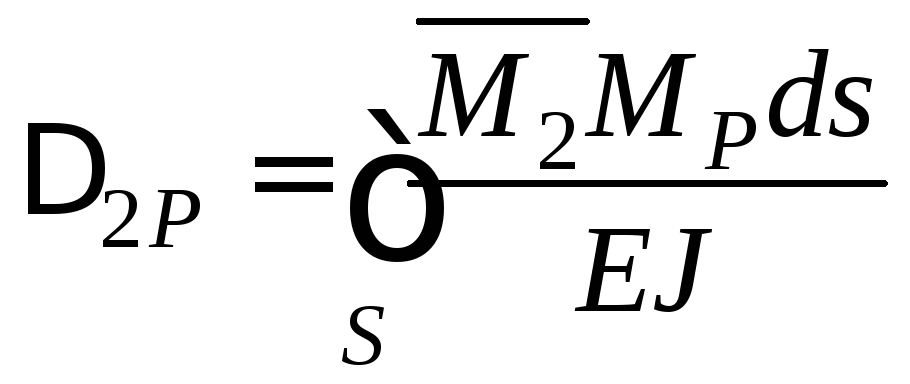Питомі переміщення, що мають однакові індекси й називаються голов­ними коефіцієнтами канонічних рівнянь, визначають так:

; ; …;.

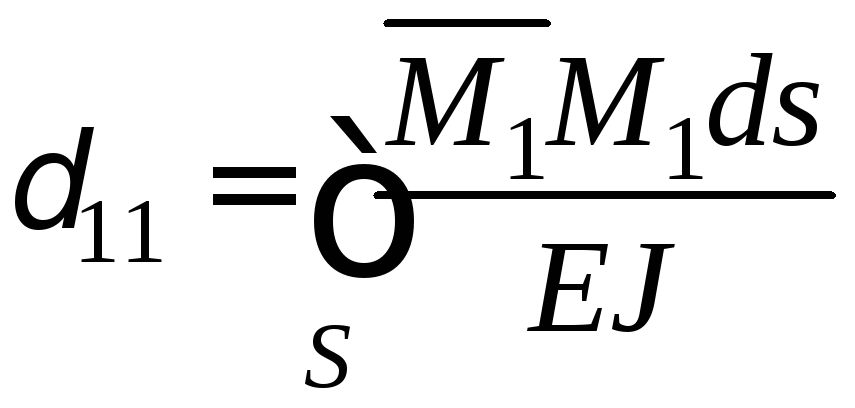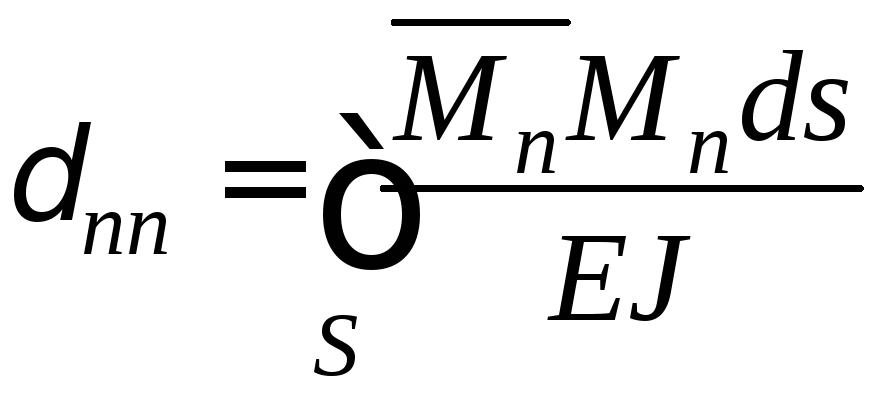Очевидно, що ці переміщення додатні.

Питомі переміщення, в яких індекси неоднакові, називають побічними коефіцієнтами й визначають за формулами

; ; …;.

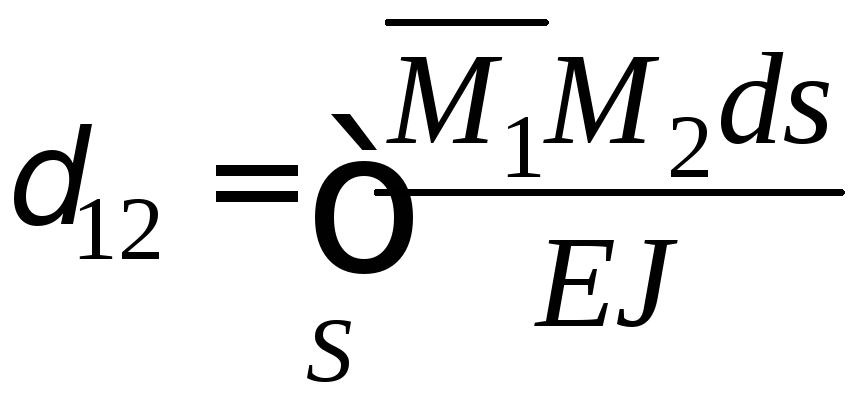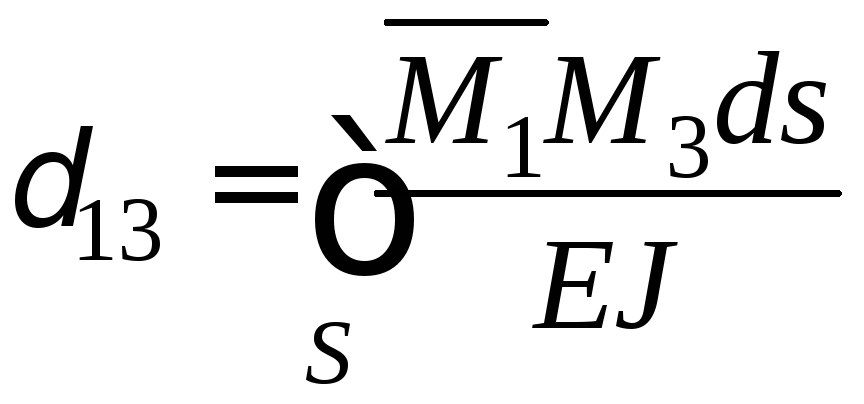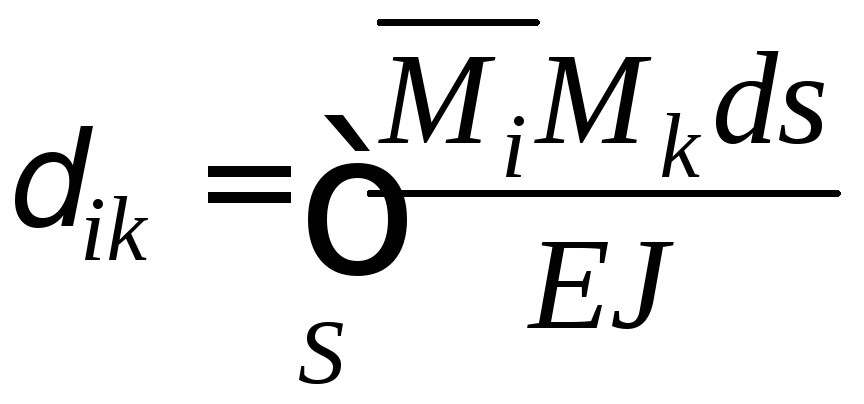Вони можуть бути додатними або від'ємними, а також дорівнювати нулю.

На підставі теореми про взаємність переміщень δ_ik = δ_ki.

Для систем, що складаються з прямолінійних елементів, обчислювати переміщення зручно за способом Верещагіна. Наприклад, для статично невизначуваної балки, зображеної на рис. 3.6:

; ;;

; ;.

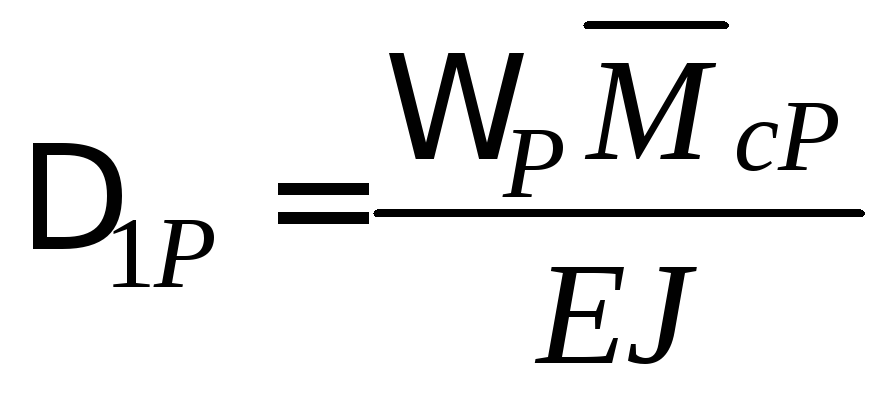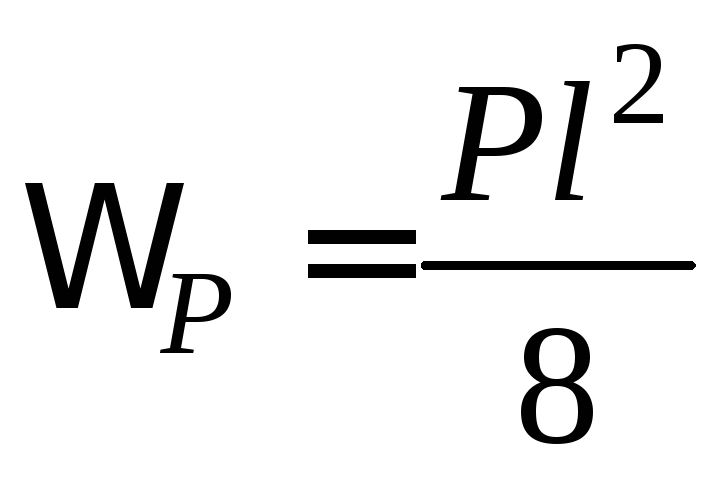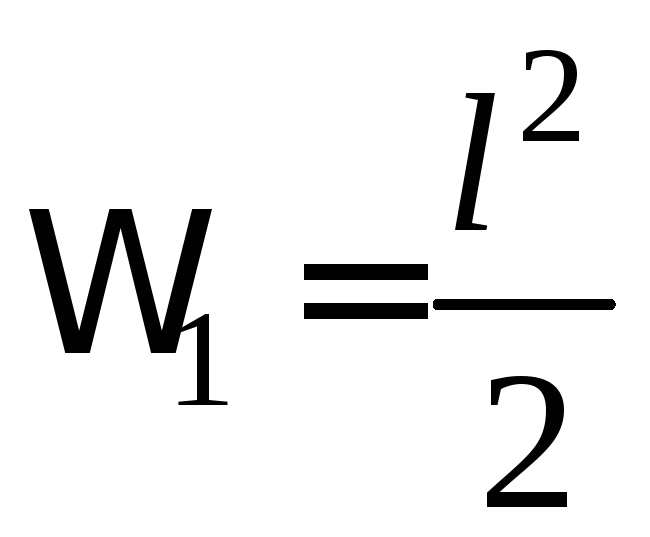Отже,

; .

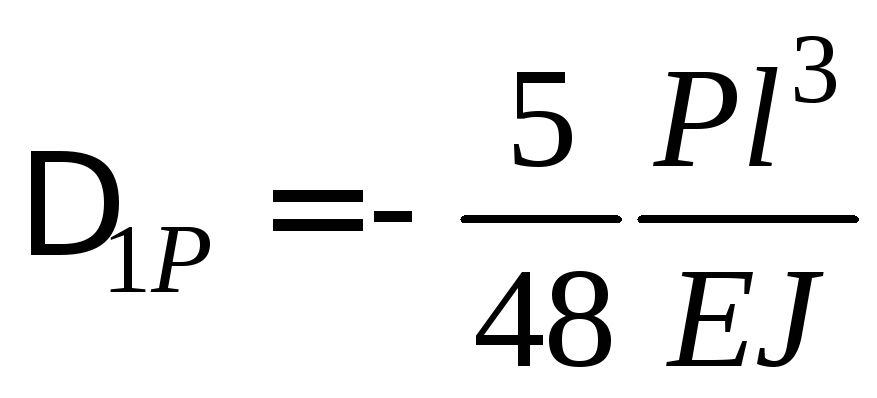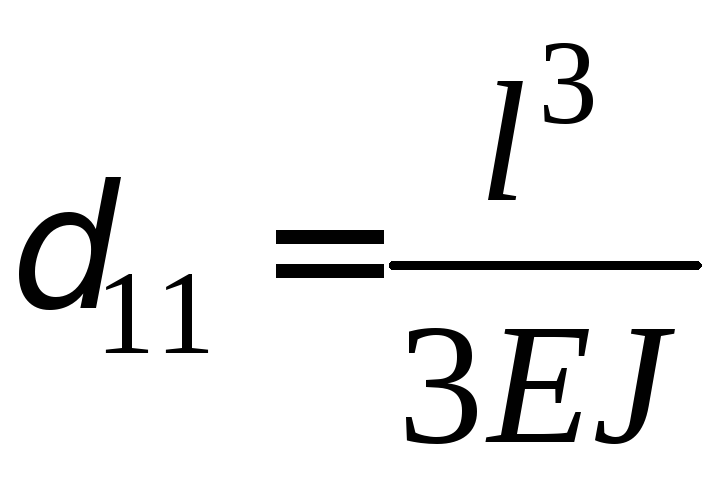З формули (3.3)

.