Теорема 2. Пусть ,,.

Если , то отображениеF сжимающее в метрическом пространстве и коэффициент сжатия его в этом пространстве равен.

Если , то отображениеF сжимающее в метрическом пространстве и коэффициент сжатия его в этом пространстве равен.

Если , то отображениеF сжимающее в метрическом пространстве и коэффициент сжатия его в этом пространстве равен.

Доказательство. Докажем первое утверждение теоремы. Зададим два произвольных столбца и рассмотрим

.

Здесь – элементы матрицыС.

и, следовательно, для любого номера j должно выполняться неравенство . Поэтому, заменив в последней сумме каждый из модулейвеличиной, получим

. Первое утверждение доказано. Остальные два утверждения теоремы доказываются аналогично.

Из доказанной теоремы следует, что метод простой итерации можно применять только к таким системам (3.4.1), у которых элементы матрицы С удовлетворяют хотя бы одному из условий теоремы (). А для выполнения этих условий необходимо, чтобы элементы матрицыС по модулю были достаточно малы. По крайней мере, их модули должны быть меньше 1. Это довольно жесткие ограничения, но их можно ослабить, так как линейная система стандартного вида приводится к виду (3.4.1) разными способами, причем каждый раз получается другая система с другой матрицей. Поэтомупрежде чем применить метод простой итерации к решению системы ее приводят к виду так, чтобы элементы матрицы С были по модулю как можно меньше. Это можно сделать следующим образом. Вначале расширенная матрица системы преобразуется с помощью элементарных преобразований (см. параграф 3.1) так, чтобы на главной диагонали матрицы А стояли самые большие по модулю элементы матрицы (преобладающие). Чем сильнее будет диагональное преобладание, тем лучше. Затем записывается линейная система, соответствующая преобразованной расширенной матрице. Эта система будет, очевидно, равносильна исходной системе. Далее из первого уравнения этой системы выражается первая переменная , из второго – вторая переменнаяи так далее. В результате получается линейная система вида ,причем все элементы матрицы С будут по модулю меньше 1.

Описанная методика не гарантирует, что будет выполнено хотя бы одно из условий теоремы 2. Все зависит от того, насколько сильного диагонального преобладания удастся добиться в процессе преобразования расширенной матрицы. Проиллюстрируем ее на примере.

Пример.

Привести линейную систему

к виду, удобному для применения метода простой итерации.

Запишем расширенную матрицу этой системы и с помощью элементарных преобразований будем добиваться того, чтобы на главной диагонали матрицы стояли преобладающие по модулю элементы:

.

Здесь жирным шрифтом показаны преобладающие по модулю диагональные элементы. Для того чтобы можно было надеяться на выполнение первых двух условий теоремы 2, необходимо, чтобы на главной диагонали стояли самые большие по модулю числа в своих строках и столбцах матрицы А и модули этих чисел были больше сумм модулей элементов, стоящих в соответствующих строках или столбцах. Это условие в нашем случае выполняется. Запишем теперь линейную систему, соответствующую преобразованной расширенной матрице:

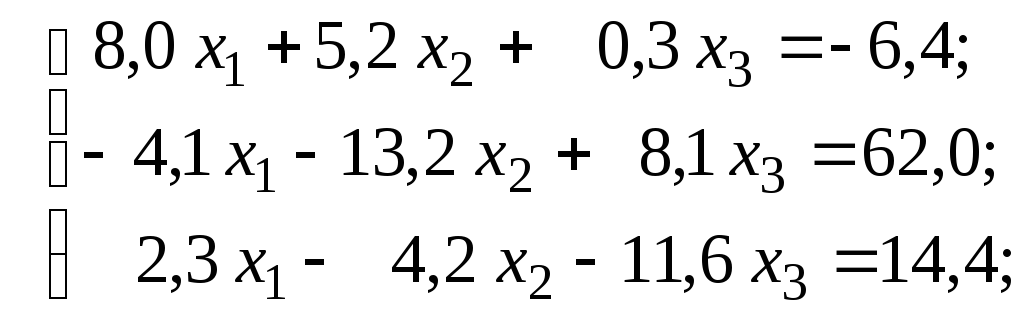
и выразим соответствующие переменные из соответствующих строк:

В результате мы получили систему вида с матрицами

, .

Осталось убедиться, что выполняется хотя бы одно условие теоремы 2 и найти коэффициент сжатия отображения F в соответствующем метрическом пространстве. Найдем

0,93<1. Таким образом, можно применять метод простой итерации в пространстве с коэффициентом сжатия. Остальные условия можно и не проверять. Достаточно, чтобы выполнялось одно из условий, причем чем меньше коэффициент сжатия, тем быстрее сходимость.