3.5. Решение систем нелинейных уравнений Получение итерационной формулы метода касательных путем линеаризации уравнения

Метод касательных, рассмотренный в параграфе 2.4 и применяемый для решения уравнений с одним неизвестным

, (3.5.1)

нередко называют методом Ньютона или методом линеаризации. Это связано с тем, что итерационную формулу метода касательных можно получить путем линеаризации уравнения (3.5.1). Кроме того, метод Ньютона, применяемый для решения систем нелинейных уравнений, является прямым обобщением метода касательных. Поэтому прежде чем приступать к изучению метода Ньютона для систем уравнений полезно будет в начале подробнее рассмотреть некоторые аспекты работы метода касательных, которых мы не касались ранее.

Пусть– точное значение искомого корня уравнения (3.5.1). Для получения приближенного решенияуравнения (3.5.1) с заданной точностьюпостроить последовательность приближенийтакую, что. Пусть известенn-й член последовательности . Для построения следующего членалинеаризуем уравнение (3.5.1), то есть линеаризуем функцию , входящую в это уравнение, заменив ее приближенно линейной функцией. Для этого используем многочлен Тейлора первой степени

. (3.5.2)

Геометрический смысл такой замены состоит в том, что график функции заменяется касательной, проведенной в точке. Подставим формулу (3.5.2) в формулу (3.5.1) и после очевидного преобразования получим приближенное уравнение вида

. (3.5.3)

Корень линеаризованного уравнения (3.4.3)

(3.5.4)

можно интерпретировать как некоторое приближенное значение корня уравнения (3.5.1). Именно его и выберем в качестве следующего члена последовательности приближений :

. (3.5.5)

Таким образом, получили уже знакомую итерационную формулу метода касательных.

Скорость сходимости метода касательных

Для сравнения различных последовательностей приближений и различных итерационных методов решения уравнений с одной неизвестной вводится величина, называемая порядком сходимости последовательности приближений.

Пусть – последовательность приближений, сходящаяся к точному значению искомого корня. Если найдутся вещественное числои номертакие, что для всех номеровk, больших или равных , выполняется неравенство

, (3.5.6)

то говорят, что последовательность приближений имеет первый порядок сходимости или что она имеет линейную сходимость, или что она сходится со скоростью геометрической прогрессии. Последнее название легко понять. В самом деле, применяя формулу (3.5.6) последовательно для , получим

,

,

……………………………………………

при . (3.5.7)

Из формулы (3.5.7) следует, что погрешность приближения действительно стремится к 0 быстрее, чем геометрическая прогрессия со знаменателемq.

Линейную сходимость имеют последовательности приближений, получаемые методом простой итерации и методом половинного деления (для последнего ). Но существует и более быстрая сходимость.

Если найдутся вещественное число , вещественное числои номертакие, что для всех номеровk, больших или равных , выполняется неравенство

, (3.5.8)

то говорят, что последовательность приближений сходится к точному значению искомого корнясp-м порядком.

Чем больше порядок сходимости p, тем быстрее сходимость, причем при , в отличие от случая линейной сходимости, на величинуС не накладывается никаких ограничений. В самом деле, применяя формулу (3.5.8) последовательно для , получим

,

,

,

……………………………………………

.

Отсюда

. (3.5.9)

Из формулы (3.5.9) следует, что если находится настолько близко к корню, что выполняется неравенство

, (3.5.10)

то погрешность приближения действительно стремится к 0 при, причем быстрее, чем любая геометрическая прогрессия, поскольку, а. Чем больше величинаp, тем быстрее и, следовательно, тем быстрее сходимость.

Убедимся, что последовательность приближений, полученная методом касательных, при определенных условиях может иметь второй порядок сходимости. Для этого введем функцию . Каждый корень уравнения

(3.5.11)

будет корнем уравнения (3.5.1). Если , то верно будет и обратное утверждение. Таким образом, если, тобудет также и корнем уравнения (3.5.11), то есть будет справедливо равенство

. (3.5.12)

Итерационная формула метода касательных (3.5.5) может быть записана в виде

. (3.5.13)

Вычтем из равенства (3.4.13) равенство (3.4.12) и получим

. (3.5.14)

Разложим функцию по формуле Тейлора с остаточным членом в форме Лагранжа

.

Здесь – некоторая точка междуx и . Подставим в эту формулуи получим

Здесь  некоторая точка между и. Подставим это выражение в формулу (3.5.14) и получим

. (3.5.15)

При выводе формулы (3.5.15) мы воспользовались формулой Тейлора. А она справедлива, только если существует окрестность точки , в которой существует, а точкаx принадлежит этой окрестности. Таким образом, для того чтобы можно было использовать формулу (3.5.15), достаточно, чтобы существовала окрестность искомого корня , в которой существует, адолжна этой окрестности принадлежать. Найдем производные функции .

,

.

Таким образом, для существования второй производнойдостаточно, чтобы существовала третья производная и . Если корень простой (то есть если ) и существует окрестность этого корня, в которой существует, то производнаябудет непрерывна в этой окрестности. Тогда, согласно теореме о сохранении знака непрерывной функции, найдется окрестность точки, в которой. Следовательно,для применения формулы (3.5.15) достаточно, чтобы существовала окрестность искомого корня , в которой существует непрерывная производная, причем , а точка должна принадлежать окрестности точки ,в которой .

Дальнейшие рассуждения будем проводить в предположении, что это условие выполняется. Прежде всего убедимся, что

.

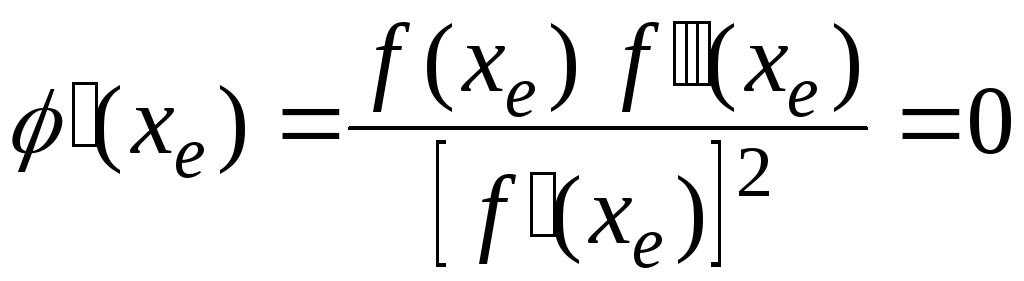Таким образом, формула (3.4.15) становится более постой:

.

Отсюда следует, что

. (3.5.16)

Из непрерывности следует, что будет существовать окрестность точки , в которой будет непрерывна и ограничена. Тогда, если точкапринадлежит этой окрестности, то найдется положительная постояннаяС такая, что в этой окрестности и будет справедливо неравенство

. (3.5.17)

Таким образом, метод касательных действительно имеет второй порядок сходимости при выполнении отмеченных условий.

Объединив полученные результаты, можно сформулировать достаточные условия квадратичной сходимости метода касательных. Если существует окрестность искомого корня , в которой определена непрерывная третья производнаяи первая производная, а начальное приближение принадлежит этой окрестности и удовлетворяет неравенству

, (3.5.18)

то последовательность приближений , полученная методом касательных, будет сходиться к искомому значению корня, причем сходимость эта будет квадратичной, то есть для любого номераn будет выполнено условие (3.5.17).

Остается отметить, что полученные условия квадратичной сходимости часто бывает нелегко проверить. Да и подбор начального приближения представляет собой нетривиальную задачу.