Обратный ход метода Гаусса. 1. Приближенная проверка невырожденности матрицы системы. Если , то выдать сигнал о том, что матрица системы близка к вырожденной и закончить решение системы.

2. Вычисление решения по рекуррентным формулам

,

, ,.

3.3. Метод правой прогонки Алгоритм решения линейной системы методом правой прогонки

Метод правой прогонки применяется для решения систем с трёхдиагональными матрицами и представляет собой модификацию метода Гаусса. Трехдиагональная матрица отличается тем, что ненулевые элементы могут стоять только на главной диагонали матрицы и двух соседних диагоналях. Все остальные элементы матрицы должны быть равны нулю. Приведем в качестве примера систему с трехдиагональной матрицей пятого порядка

. (3.3.1)

При обозначении элементов матрицы системы применяется нестандартная система обозначений. Обозначения введены только для отличных от нуля коэффициентов, причем коэффициенты, стоящие на главной диагонали, обозначены буквой С со знаком минус, а коэффициенты, стоящие на двух соседних диагоналях обозначены буквами А и В. Это позволяет существенно экономить память ЭВМ, не забивая ее огромным количеством никому не нужных нулей. Знаки минус, поставленные перед коэффициентами С и правыми частями F, появились из-за того, что мы будем использовать метод прогонки в дальнейшем, при решении разных других задач, и нам будет удобнее, если матрица системы во всех случаях будет иметь одинаковый вид.

Запишем произвольную систему с трехдиагональной матрицей (М-1)-го порядка в общем виде, используя описанную систему обозначений:

(3.3.2)

Система (3.3.1) эквивалентна системе (3.3.2) при М=6.

Если применить к решению системы (3.3.2) процедуру прямого хода метода Гаусса, то в результате получится система, матрица которой будет иметь две диагоналями: главную и правую. Разделим каждое уравнение преобразованной системы на диагональный элемент, стоящий в этой строке. В результате получится система с двухдиагональной матрицей, на главной диагонали которой стоят единицы. Эта система будет иметь вид (при M=6)

(3.3.3)

Тогда рекуррентные формулы обратного хода метода Гаусса примут вид

, (3.3.4)

причём

. (3.3.5)

Для определения коэффициентов изаменим в равенстве (3.2.4) величинуm на m-1:

(3.3.6)

и подставим в исходную систему (3.3.2):

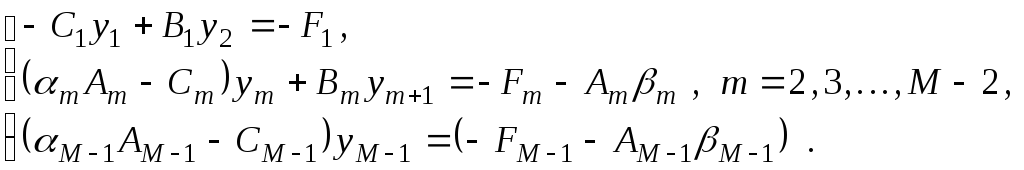
После элементарных преобразований получим

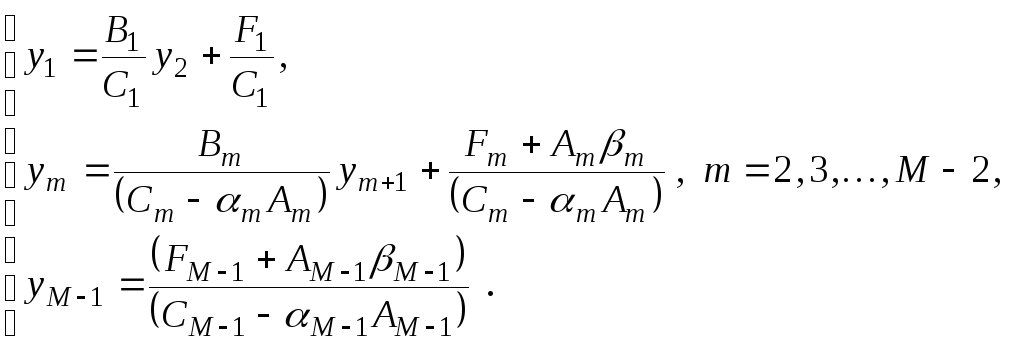
Сравнивая эти формулы с (3.3.4) получим

(3.3.7)

Введём фиктивные величины ,,,и. Положим

,,, (3.3.8)

тогда формулы (3.3.7) можно будет записать одной строкой:

(3.3.9)

Рекуррентные формулы (3.3.8) – (3.3.9) позволяют вычислить все неизвестные коэффициенты и. Для получения решения системы (3.3.2) используем рекуррентную формулу (3.3.4), но для начала счёта по ней необходимо знать значение. Поскольку(так как), значениеможно выбрать любое, например

. (3.3.10)

В результате получим алгоритм решения системы (3.3.2) методом прогонки: вначале по рекуррентным формулам (3.3.9) с начальными условиями (3.3.8) получим значения ,,,, … ,,, затем по рекуррентной формуле (3.3.4) с начальным условием (3.3.10) получим решение системы:.