Условия применимости метода прогонки

В процессе вычисления величин ипо формулам (3.3.9) происходит деление на величины, которые могут обращаться в ноль. В этом случае метод прогонки применять нельзя. Поэтому необходимо знать и предварительно проверять условия, при которых можно использовать этот метод. Достаточные условия применимости метода прогонки сформулируем в виде теоремы.

Теорема 1. Если

, ,

, ,

, ,,,

то дляи метод прогонки можно применять.

Доказательство. Неравенства длядокажем методом математической индукции.. Пусть при некоторомm выполняется неравенство , тогда

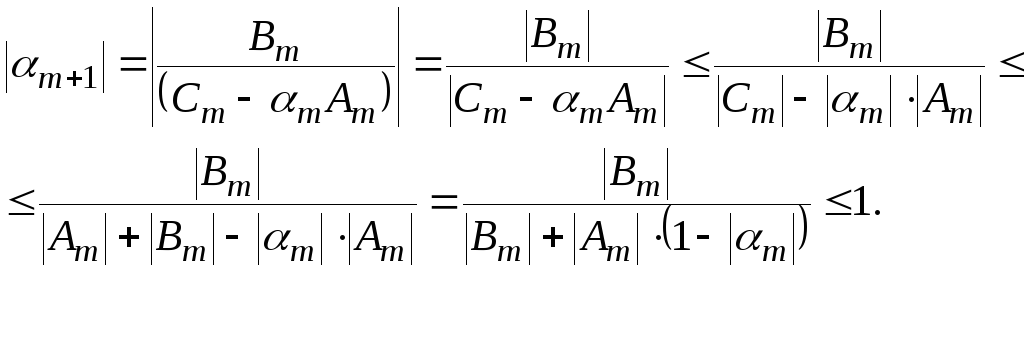
Неравенство доказано. Осталось доказать, чтопри. Зафиксируем любое из целых значенийи рассмотрим разность:

Отсюда . И наконец, рассмотрим два оставшихся случая:, так как.Теорема полностью доказана.

3.4. Метод простой итерации для линейных систем

Метод простой итерации применяется для решения линейных систем нестандартного вида, отличного от (3.1.1):

. (3.4.1)

Здесь C – заданная матрица порядка n, d – заданный столбец с n координатами, а x – искомый столбец. Но, очевидно, любую систему стандартного вида можно многими разными способами привести к равносильной системе вида (3.4.1) и наоборот. Будем решать систему (3.4.1) в предположении, что она имеет единственное решение.

Метод простой итерации основан на методе последовательных приближений и принципе сжимающих отображений (см. параграф 1.11 ). Введем отображение

. (3.4.2)

Тогда система (3.4.1) примет вид

. (3.4.3)

Аргумент x и значение y введенного отображения F представляют собой векторы с n координатами и, следовательно, принадлежат пространству , где можно ввести, по крайней мере, три метрики:,,.

Здесь и– координатами векторовx и y. Проверьте самостоятельно, что введенные функции ,и удовлетворяют всем аксиомам метрики. Таким образом, мы получаем три метрических пространства: ,,. Можно доказать, чтовсе эти метрические пространства являются полными.

Обозначим через любую из этих метрик, а черезлюбое из введенных метрических пространств. Точное решение системы (3.4.1) (и уравнения (3.4.3)) обозначим.Будем искать приближенное решение системы (3.4.1), ,абсолютная погрешность которого не превышает заданного положительного числа :

. (3.4.4)

Точное решение системы, представляет собой также неподвижную точку отображенияF. Поэтому для решения этой задачи можно воспользоваться теоремой о сжимающем отображении (см. теорему из параграфа 1.11). Так как метрическое пространство является полным,для выполнения условий указанной теоремы (принципа сжимающих отображений) достаточно, чтобы отображение F было сжимающим в метрическом пространстве .В этом случае, согласно принципу сжимающих отображений, последовательность столбцов , которая получается по рекуррентной формуле

, k=0, 1, … (3.4.5)

при любом начальном приближении будет сходиться к неподвижной точке отображенияF, совпадающей с точным решением нашей системы :

. (3.4.6)

Кроме того, из выполнения неравенства

(3.4.7)

_{следует выполнение неравенства}

_{. (3.4.8)}

Здесь  коэффициент сжатия отображения F в метрическом пространстве . Поэтому, как только неравенство (3.4.7) будет выполнено, в качестве искомого приближенного решения системы можно выбрать , и записать алгоритм решения системы (3.4.1) методом простой итерации.

Алгоритм. В качестве начального приближения обычно выбирают вектор d: . Далее по формуле (3.4.5) производится последовательное вычислениеи на каждом шаге этого цикла (при каждом значении) проверяется выполнение неравенства (3.4.7). И как только это неравенство выполнится, последний вычисленный член последовательностидаст нам искомое приближенное решение системы.

Но использовать этот алгоритм можно только тогда, когда отображение F является сжимающим в . А это выполняется далеко не всегда. Условия, при выполнении которых отображение F будет сжимающим в, приведены в следующей теореме.