Алгоритм вычисления определителя

Основу алгоритма вычисления определителя методом Гаусса составляет цикл, выполняемый последовательно для . Введем переменнуюd, которая по окончании вычислений примет значение искомого определителя. До начала цикла переменная d полагается равной 1. На k-м шаге цикла необходимо либо , если перестановка (обмен значениями)k-й и p-й строк не производится, либо , если перестановка производится, апо окончании цикла необходимо . Перестановка строк должна осуществляться при. Осталось записатьдействия, которые должны выполняться на k-м шаге цикла:

1. Определение главного элемента в k-м столбце, то есть вычисление числа М и номера строки p таких, что

.

2. Если , то производится обмен значениями элементовk-й и p-й строк (перестановка строк) матрицы и изменение знака d:

, ,

.

В противном случае, если , то.

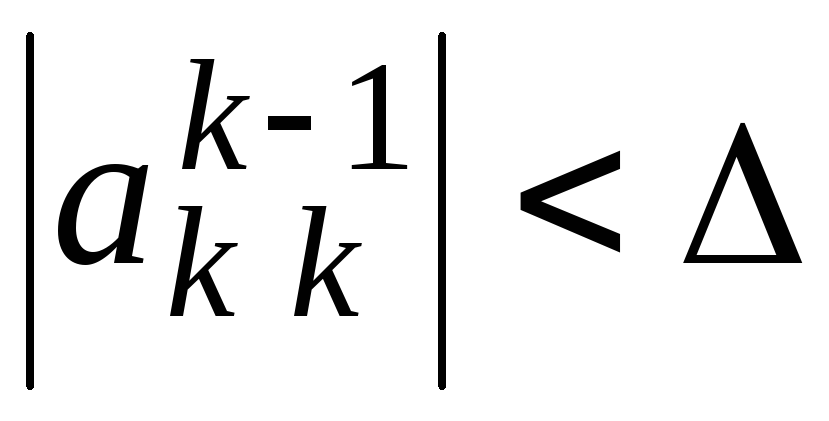3. Приближенная проверка равенства нулю определителя. Если , то следует выдать сигнал о том, что определитель приближенно равен нулю и закончить вычисление. Здесь–заданное маленькое положительное число, например, характеризующее точность вычисления нуля определителя. При выполнении условиямодули всехпритакже будут меньшеи определитель матрицы системы будет близок к нулю.

4. Деление k-й строки матрицы на :

, .

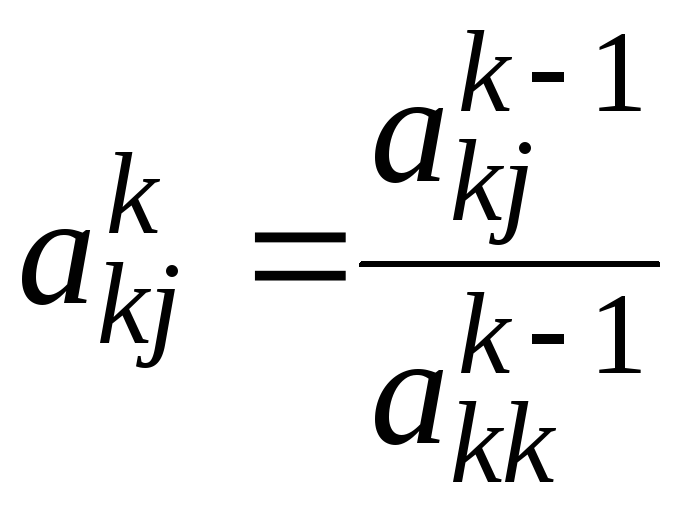5. Преобразования строк с номерами . Изi-й строки матрицы системы вычитается k-я строка, умноженная на :

, ,,

Применение метода Гаусса для вычисления обратных матриц Сведение вычисления обратной матрицы к решению линейной системы

Вычисление матрицы , обратной матрицеА n-го порядка, сводится к решению n линейных систем с одной и той же матрицей А и разными правыми частями. Поэтому для вычисления обратной матрицы можно использовать любой метод решения линейных систем, в том числе и метод Гаусса. По определению обратной матицы

, (3.2.14)

где Е – единичная матрица n-го порядка. Обозначим через  столбцы единичной матрицы Е,  столбцы матрицы . Тогда матричное равенство (3.2.14) можно переписать в виде эквивалентной системы равенств

. (3.2.15)

Обозначим через элементы искомой обратной матрицы, а черезэлементы единичной матрицыЕ n-го порядка. Очевидно,

, .

Таким образом, системы (3.2.15) можно записать в развернутом виде

. (3.2.16)

Для определения всех столбцов обратной матрицы необходимо решить все линейные системы (3.2.16). Поскольку у всех этих систем одна и та же матрица, прямой ход метода Гаусса можно проводить параллельно для всех систем сразу, что позволяет существенно уменьшить вычислительные затраты. Для этого мы введем расширенную матрицу систем вида

и с ней будем проводить преобразования прямого хода метода Гаусса.

Алгоритм вычисления обратной матрицы

Прямой ход метода Гаусса. Прямой ход метода Гаусса представляет собой цикл, выполняемый последовательно для . Верхние индексы элементов расширенной матрицы указывают на номер шага прямого хода, в результате которого получено значение этого элемента. Приведем алгоритм и расчетные формулы для k-го шага прямого хода метода Гаусса с выбором главных элементов в столбцах.

1. Определение главного элемента в k-м столбце, то есть вычисление числа М и номера строки p таких, что

.

2. Если , то производится обмен значениями элементов (перестановка)k-й и p-й строк расширенной матрицы

, .

, ,

3. Приближенная проверка невырожденности матрицы системы. Если , то следует выдать сигнал о том, что матрица системы близка к вырожденной и закончить решение системы. Здесь– заданное маленькое положительное число, например. При выполнении условиямодули всехпритакже будут меньшеи определитель матрицы системы будет близок к нулю.

4. Деление k-й строки расширенной матрицы на :

, ,

, .

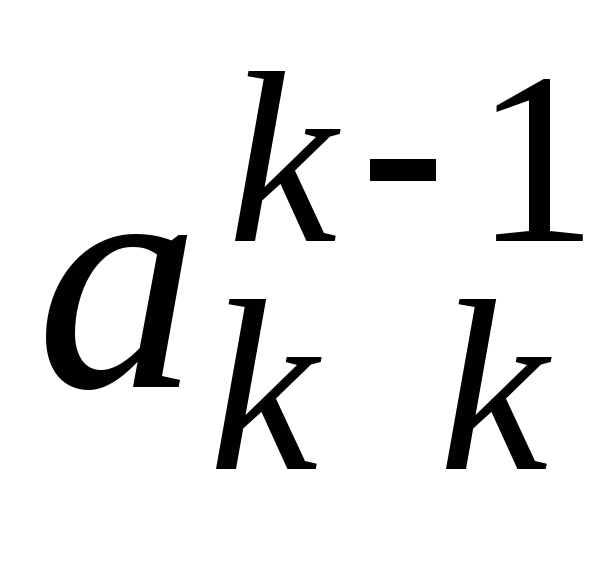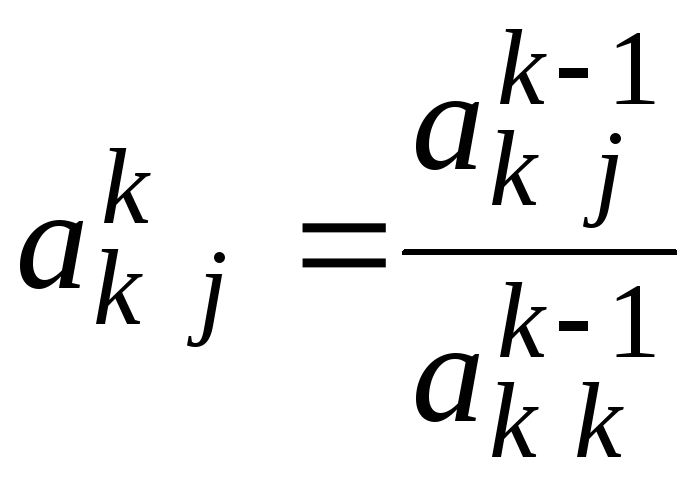5. Преобразования строк с номерами . Изi-й строки расширенной матрицы системы вычитается k-я строка, умноженная на :

, ,,

, ,.