Обратный ход метода Гаусса

Запишем линейную систему, получившуюся в результате прямого хода метода Гаусса, с расширенной матрицей, приведенной в табл. 3.3.:

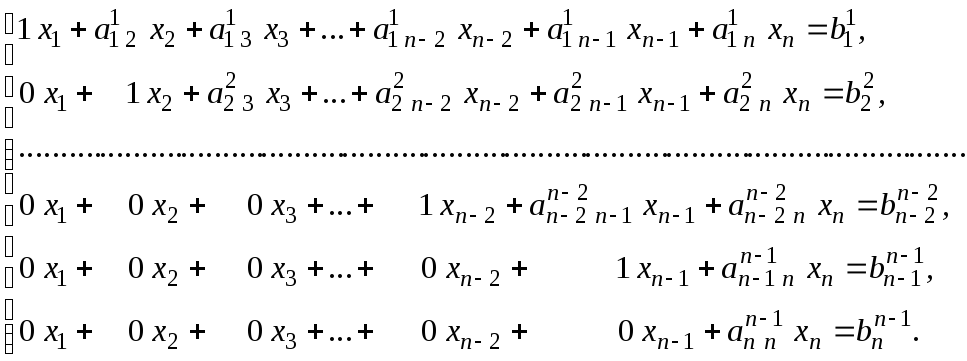(3.2.10)

Система (3.2.10) равносильна исходной системе (3.2.1) и ее решение получить несложно. Из последнего уравнения системы можно сразу найти , из предпоследнего , и т. д.

Алгоритм и расчетные формулы для обратного хода метода Гаусса

1. Приближенная проверка невырожденности матрицы системы. Если 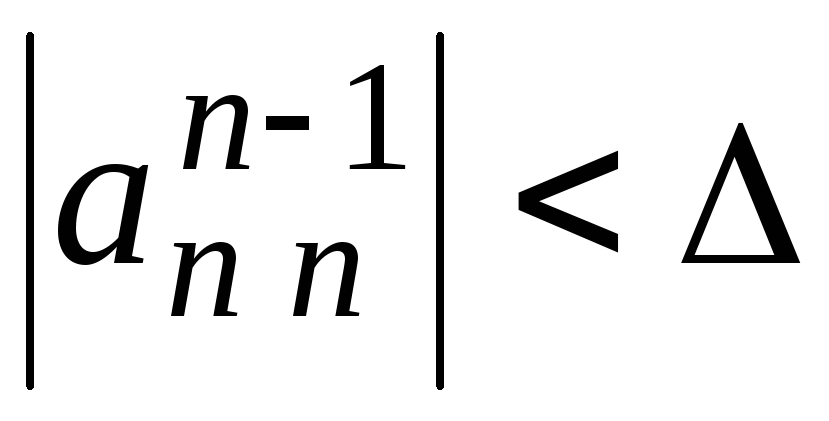, то выдать сигнал о том, что матрица системы близка к вырожденной и закончить решение системы. При выполнении условиямодуль определителя матрицы системы будет меньшеи близок к нулю.

2. Вычисление решения по рекуррентным формулам

, (3.2.11)

, . (3.2.12)

На этом можно было бы завершить алгоритмическую схему метода Гаусса с выбором главных элементов в столбцах. Осталось только сделать последнее замечание. В процессе обратного хода метода Гаусса используются только элементы матрицы, стоящие выше главной диагонали и . Нули, стоящие под главной диагональю, и единицы, стоящие на главной диагонали, для получения решения не нужны. Поэтому их можно не вычислять. А для того чтобы не делать эти лишние операции, можно исключить из алгоритма прямого хода вычисления по формулам (3.2.6), (3.2.8) при .

Применение метода Гаусса для вычисления определителей Теоретические основы

При вычислении определителя квадратной матрицы А можно использовать прямой ход метода Гаусса. Применение метода Гаусса для вычисления определителей основано на их свойствах:

1. Если поменять местами две строки матрицы, то ее определитель поменяет свой знак, а абсолютная величина определителя не изменится .

2. Если какую-либо строку матрицы разделить на некоторую постоянную с, не равную нулю, то определитель матрицы уменьшится в с раз .

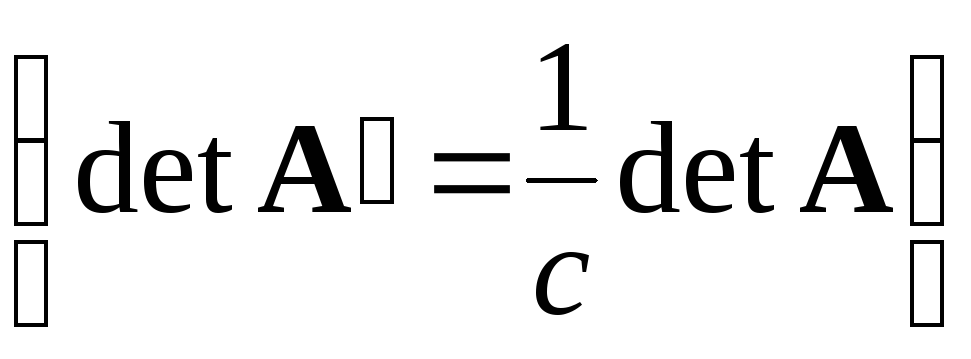3. Если из какой-либо строки матрицы вычесть другую строку, умноженную на некоторое число, не равное нулю, то определитель не изменится .

4. Если матрица является верхней треугольной (все ее элементы, лежащие ниже главной диагонали, равны 0), то её определитель будет равен произведению диагональных элементов этой матрицы.

В результате преобразований прямого хода метода Гаусса матрица А превратится в верхнюю треугольную матрицу . На главной диагонали матрицыбудут стоять единицы на всех строчках, кроме последней. А в последней строке на главной диагонали будет стоять . Поэтому определитель преобразованной матрицы будет равен (произведению диагональных элементов). В процессе прямого хода метода Гаусса используются перестановки строк, меняющие знак определителя, но не меняющие его модуль. Обозначим через s число перестановок строк, совершаемых в процессе прямого хода. Кроме того, в процессе прямого хода производятся деления строк матрицы на элементы , которые приводят к тому, что величина определителя будет разделена на произведение. Причемздесь используются значения этих величин после перестановки строк, если она производится. Таким образом, . Отсюда

. (3.2.13)

Все величины, входящие в эту формулу, кроме s, вычисляются в процессе прямого хода метода Гаусса, а вычислить величину s не составляет труда.